A brake is a device by means of which artificial frictional resistance is applied to a moving machine member, in order to retard or stop the motion of a machine. In the process of performing this function, the brake absorbs either the kinetic energy of the moving member or potential energy given up by objects being lowered by hoists, elevators, etc. In the previous articles, we discussed how we can calculate the energy absorbed by a brake and Heat Dissipation during Braking. We also discussed the different types of Brakes in the previous article. Let us discuss the Single Block Brake in detail.

As we mentioned above that the brake is used to retard or stop the motion of a machine. This action is called Braking. In the process of braking, the brake absorbs either the kinetic energy of the moving member or potential energy given up by objects being lowered by hoists, elevators etc. The energy absorbed by brakes is dissipated in the form of heat. This heat is dissipated in the surrounding air (or water which is circulated through the passages in the brake drum) so that excessive heating of the brake lining does not take place.
The design or capacity of a brake depends upon the following factors:
- The unit pressure between the braking surfaces
- The coefficient of friction between the braking surfaces
- The peripheral velocity of the brake drum
- The projected area of the friction surfaces
- The ability of the brake to dissipate heat is equivalent to the energy being absorbed.
The major functional difference between a clutch and a brake is that a clutch is used to keep the driving and driven member moving together, whereas brakes are used to stop a moving member or to control its speed.
We also solved an example problem to stop A vehicle of mass 1200 kg is moving down the hill at a slope of 1:5. by finding how much amount of Braking Torque is required to stop the vehicle in the previous article.
Single Block Brake or Single Shoe Brake
A single block or shoe brake is shown in the following figure. It consists of a block or shoe that is pressed against the rim of a revolving brake wheel drum. The block is made of a softer material than the rim of the wheel. This type of brake is commonly used on railway trains and tram cars.

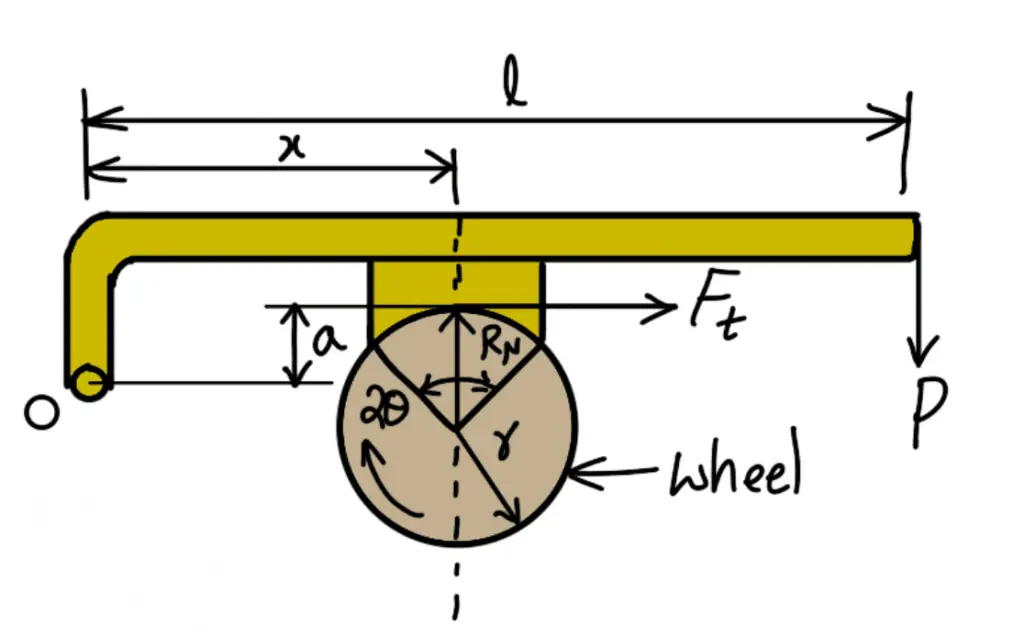
The friction between the block and the wheel causes a tangential braking force to act on the wheel, which retard the rotation of the wheel. The block is pressed against the wheel by a force applied to one end of a lever to which the block is rigidly fixed as shown in the following figure. The other end of the lever is pivoted on a fixed fulcrum O.
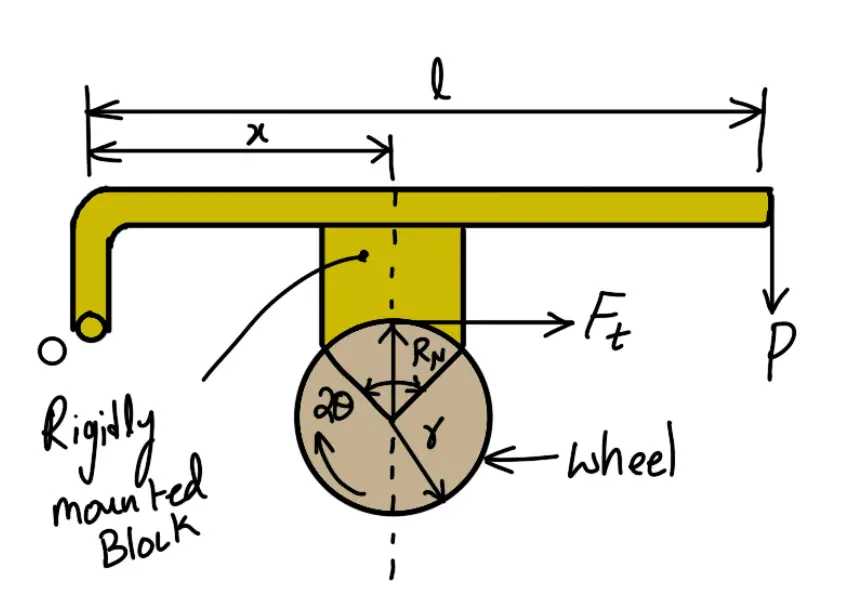
(Line of action of tangential force passes through the fulcrum of the lever.)
Let
P = Force applied at the end of the lever,
RN = Normal force pressing the brake block on the wheel,
r = Radius of the wheel
2θ = Angle of the contact surface of the block,
μ = Coefficient of friction
Ft = Tangential braking force or the frictional force acting at the contact surface of the block and the wheel.
If the angle of contact is less than 60°, then it may be assumed that the normal pressure between the block and the wheel is uniform. In such cases, tangential braking force on the wheel,
Ft = μ × RN
and the braking torque,
TB = Ft × r
TB = μ × RN × r
Let us now consider the following three cases:
- Case 1: When the line of action of tangential braking force (Ft) passes through the fulcrum O of the lever, and the brake wheel rotates clockwise, then for equilibrium, taking moments about the fulcrum O.
- Case 2: When the line of action of the tangential braking force (Ft) passes through a distance ‘a’ below the fulcrum O, and the brake wheel rotates clockwise, then for equilibrium, taking moments about the fulcrum O.
- Case 3: When the line of action of the tangential braking force passes through a distance ‘a’ above the fulcrum, and the brake wheel rotates clockwise, then for equilibrium, taking moments about the fulcrum O.
Case 1:
When the line of action of tangential braking force (Ft) passes through the fulcrum O of the lever, and the brake wheel rotates clockwise as shown in the following figure, then for equilibrium, taking moments about the fulcrum O.

(Line of action of tangential force passes through the fulcrum of the lever)
we have
RN × x = P × l
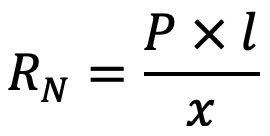
∴ Braking torque,
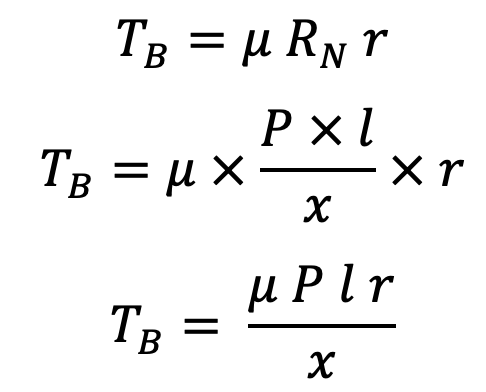
It may be noted that when the brake wheel rotates anticlockwise as shown in the following figure,
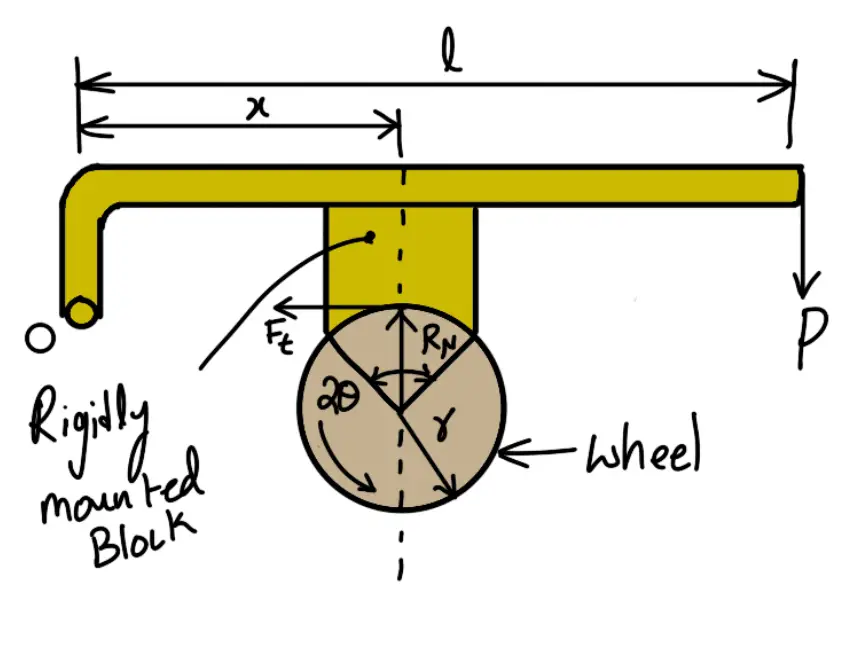
(Line of action of tangential force passes through the fulcrum of the lever)
then the braking torque is the same, i.e.
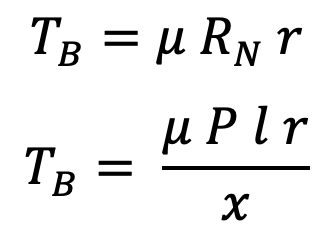
Case 2:
When the line of action of the tangential braking force (Ft) passes through a distance ‘a’ below the fulcrum O, and the brake wheel rotates clockwise as shown in the following figure,
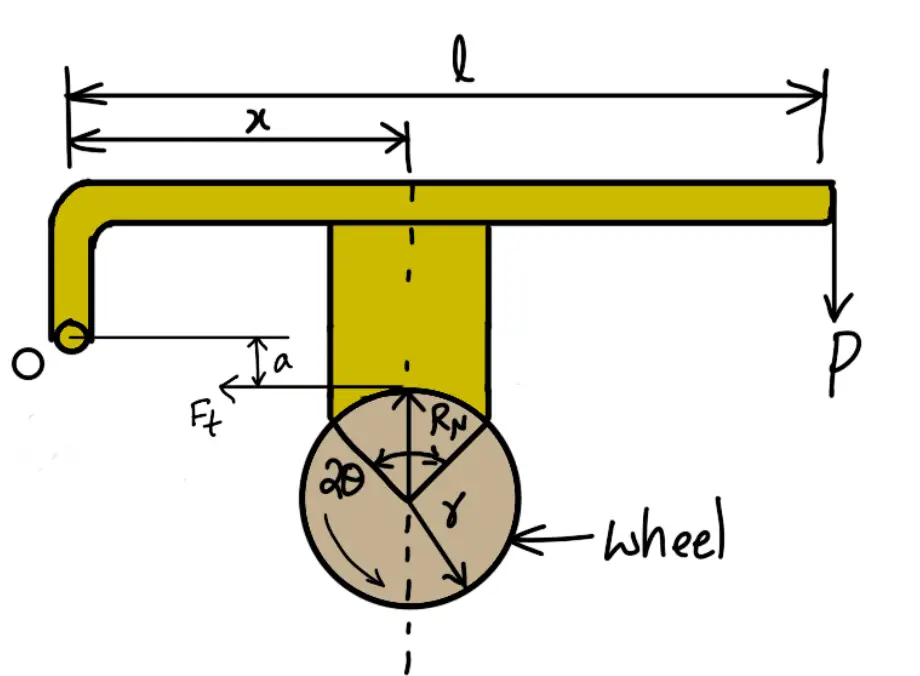
(Line of action of Ft passes below the fulcrum)
then for equilibrium, taking moments about the fulcrum O,
RN × x + Ft × a = P.l
RN × x + μ RN × a = P.l
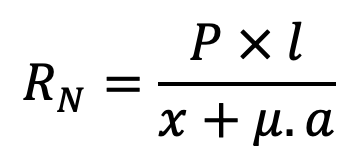
and braking torque,
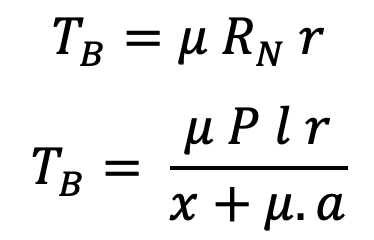
When the brake wheel rotates anticlockwise, as shown in the following figure,

(Line of action of Ft passes below the fulcrum)
then for equilibrium,
RN. x = P.l + Ft.a = P.l + μ. RN . a
…. equation (1)
RN (x – μ.a) = P.l
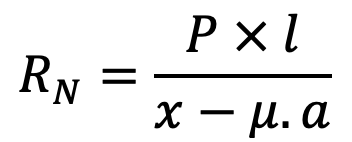
and braking torque,
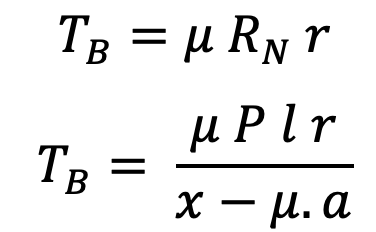
Case 3
When the line of action of the tangential braking force passes through a distance ‘a’ above the fulcrum, and the brake wheel rotates clockwise as shown in the following figure,
(Line of action of Ft passes above the fulcrum)
then for equilibrium, taking moments about the fulcrum O, we have
RN. x = P.l + Ft.a = P.l + μ.RN.a
…. equation (2)
RN (x – μ.a) = P.l
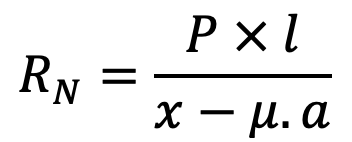
and braking torque,
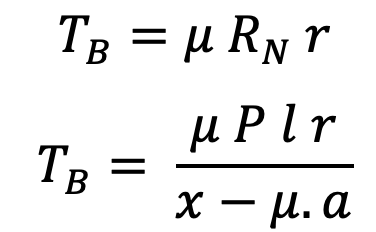
When the brake wheel rotates anticlockwise as shown in the following figure,
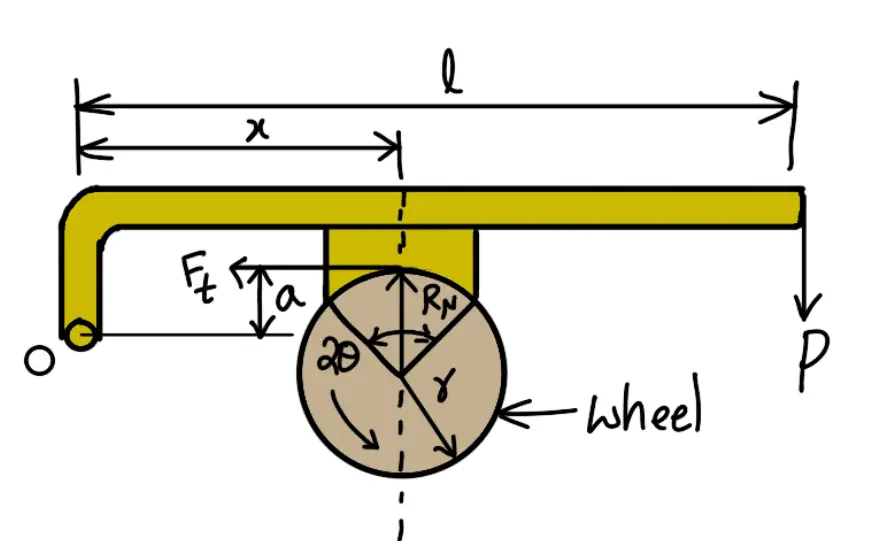
(Line of action of Ft passes above the fulcrum)
then for equilibrium, taking moments about the fulcrum O,
we have
RN × x + Ft × a = P.l
RN × x + μ.RN × a = P.l
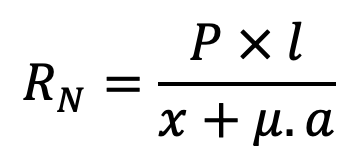
and braking torque,
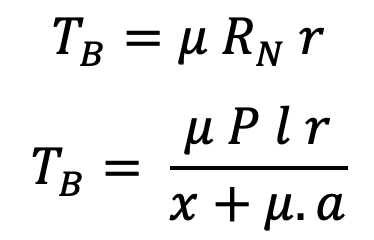
Important Notes:
- From above we see that when the brake wheel rotates anticlockwise in case 2 [figure (b)] and when it rotates clockwise in case 3 [Figure (a)], the equations (1) and (2) are the same, i.e.
RN × x = P.l + μ.RN.a
From this, we see that the moment of frictional force (μ. RN.a) adds to the moment of force (P.l). In other words, the frictional force helps to apply the brake. Such types of brakes are said to be self-energizing brakes. When the frictional force is great enough to apply the brake with no external force, then the brake is said to be a self-locking brake.
From the above expression, we see that if x ≤ μ.a, then P will be negative or equal to zero. This means no external force is needed to apply the brake and hence the brake is self-locking. Therefore the condition for the brake to be self-locking is
x ≤ μ.a
The self-locking brake is used only in back-stop applications.
- The brake should be self-energizing and not self-locking.
- In order to avoid self-locking and to prevent the brake from grabbing, x is kept greater than μ.a.
- If Ab is the projected bearing area of the block or shoe, then the bearing pressure on the shoe,
pb = RN/Ab
We know that Ab = Width of shoe × Projected length of shoe = w (2r sin θ)
- When a single block or shoe brake is applied to a rolling wheel, an additional load is thrown on the shaft bearings due to heavy normal force (RN) and produces bending of the shaft. In order to overcome this drawback, a double block or shoe brake, as discussed in this article, is used.
Pivoted Block Brake or Pivoted Shoe Brake
We have discussed in the previous article that when the angle of contact is less than 60°, then it may be assumed that the normal pressure between the block and the wheel is uniform. But when the angle of contact is greater than 60°, then the unit pressure normal to the surface of contact is less at the ends than at the center. In such cases, the block or shoe is pivoted to the lever as shown in the following figure, instead of being rigidly attached to the lever.
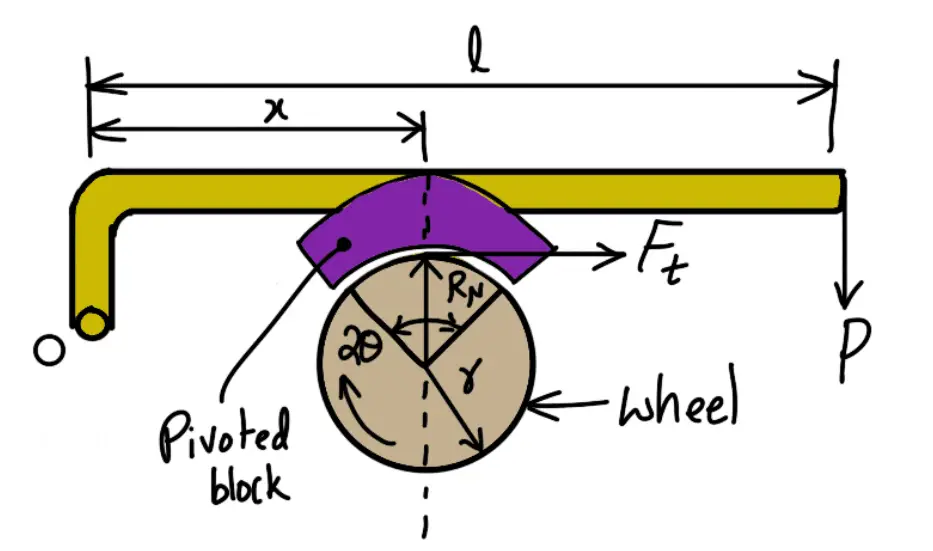
This gives uniform wear of the brake lining in the direction of the applied force. The braking torque for a pivoted block or shoe brake (i.e. when 2θ > 60°) is given by
TB = Ft × r = μ’ × RN × r
Where
μ‘ = Equivalent coefficient of friction = 4 μ sin θ ÷(2 θ + sin2θ)
μ = Actual coefficient of friction
These brakes have more life and may provide a higher braking torque.

Leave a Reply