We have already discussed what a flywheel is and its uses in the previous article. A flywheel used in machines serves as a reservoir that stores energy during the period when the supply of energy is more than the requirement and releases it during the period when the requirement of energy is more than the supply. In the case of steam engines, internal combustion engines, reciprocating compressors, and pumps, the energy is developed during one stroke and the engine is to run for the whole cycle on the energy produced during this one stroke. Let us discuss the Different stresses in a Flywheel Rim.

Stresses in a Flywheel Rim
A flywheel, as shown in the following figure, consists of a rim at which the major portion of the mass or weight of the flywheel is concentrated, a boss or hub for fixing the flywheel onto the shaft, and a number of arms for supporting the rim on the hub.
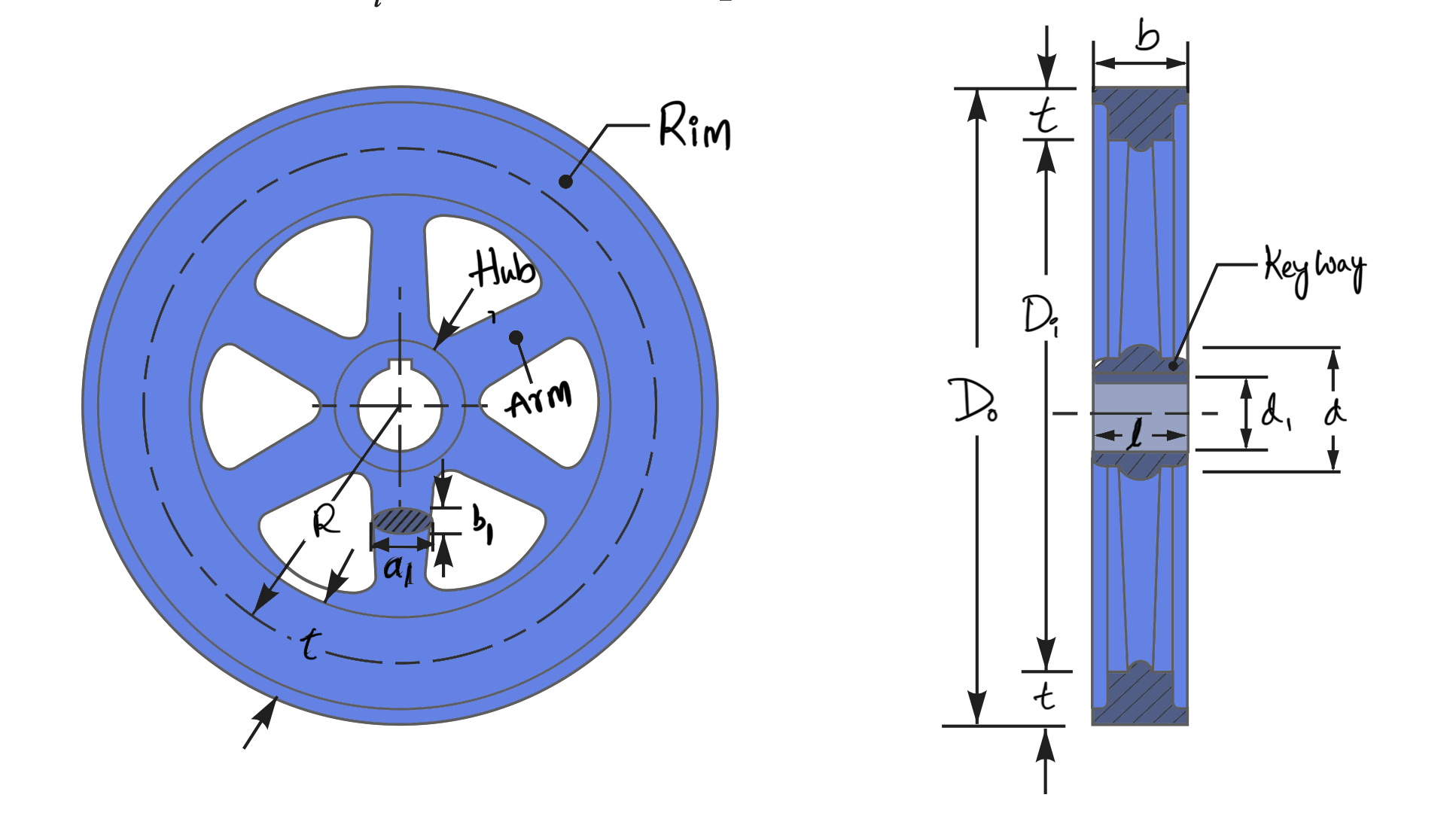
The following types of stresses are induced in the rim of a flywheel:
- Tensile stress due to centrifugal force
- Tensile bending stress caused by the restraint of the arms
- The shrinkage stresses are due to the unequal rate of cooling of casting. These stresses may be very high but there is no easy method of determining. This stress is taken care of by a factor of safety.
We only discussed the first two types of stresses as follows:
1. Tensile stress due to the centrifugal force
The tensile stress in the rim due to the centrifugal force, assuming that the rim is unstrained by the arms, is determined in a similar way as a thin cylinder subjected to internal pressure.
Let
b = Width of rim
t = Thickness of rim
A = Cross-sectional area of rim = b × t
D = Mean diameter of the flywheel
R = Mean radius of flywheel
ρ = Density of flywheel material
ω = Angular speed of flywheel
v = Linear velocity of flywheel
σt = Tensile or hoop stress
Consider a small element(shaded) of the rim as shown in the following figure. Let it subtend an angle δθ at the center of the flywheel.
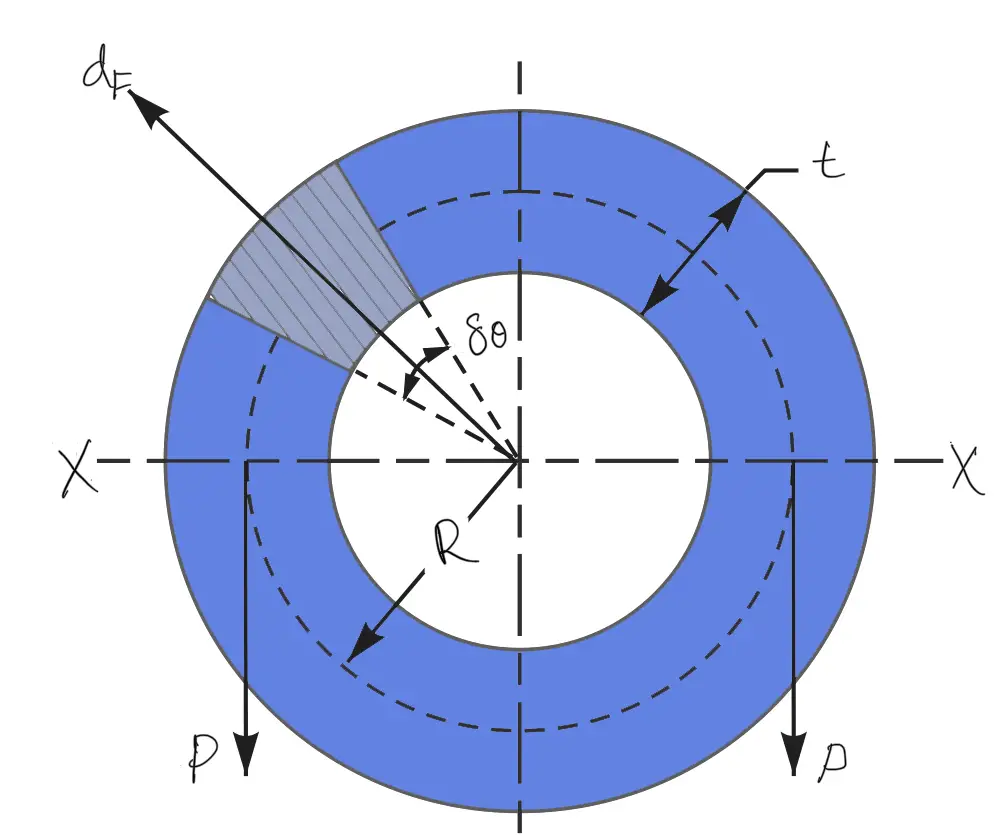
The volume of the small element = A.R.δθ
∴ Mass of the small element dm = Volume × Density
dm = A.R.δθ.ρ
dm = ρ.A.R.δθ
and centrifugal force on the element,
dF = dm.ω2.R
dF = ρ.A.R.δθ.ω2.R
dF = ρ.A.R2.ω2.δθ
The vertical component of dF = dF sin θ = ρ.A.R2.ω2.δθ sin θ
Total vertical bursting force across the rim diameter X-Y = ρ.A.R2.ω2 0∫π sinθ dθ
= ρ.A.R2.ω2 [– cos θ]0π
= 2 ρ.A.R2.ω2
This vertical force is resisted by a force of 2P, such that
2P = 2σt × A
From the above two equations, we have
2 ρ.A.R2.ω2 = 2σt × A
σt = ρ.R2.ω2
σt = ρ.v2
(∴ v = ω.R)
when ρ is in kg/m3 and v is in m/s, then σt will be in N/m2 or Pa.
From the above expression, the mean diameter (D) of the flywheel may be obtained by using the relation,
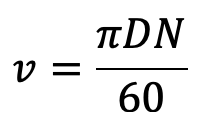
2. Tensile bending stress caused by restraint of the arms
The tensile bending stress in the rim due to the restraint of the arms is based on the assumption that each portion of the rim between a pair of arms behaves like a beam fixed at both ends and uniformly loaded, as shown in the following figure, such that the length between fixed ends,
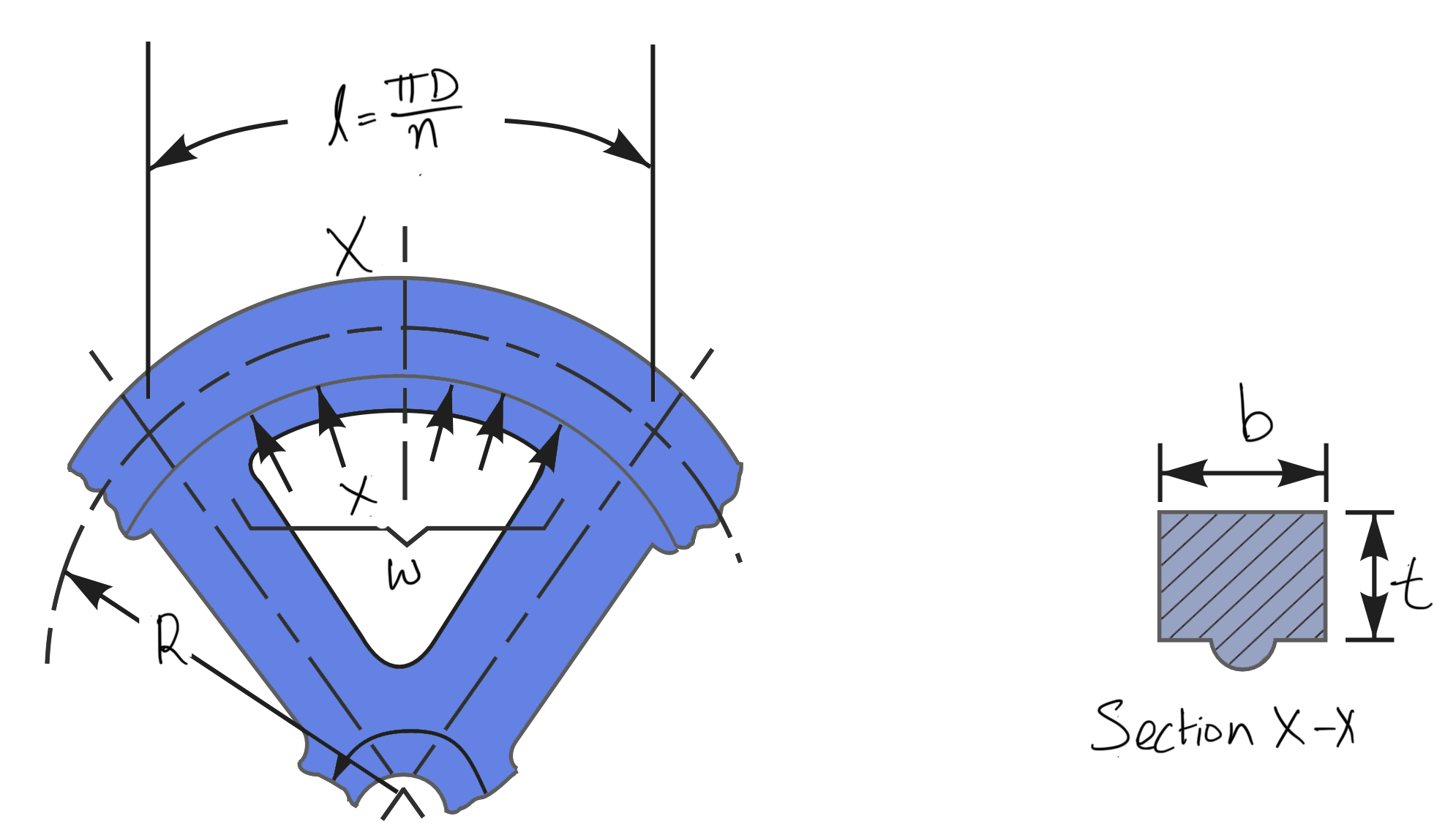
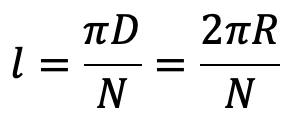
where n = Number of arms.
The uniformly distributed load (w) per meter length will be equal to the centrifugal force between a pair of arms.
w = b.t.ρ.ω2.R N/m
We know that the maximum bending moment,
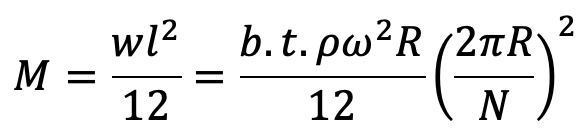
and section modulus,
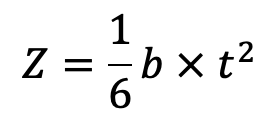
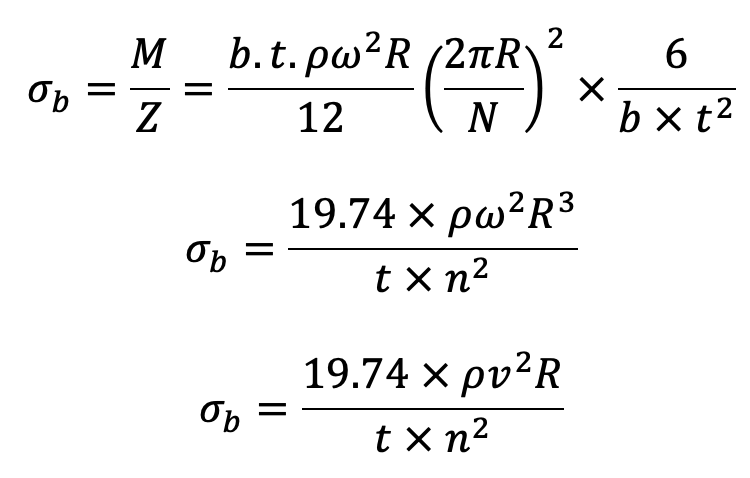
Now total stress in the rim σ = σt + σb
If the arms of a flywheel do not stretch at all and are placed very close together, then centrifugal force will not set up stress in the rim. In other words, σt will be zero. On the other hand, if the arms are stretched enough to allow free expansion of the rim due to centrifugal action, there will be no restraint due to the arms, i.e. σb will be zero.
It has been shown by G. Lanza that the arms of a flywheel stretch about 3/4 th of the amount necessary for free expansion. Therefore the total stress in the rim,
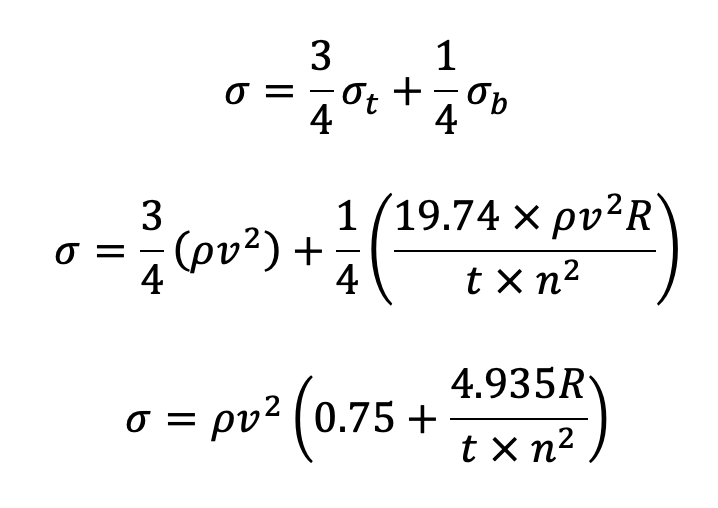
With these relations we can find the maximum stresses in a Flywheel Rim. Let us know what you think about this article in the comment section below.

Leave a Reply