The Flywheel, so-called the Energy reservoir also some times referred to as the inertia ring. This is used to store the energy during the period when the supply of energy is more than the required and utilise it during the period when it is less than the required in the cyclic operation.

Flywheel
In the case of reciprocating compressors, Internal combustion engines and steam engines the energy is developed during the one power stroke and the engine has to complete the remaining strokes in the cycle with this energy generated by the power stroke.
For Example, in the case of a Four-stroke Internal combustion Engines, There will be one power stroke for the two rotation of the crank. The energy developed during the power stroke is more than the load and there is no energy developed during the remaining strokes (Suction, Compression, Expansion).

So A flywheel is mounted to absorb the energy during the power stroke and release during the remaining strokes.
Generally, during the power stroke, the crank speed will increase and during the other strokes, this speed will be reduced. This fluctuation of speed can be reduced with this flywheel.
Coefficient of fluctuation speed
The difference between the max. engine speed to the min. engine speed during the cycle is called the fluctuation speed. The ratio of the max. speed to the min. speed is called the Coefficient of Fluctuation of Speed.
The mean speed N = (N1+N2)/2
where N1 and N2 maximum and minimum speeds during the thermodynamic cycle
∴ Coefficient of fluctuation of speed in terms of speed (rpm)
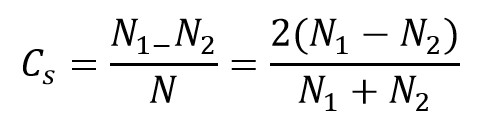
∴ Coefficient of fluctuation of speed in terms of angular speed
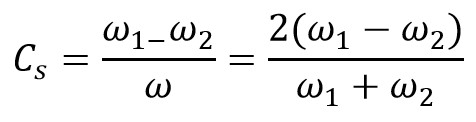
∴ Coefficient of fluctuation of speed in terms of linear velocity
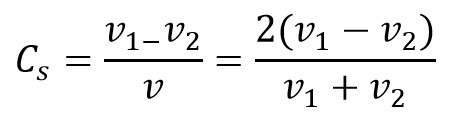
The coefficient of fluctuation of speed is a limiting factor in the design of flywheel.
Likewise, we can also calculate the energy stored in the flywheel with the following derivation.
Energy Stored in Flywheel
Consider a flywheel of rim radius R as shown in the following diagram. Whose mass is m and k is the radius of gyration and I is the mass moment of inertia about its axis of rotation. (Check this Mass Moment of Inertia Calculator to calculate the Flywheel inertia. It will be fun)
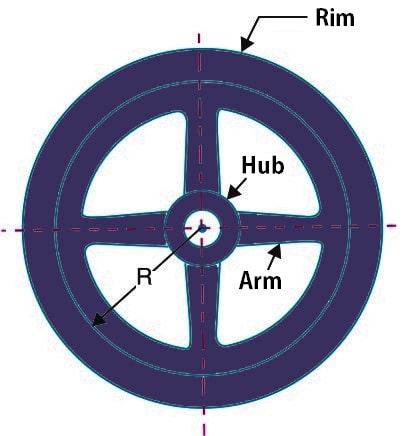
as we have already mentioned above N1 and N2 maximum and minimum speeds during the thermodynamic cycle. likewise, ω1 and ω2 are the angular speeds.
The mean kinetic energy of the flywheel can be written as
E = (I × ω2 )/2
E = ( m × k2 × ω2 )/2
Units in Joules or N-m
A little consideration will be taken that the gyration k will also be considered as same as the R the radius flywheel rim.
Since the flywheel speed changes from ω1 to ω2,
ΔE = Maximum kinetic energy of the flywheel – Minimum Kinetic energy of the flywheel
ΔE = (I × (ω1)2)/2 – (I × (ω2)2)/2
ΔE = I ×[ (ω1)2 -(ω2)2)]/2 =
ΔE = I ×[(ω1 + ω2)(ω1 – ω2)]/2
From the mean angular speed equation, we can write
ΔE = I × ω(ω1 – ω2)
from the Coefficient of fluctuation of speed in terms of angular speed equation, we can write
ΔE = I × ω2 × CS
From the flywheel kinetic energy equation, we can also write the following.
ΔE = 2E CS (Joules or N-m)
This above equation represents the energy stored in the flywheel.
Conclusion
We have discussed what is the flywheel and how it is helpful as the energy storage in the reciprocating and diesel engines. Also derived the formulas to calculate the energy stored in the flywheel and the fluctuation speed coefficient. If you have any further thoughts on this topic, let us know in the comment section below.

Leave a Reply