Different Stresses in a Flywheel Arms

We have already discussed what a flywheel is and its uses. A flywheel used in machines serves as a reservoir that stores energy during the period when the supply of energy is more than the requirement and releases it during the period when the requirement of energy is more than the supply. In the case of steam engines, internal combustion engines, reciprocating compressors, and pumps, the energy is developed during one stroke and the engine is to run for the whole cycle on the energy produced during this one stroke. In the previous article we have discussed the Different stresses in a Flywheel Rim. Let us discuss the Different stresses in a Flywheel Arms.

Stresses in Flywheel Arms

The following stresses are induced in the arms of a flywheel.

1. Tensile stress due to centrifugal force acting on the rim.
2. Bending stress due to the torque transmitted from the rim to the shaft or from the shaft to the rim.
3. Shrinkage stresses due to unequal rate of cooling of casting. These stresses are difficult to determine. This stress is taken care of by a factor of safety.

We only discussed the first two types of stresses as follows:

1. Tensile stress due to the centrifugal force

Due to the centrifugal force acting on the rim, the arms will be subjected to direct tensile stress whose magnitude is same as discussed in the previous article.

Tensile stress in the arms,

σ_t1 = 3/4 & σ_t = 3/4 ρ × v²

2. Bending stress due to the torque transmitted

Due to the torque transmitted from the rim to the shaft or from the shaft to the rim, the arms will be subjected to bending, because they are required to carry the full torque load. In order to find out the maximum bending moment on the arms, it may be assumed as a centilever beam fixed at the hub and carrying a concentrated load at the free end of the rim as shown in the following figure.

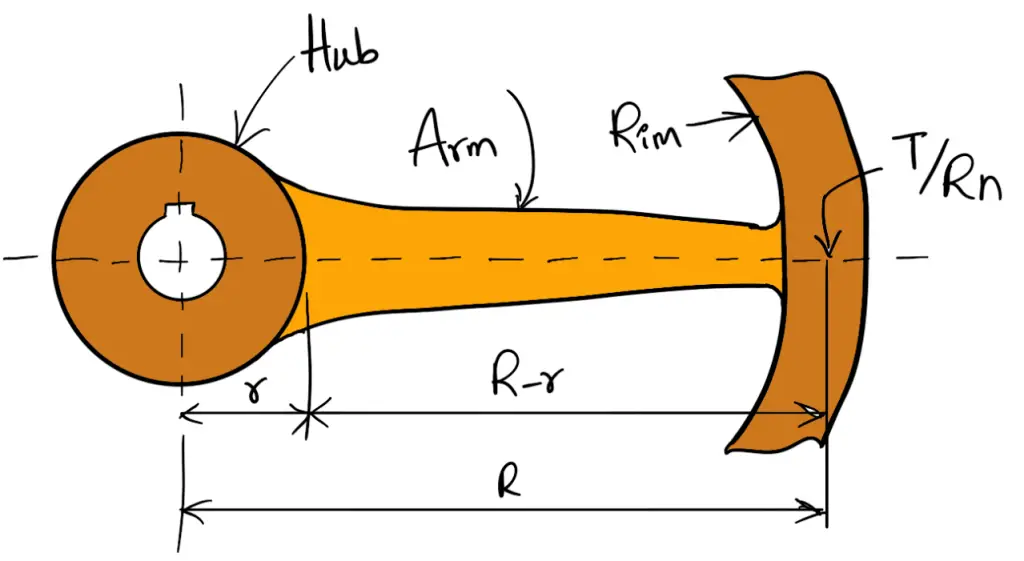
Let
T = Maximum torque transmitted by the shaft
R = Mean radius of the rim
r = Radius of the hub
n = Number of arms
Z = Section modulus for the cross-section of arms

We know that the load at the mean radius of the rim,

F = T/R

∴ Load on each arm = T / (R × n)

and maximum bending moment which lies on the arm at the hub,

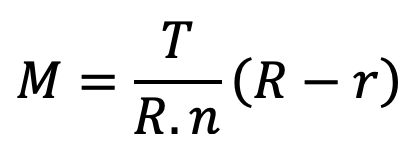
∴ Bending stress in arms,

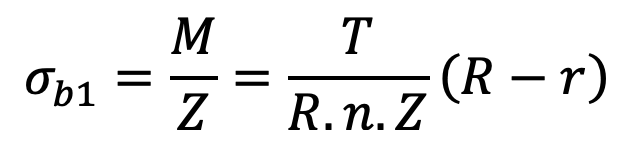
∴ Total tensile stress in the arms at the hub end,

σ = σ_t + σ_b

👉Important Notes:
1. The total stress on the arms should not exceed the allowable permissible stress.
2. If the flywheel is used as a belt pulley, then the arms are also subjected to bending due to net belt tension (T₁ – T₂), where T₁ and T₂ are the tensions in the tight side and slack side of the belt respectively. Therefore the bending stress due to the belt tensions,

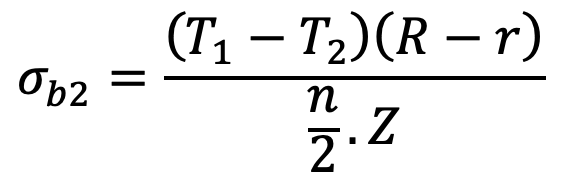
(∵ Only half the number of arms are considered to be effective in transmitting the belt tensions)

∴ Total bending stress in the arms at the hub end,

σ_b = σ_b1 + σ_b2

and the total tensile stress in the arms at the hub end,

σ = σ_t1 + σ_b1 + σ_b2

With these relations we can find the maximum stresses in a Flywheel arm. Let us know what you think about this article in the comment section below.