Design of Leaf Springs with Example Problem

A spring is defined as an elastic body, whose function is to distort when loaded and to recover its original shape when the load is removed. It absorbs or controls energy due to either shock or vibration so it can be used as shock absorbers and vibration dampers. It is also used to apply forces, as in brakes, clutches, and spring-loaded valves. We have already discussed different types of springs and also about the leaf springs in detail. Let us discuss the Design of Leaf Springs with an Example Problem.

Leaf Spring

The laminated or leaf spring (also known as flat spring or carriage spring) consists of a number of flat plates (known as leaves) of varying lengths held together by means of clamps and bolts. These are mostly used in automobiles. The advantage of a leaf spring over a helical spring is that the ends of the spring may be guided along a definite path as it deflects to act as a structural member in addition to an energy-absorbing device. Thus the leaf springs may carry lateral loads, brake torque, driving torque, etc., in addition to shocks.

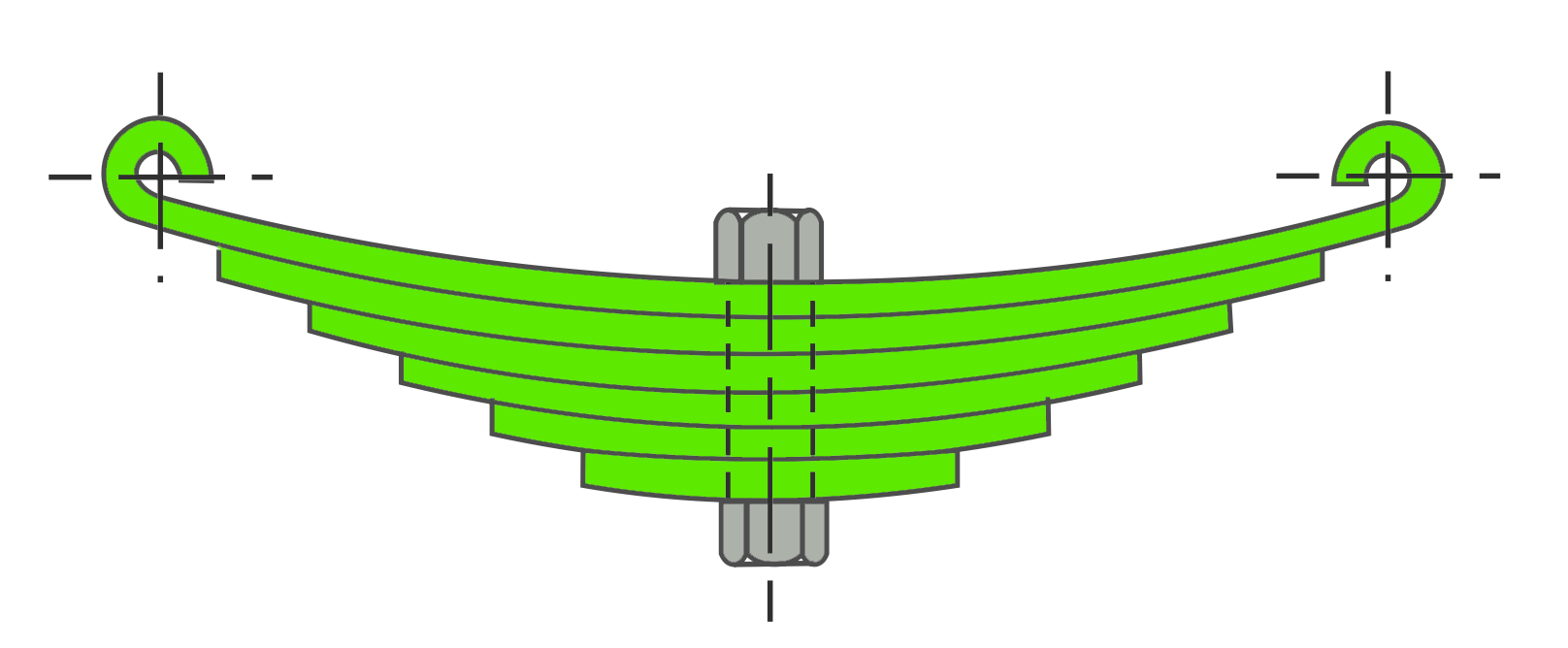
Design of Leaf Springs with Example Problem

Problem Statement: A semi-elliptical laminated vehicle spring to carry a load of 6000 N is to consist of seven leaves 65 mm wide, two of the leaves extending the full length of the spring. The spring is to be 1.1 m in length and attached to the axle by two U-bolts 80 mm apart. The bolts hold the central portion of the spring so rigidly that they may be considered equivalent to a band having a width equal to the distance between the bolts. Assume a design stress for spring material as 350 MPa. Determine :

1. Thickness of leaves,
2. Deflection of spring,
3. Diameter of eye,
4. Length of leaves
5. Radius to which leaves should be initially bent.

Note: The standard thickness of leaves are : 5, 6, 6.5, 7, 7.5, 8, 9, 10, 11 etc. in mm.

Answer:

Given data:
Load 2W = 6000N or W = 3000N
Number of leaves n=7
width of leaves b = 65mm
Number of full-length leaves n_F =2
Length of spring 2L₁ = 1.1m = 1100mm or L₁ = 550mm
U-bolts distance l = 80mm
Design Stress σ = 350MPa = 350 N/mm²

1. Thickness of leaves

Let
t = Thickness of leaves.

We know that the effective length of the spring,

2L = 2L₁ – l = 1100 – 80 = 1020mm
∴ L = 1020 / 2 = 510 mm

and number of graduated leaves,

n_G = n–n_F = 7–2 = 5

Assuming that the leaves are not initially stressed, the maximum stress (σ_F),

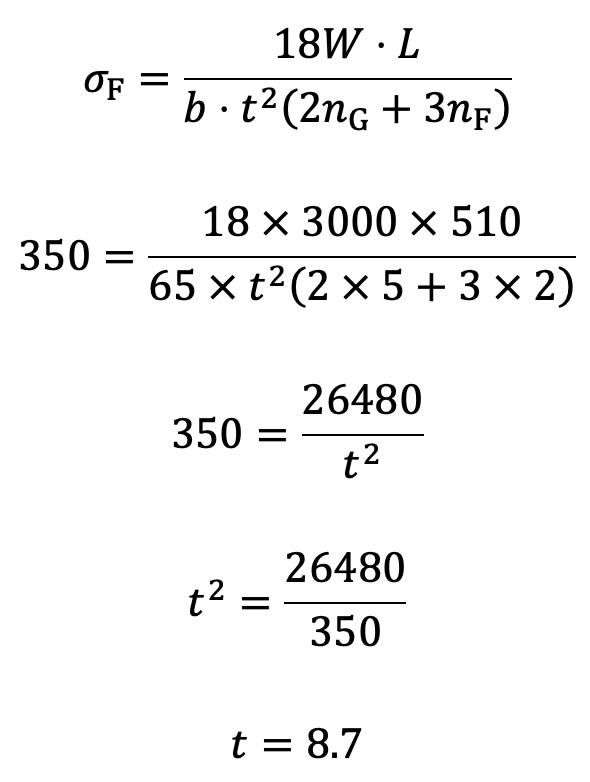
Let us say the thickness of the leaves is 9mm.

2. Deflection of spring

We know that the deflection of spring,

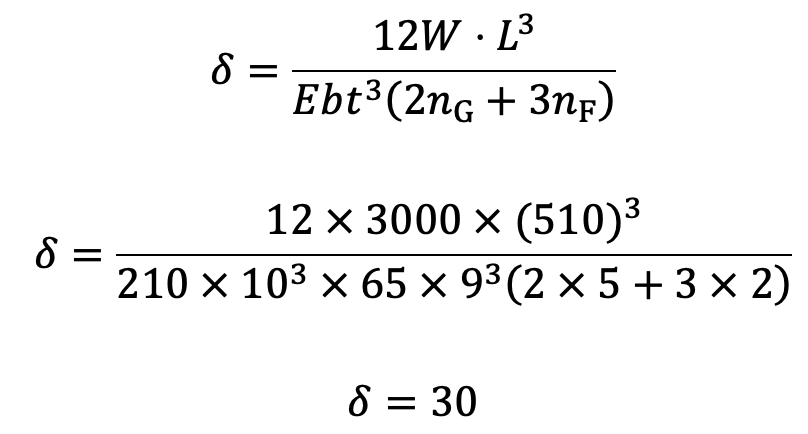
The deflection of the spring is 30mm.

3. Diameter of eye

The inner diameter of the eye is obtained by considering the pin in the eye in bearing because the inner diameter of the eye is equal to the diameter of the pin.

Let
d = Inner diameter of the eye or diameter of the pin,
l₁ = Length of the pin which is equal to the width of the eye or leaf (i.e. b) = 65 mm …(Given)
p_b = Bearing pressure on the pin which may be taken as 8 N/mm².

We know that the load on pin (W),

3000 = d × l₁ × p_b
3000 = d×65×8=520d
d = 3000 / 520
d = 5.77

Let us say the Diameter of the eye is 6mm.

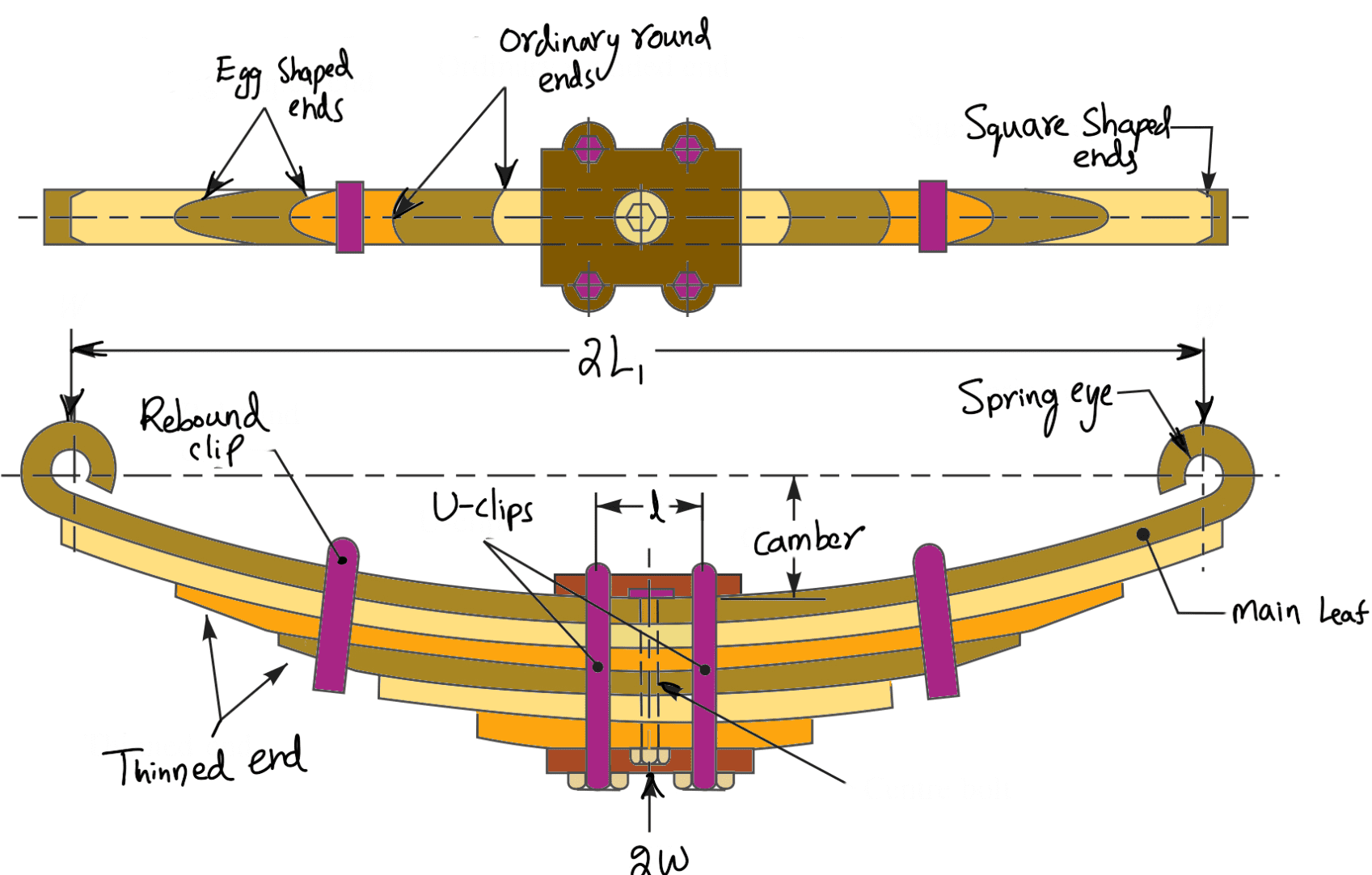
Let us now consider the bending of the pin. Since there is a clearance of about 2 mm between the shackle (or plate) and eye as shown in the following figure, therefore length of the pin under bending,

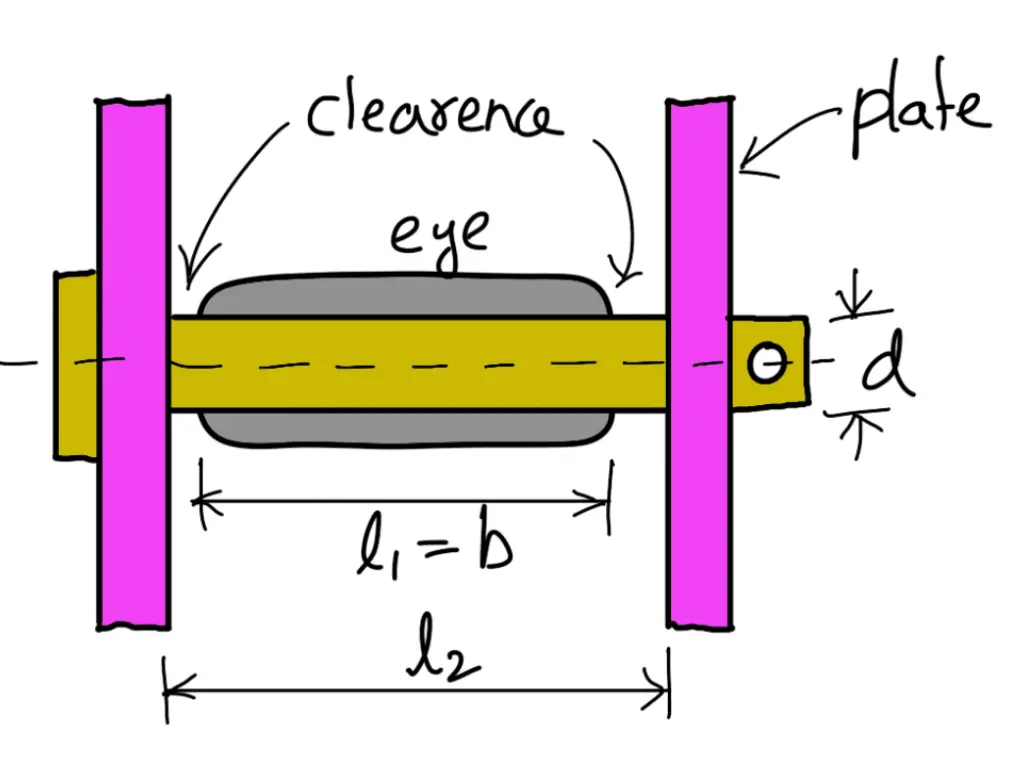
l₂ = l₁ + 2 × 2 = 65 + 4 = 69mm

Maximum bending moment on the pin,

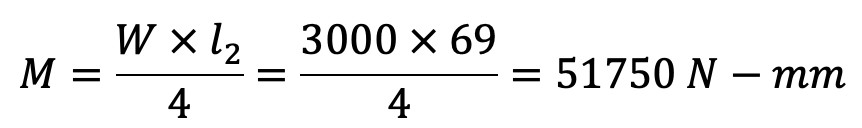
and section modulus,

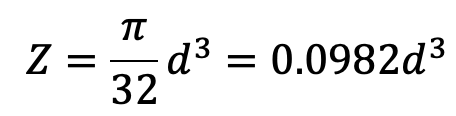
We know that bending stress (σ_b),

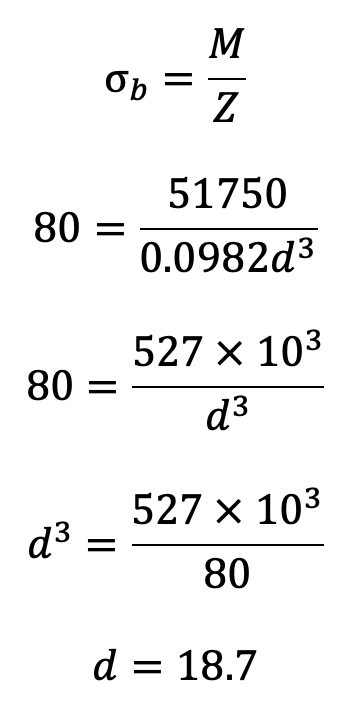
We shall take the inner diameter of the eye or diameter of pin (d ) as 20 mm

Let us now check the pin for induced shear stress. Since the pin is in double shear, therefore load on the pin (W ),

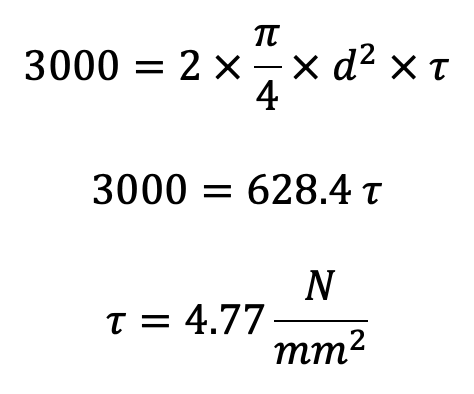
4. Length of leaves

We know that the ineffective length of the spring = l = 80 mm

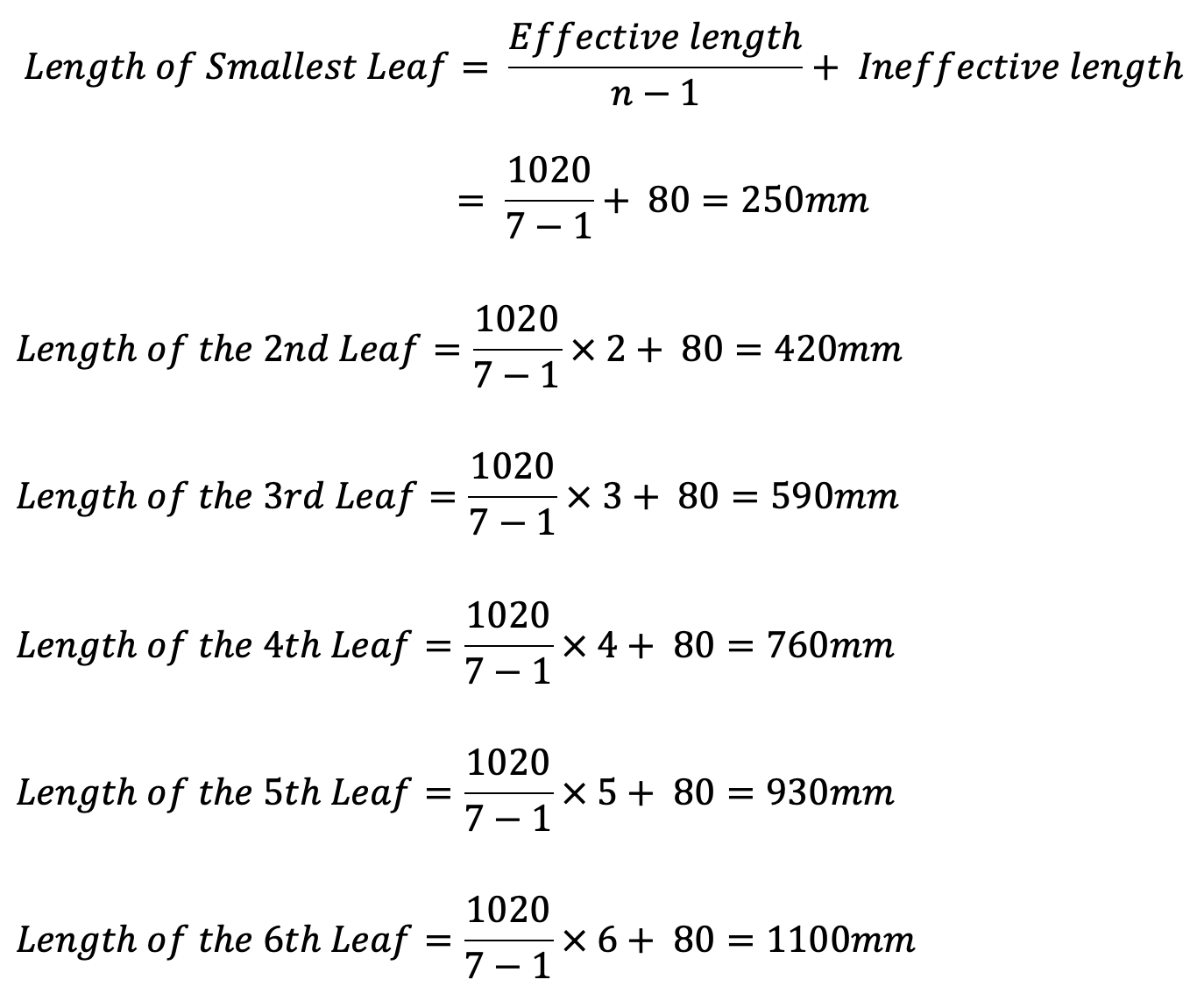
The 6th and 7th leaves are full-length leaves and the 7th leaf (i.e. the top leaf) will act as a master leaf.

We know that the length of the master leaf

= 2L₁ + π (d + t) 2
= 1100 + π (20 +9) 2
= 1282.2 mm

5. Radius to which the leaves should be initially bent

Let
R = Radius to which the leaves should be initially bent
y = Camber of the spring.

We know that

y (2R – y) = (L₁)²
30 (2R – 30) = (550)²
2R – 30 = (550)²/ 30
2R – 30 = 10083
R = (10083-30)/2
R = 5056.5

The radius to which the leaves should be initially bent is 5056.5mm.

This is all about the Design of Leaf Springs with an Example Problem for an automobile vehicle. Let us know what you think about this article in the comment section below.