In the Previous article, we have discussed different types of keys for shafts, Now we are going to discuss what are the different types of forces acting on Key, and the design of Key for the shaft.

Different forces acting on the Keys

First of all, we have to know what are the different types of the forces acting on the keys.

When a key is used in the Mechanical equipment for the torque transmission from a motor shaft to the equipment (Compressor/Pump/Gearbox) end, they will be connected by a coupling with the help of hubs having keys in it to the motor shaft. In this situation, the Key is subjected to the following forces

1. Force due to the type of fit in its keyway
2. Force Due to the torque transmitting by the shaft

1.Force due to the type of fit in its keyway (F1)

Force due to the type of fit in its keyway results in compressive stresses in the key which are difficult to determine in the magnitude.

2.Force Due to the torque transmitting by the shaft (F)

Force Due to the torque transmitting by the shaft results in shearing stress and the Compressive(Crushing) stress.

These stresses cannot be uniform along the length of the key, due to the forces which are concentrated on the torque input end on the shaft to the hub thru the key.

The stresses due to the Type of fit are considerably neglected and assumed to be they are uniform along the length of the key.

Design of Key for Shaft

Consider a Parallel Sunk key of width w, Height h, of length l, is connecting a shaft and the hub as shown in the figure.

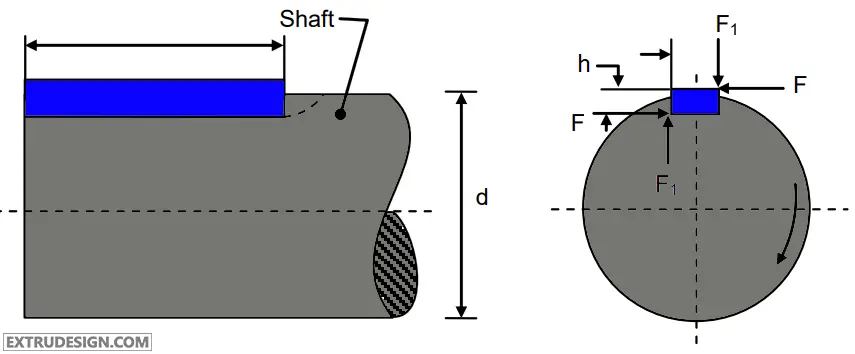
Where

T = Torque transmitted by the shaft,

F = Tangential force acting at the circumference of the shaft,

d = Diameter of the shaft,

w = Width of the key,

h= Height of the key,

l = Length of the key.

τ  = Shear Stress for the material of the Key

σ_c = Crushing stresses for the material of the key

So the total torque transmitted by the shaft (T) = F × d/2       (Eqn 1)

The Tangential force acting on the key at the two places as you can see in the above schematic diagram.

a. Tangential Shearing force.

b. Tangential crushing force.

The tangential Shearing force F = Area resisting shearing force × Shear stress      …….. ( From Shear stress formula)

F = l×w×τ      (Eqn 2)

The tangential crushing force F = Area resisting crushing × Crushing stress     ………….. ( From Compressive (Crushing) stress Formula)

F = l×(h/2)×σ_c     (Eqn 3)

 

The key is equally strong in shearing and the Crushing so,

From the Eqn 1, Eqn 2, Eqn 3, we can write

l×w×τ×(d/2) = l×(h/2)×σ_c×(d/2)

w/h = σ_c/2τ       (Eqn 4)

This equation means The permissible crushing stress for the usual key material should be at least twice as the permissible sharing stress.

If we have The permissible crushing stress = 2× permissible sharing stress then

from the Eqn 4, we can write

w = h

This means a square key is equally strong in both shearing and the crushing.

In order to find out the length of the key to transmit the full power of the shaft, the shearing strength of the key should be equal to the torsional shear strength of the shaft.

From the above equation, the shearing strength of the key is(From Eqn1 and Eqn 2) T =  l×w×τ × d/2         …………(Eqn 5)

We know the torsional shear strength of the shaft is T = (π/16)×τ₁×d³                     ……… (Eqn 6)

( ∴Where τ₁ = Shear stress for the shaft material.)

From the above statement, shearing strength of the key = the torsional shear strength of the shaft.

we can write from Eqn 5 and Eqn 6

l×w×τ × d/2 = (π/16)×τ₁×d³ 

From the above equation evaluate l 

l = 1.571×d×(τ_1/τ)

Here if the material of the key is as same as the shaft material then τ₁ = τ 

then

l = 1.571×d

We have to maintain the length of the key at 1.571 times to the diameter of the shaft.

Conclusion

We have discussed how the design of the key should be to transmit the full power of the shaft. Please let us know your thoughts about this article in the below comments section.