A clutch is a machine member used to connect a driving shaft to a driven shaft so that the driven shaft may be started or stopped at will, without stopping the driving shaft. The use of a clutch is mostly found in automobiles. In the previous article, we have briefed about the different types of clutches. Let us see the Design of a Disc Clutch or a plate clutch.

Clutch
A clutch is a machine member used to connect a driving shaft to a driven shaft so that the driven shaft may be started or stopped at will, without stopping the driving shaft. The use of a clutch is mostly found in automobiles. A little consideration will show that in order to change gears or to stop the vehicle, it is required that the driven shaft should stop, but the engine should continue to run. It is, therefore, necessary that the driven shaft should be disengaged from the driving shaft. The engagement and disengagement of the shafts is obtained by means of a clutch which is operated by a lever.
Disc Clutch | Plate Clutch
A disc or plate clutch is a type of friction clutch. A friction clutch has its principal application in the transmission of power of shafts and machines which must be started and stopped frequently. Its application is also found in cases in which power is to be delivered to machines partially or fully loaded. The force of friction is used to start the driven shaft from rest and gradually bring it up to the proper speed without excessive slipping of the friction surfaces. In automobiles, a friction clutch is used to connect the engine to the drive shaft.
In operating such a clutch, care should be taken so that the friction surfaces engage easily and gradually bring the driven shaft up to proper speed. The proper alignment of the bearing must be maintained and it should be located as close to the clutch as possible.
It may be noted that:
- The contact surfaces should develop a frictional force that may pick up and hold the load with reasonably low pressure between the contact surfaces.
- The heat of friction should be rapidly dissipated and the tendency to grab should be at a minimum.
- The surfaces should be backed by a material stiff enough to ensure a reasonably uniform distribution of pressure.
During the operation of a clutch, most of the work done against frictional forces opposing the motion is liberated as heat at the interface. It has been found that at the actual point of contact, a temperature as high as 1000°C is reached for a very short duration (i.e. for 0.0001 seconds). Due to this, the temperature of the contact surfaces will increase and may destroy the clutch.
Single Disc or Plate Clutch
A single disc or plate clutch, as shown in the following schematic diagram, consists of a clutch plate whose both sides are faced with a frictional material (usually of Ferrodo). It is mounted on the hub which is free to move axially along the splines of the driven shaft. The pressure plate is mounted inside the clutch body which is bolted to the flywheel.
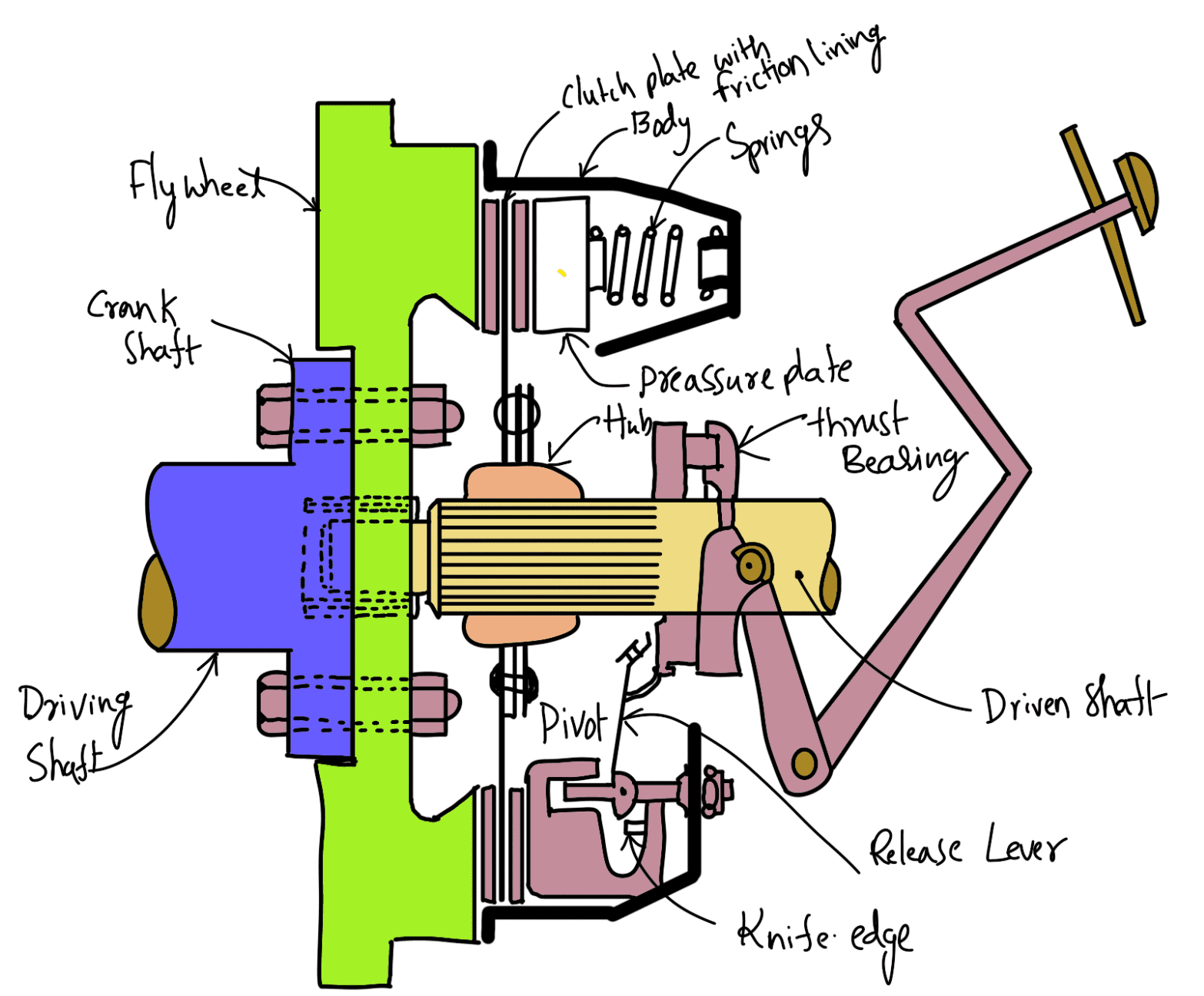
Both the pressure plate and the flywheel rotate with the engine crankshaft or the driving shaft. The pressure plate pushes the clutch plate towards the flywheel by a set of strong springs which are arranged radially inside the body. The three levers (also known as release levers or fingers) are carried on pivots suspended from the case of the body.
These are arranged in such a manner that the pressure plate moves away from the flywheel by the inward movement of a thrust bearing. The bearing is mounted upon a forked shaft and moves forward when the clutch pedal is pressed.
When the clutch pedal is pressed down, its linkage forces the thrust release bearing to move in towards the flywheel and press the longer ends of the levers inward. The levers are forced to turn on their suspended pivot and the pressure plate moves away from the flywheel by the knife edges, thereby compressing the clutch springs.

This action removes the pressure from the clutch plate and thus moves back from the flywheel and the driven shaft becomes stationary. On the other hand, when the foot is taken off from the clutch pedal, the thrust bearing moves back by the levers. This allows the springs to extend and thus the pressure plate pushes the clutch plate back towards the flywheel.
The axial pressure exerted by the spring provides a frictional force in the circumferential direction when the relative motion between the driving and driven members tends to take place. If the torque due to this frictional force exceeds the torque to be transmitted, then no slipping takes place and the power is transmitted from the driving shaft to the driven shaft.
Design of a Disc Clutch or Plate Clutch
Consider two friction surfaces maintained in contact by an axial thrust (W ) as shown in the following figure (left).
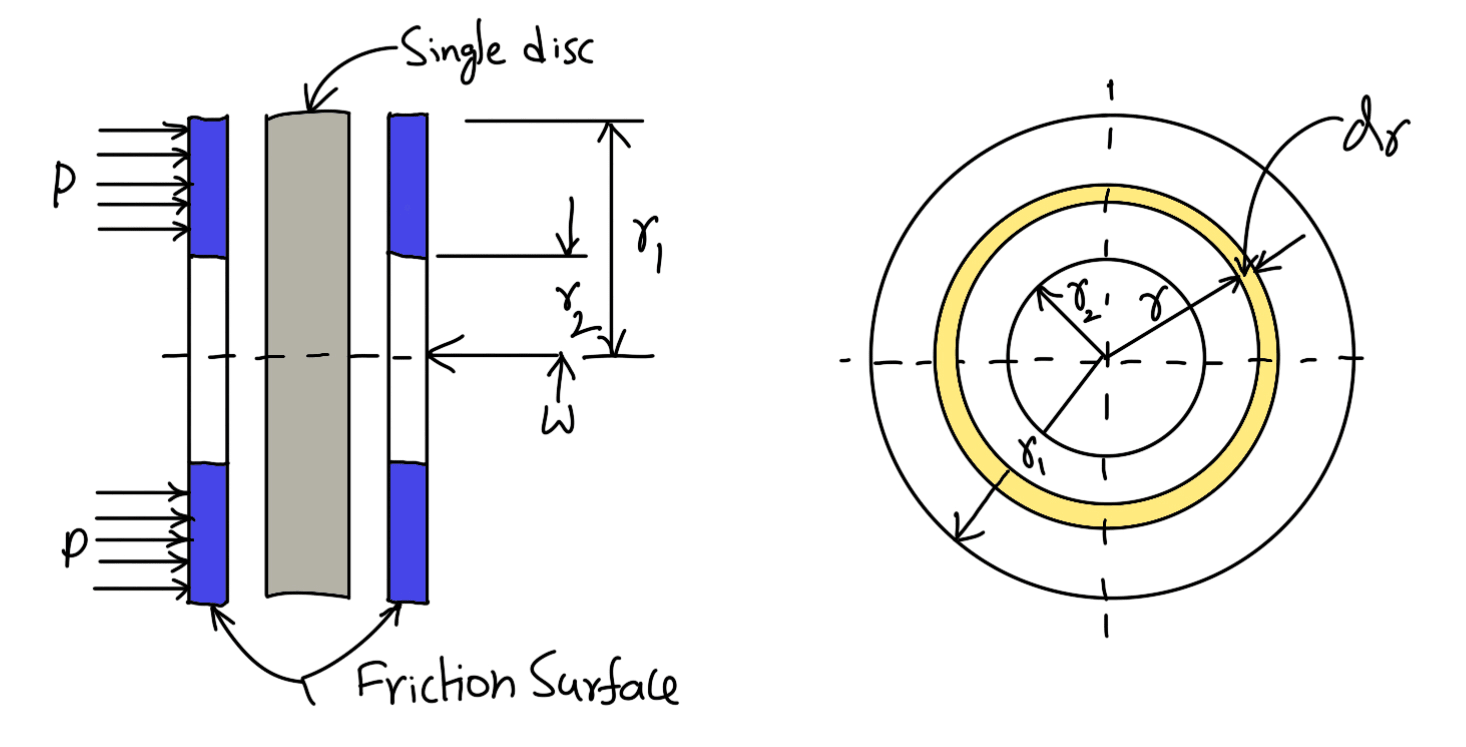
(Design of a Disc Clutch)
Let
T = Torque transmitted by the clutch,
p = Intensity of axial pressure with which the contact surfaces are held together,
r1 and r2 = External and internal radii of friction faces,
r = Mean radius of the friction face
μ = Coefficient of friction
Consider an elementary ring of radius r and thickness dr as shown in the above figure (right). We know that the area of the contact surface or friction surface
Normal or axial force on the ring,
δW = Pressure × Area = p × 2πr.dr
and the frictional force on the ring acting tangentially at radius r,
Fr = μ × δW = μ.p × 2πr.dr
∴ Frictional torque acting on the ring,
Tr = Fr × r = μ . p × 2πr.dr × r = 2πμp.r2.dr
We shall now consider the following two cases :
- When there is a uniform pressure
- When there is uniform axial wear
Considering uniform pressure
hen the pressure is uniformly distributed over the entire area of the friction face as shown in the above figure (left), then the intensity of pressure,
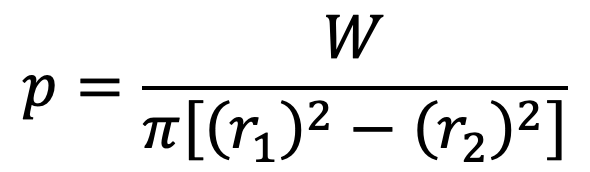
where
W = Axial thrust with which the friction surfaces are held together.
We have discussed above that the frictional torque on the elementary ring of radius r and thickness dr is
Tr = 2π μ.p.r2.dr
Integrating this equation within the limits from r2 to r1 for the total friction torque.
Total frictional torque acting on the friction surface or on the clutch,

where
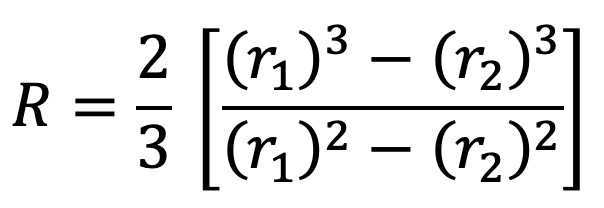
Considering uniform axial wear
The basic principle in designing machine parts that are subjected to wear due to sliding friction is that normal wear is proportional to the work of friction. The work of friction is proportional to the product of normal pressure ( p) and the sliding velocity (V). Therefore,
Normal wear ∝ Work of friction ∝ p.V
p.V = K (a constant)
or
p = K/V
It may be noted that when the friction surface is new, there is a uniform pressure distribution over the entire contact surface. This pressure will wear most rapidly where the sliding velocity is maximum and this will reduce the pressure between the friction surfaces. This wearing-in process continues until the product p.V is constant over the entire surface. After this, the wear will be uniform as shown in the following figure.
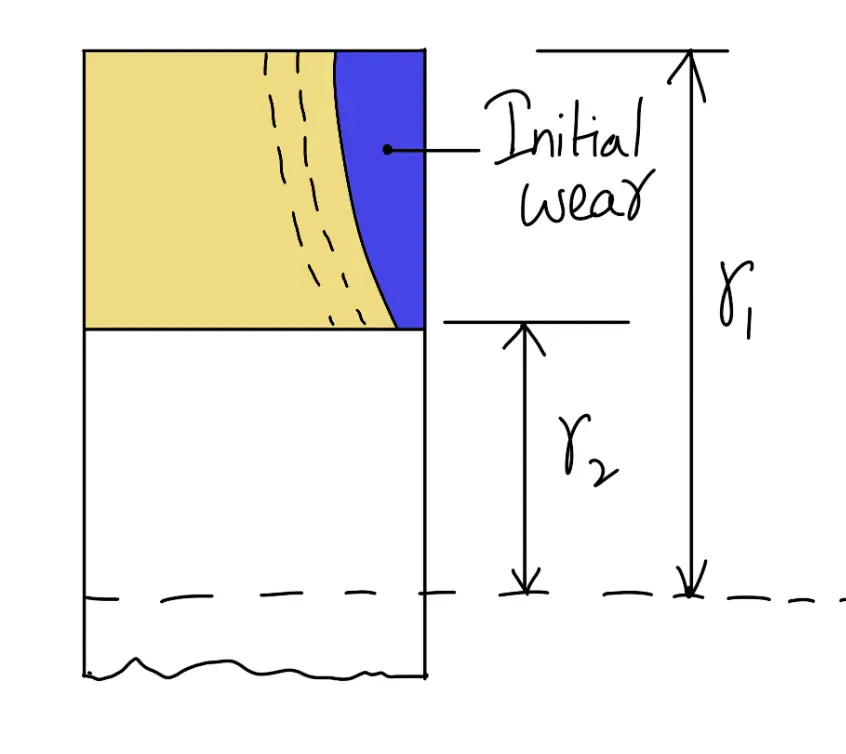
Let p be the normal intensity of pressure at a distance r from the axis of the clutch. Since the intensity of pressure varies inversely with the distance, therefore
p.r = C (a constant) or p=C/r
and the normal force on the ring,
δW = p.2πr.dr = (C/r) × 2πr.dr = 2πC.dr
∴ The total force acting on the friction surface,
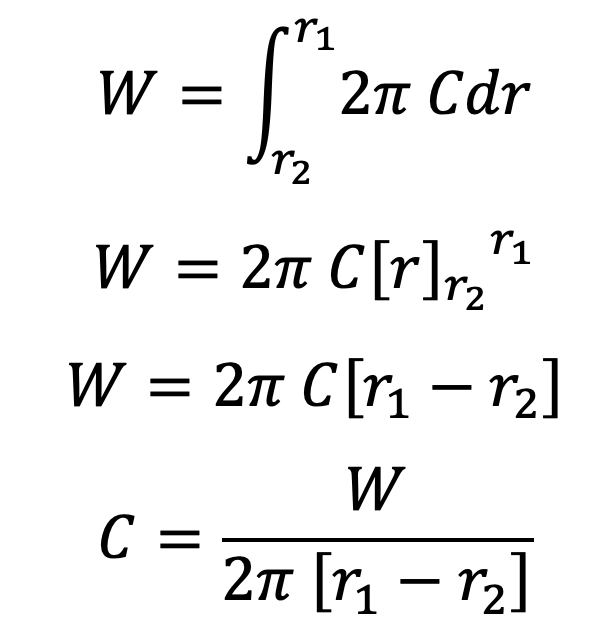
We know that the frictional torque acting on the ring,
T = 2πμ.p.r2.dr = 2πμ × (C/r) × r2.dr = 2πμ.C.r.dr
∴ Total frictional torque acting on the friction surface (or on the clutch),
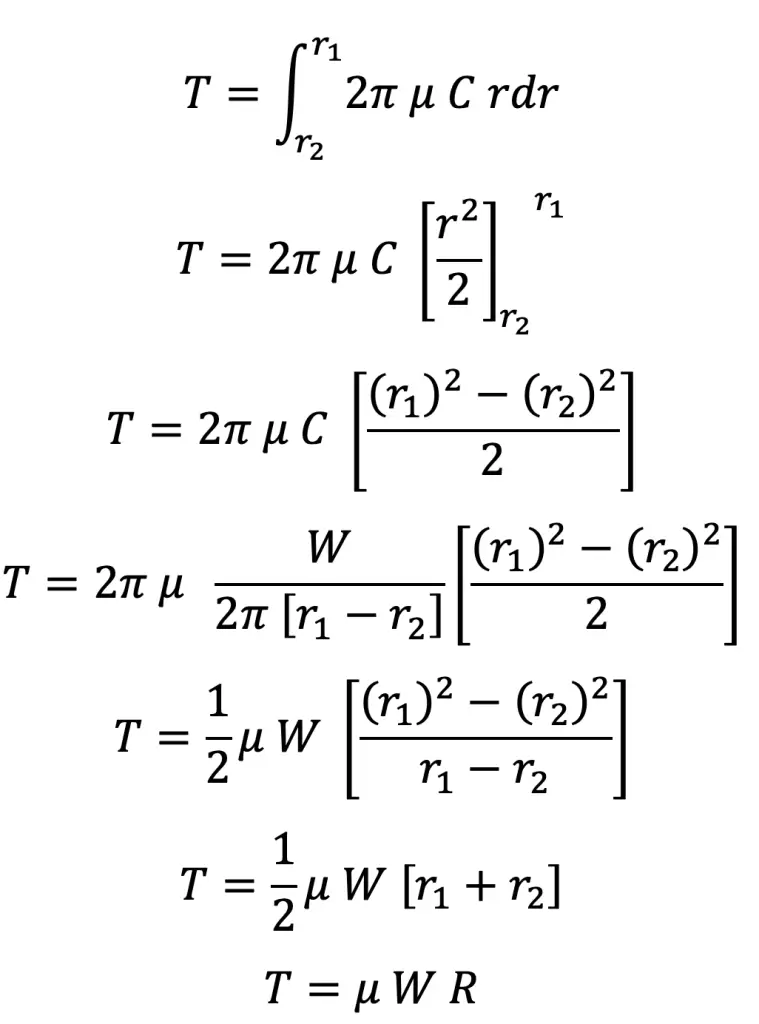
where R = (r1 + r2) / 2 = Mean radius of the friction surface.
👉Important points:
- In general, total frictional torque acting on the friction surfaces (or on the clutch) is given by
T = n.μ.W.R
Where
n = number of pairs of friction (or contact) surfaces
R = Mean radius of friction surface
For uniform pressure
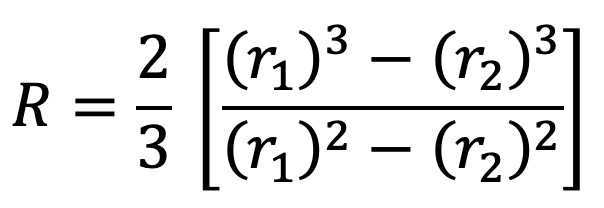
For uniform wear
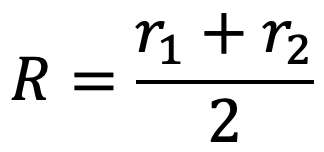
- For a single disc or plate clutch, normally both sides of the disc are effective. Therefore a single disc clutch has two pairs of surfaces in contact (i.e. n = 2).
- Since the intensity of pressure is maximum at the inner radius (r2) of the friction or contact surface, therefore equation may be written as
pmax × r2 = C or pmax = C/r2
- Since the intensity of pressure is minimum at the outer radius (r1) of the friction or contact surface, therefore equation may be written as
pmin × r1 = C or pmin = C/r1
- The average pressure ( pav) on the friction or contact surface is given by
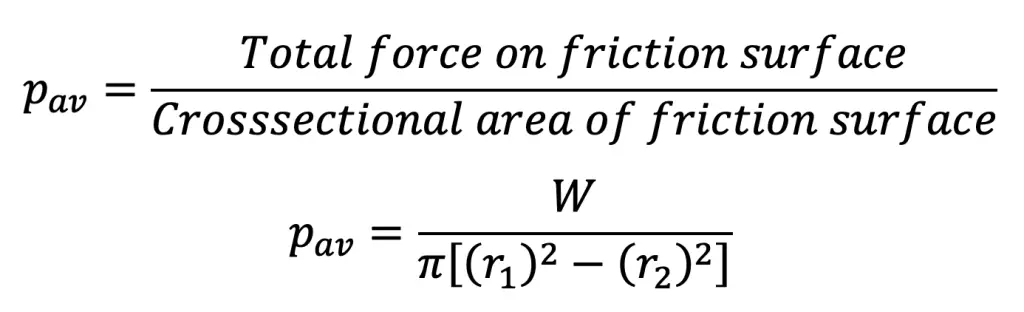
- In the case of a new clutch, the intensity of pressure is approximately uniform, but in an old clutch, the uniform wear theory is more approximate.
- The uniform pressure theory gives a higher friction torque than the uniform wear theory. Therefore in case of friction clutches, uniform wear should be considered, unless otherwise stated.
Multiple Disc Clutch
A multiple-disc clutch, as shown in the following figure, may be used when a large torque is to be transmitted. The inside discs (usually of steel) are fastened to the driven shaft to permit axial motion (except for the last disc).
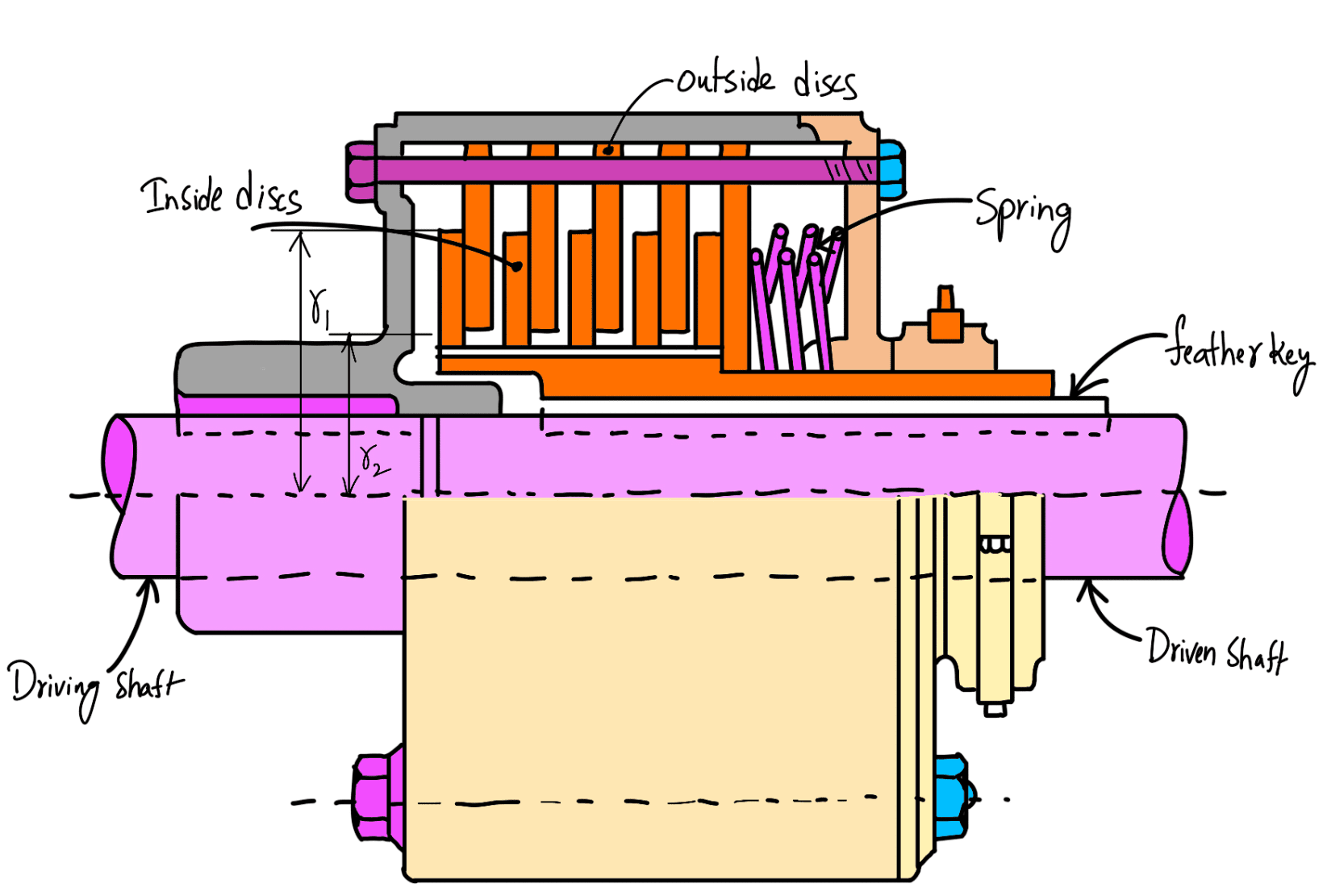
The outside discs (usually of bronze) are held by bolts and are fastened to the housing which is keyed to the driving shaft. The multiple disc clutches are extensively used in motor cars, machine tools, etc.
Let
n1 = Number of discs on the driving shaft
n2 = Number of discs on the driven shaft
Number of pairs of contact surfaces,
n = n1 + n2 – 1
and total frictional torque acting on the friction surfaces or on the clutch,
T = n.μ.W.R
Where
R = Mean radius of friction surfaces
For uniform pressure
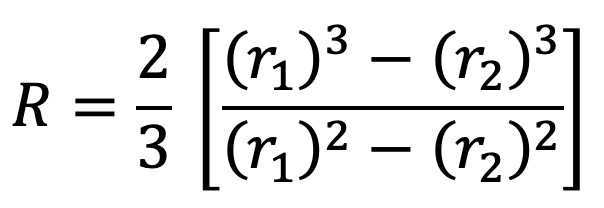
For Uniform Wear
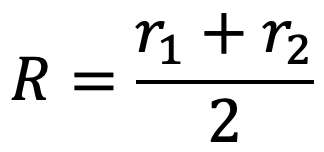
Design of a Disc Clutch with an example
Let us solve an Example Problem to understand the Design of a Disc Clutch or a plate clutch.
Problem Statement: A dry single plate clutch is to be designed for an automotive vehicle whose engine is rated to give 100 kW at 2400 r.p.m. and a maximum torque of 500 N-m. The outer radius of the friction plate is 25% more than the inner radius. The intensity of pressure between the plate is not to exceed 0.07 N/mm2. The coefficient of friction may be assumed equal to 0.3. The helical springs required by this clutch provide the axial force necessary to engage the clutch eight. If each spring has a stiffness equal to 40 N/mm, determine the dimensions of the friction plate and initial compression in the springs.
Answer:
Given Data
Power P = 100 kW = 100×103 W
Speed N = 2400r.p.m.
Torque T = 500N-m = 500×103 N-mm
Intensity of pressure p = 0.07N/mm2
coefficient of friction μ = 0.3
No. of springs = 8
Stiffness/spring = 40 N/mm
Dimensions of the friction plate
Let
r1 = Outer radius of the friction plate
r2 = Inner radius of the friction plate
Since the outer radius of the friction plate is 25% more than the inner radius, therefore
r1 = 1.25r2
For uniform wear conditions, p.r = C (a constant). Since the intensity of pressure is maximum at the inner radius (r2), therefore
p.r2 = C or C=0.07r2 N/mm
and axial load acting on the friction plate,
W = 2πC (r1 –r2) = 2π × 0.07 r2 (1.25r2 –r2) = 0.11(r2)2 N
We know that the mean radius of the friction plate, for uniform wear,
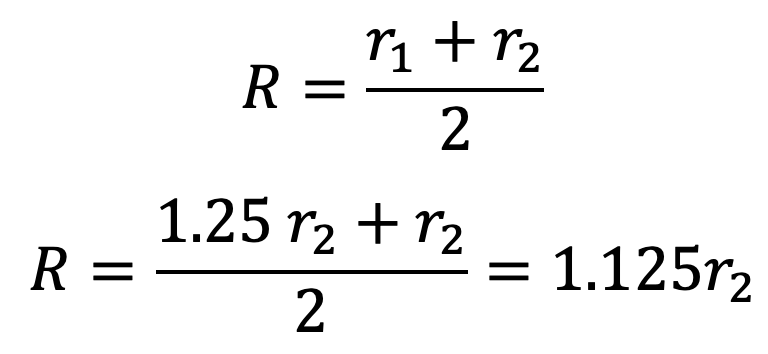
From the Torque transmitted (T ),
T = n.μ.W.R
500 × 103 = 2 × 0.3 × 0.11 (r2)2 × 1.125 r2
500 × 103 = 0.074 (r2)3
(r2)3 = 500 × 103 ÷ 0.074
r2 = 190 mm
We also know,
r1 = 1.25 r2
r1 = 1.25 × 190
r1 = 237.5 mm
With help of these parameters the Design of a Disc Clutch can be done.
Initial compression in the springs
We know that the total stiffness of the springs,
s = Stiffness per spring × No. of springs
s = 40 × 8
s = 320 N/mm
The axial force required to engage the clutch,
W = 0.11 (r2)2 = 0.11 (190)2 = 3970 N
Initial compression in the springs = W/s = 3970/320 = 12.4mm
This is all about the Design of a Disc Clutch or Plate Clutch. Let us know what you think about this article in the comment section below.

Leave a Reply