A brake is a device by means of which artificial frictional resistance is applied to a moving machine member, in order to retard or stop the motion of a machine. In the process of performing this function, the brake absorbs either the kinetic energy of the moving member or potential energy given up by objects being lowered by hoists, elevators, etc. In the previous articles, we discussed how we can calculate the energy absorbed by a brake and Heat Dissipation during Braking. We have discussed the theory behind the Design of Differential Band Brakes in the previous article. In this article, let us use an example problem statement to understand the Design of a Differential Band Brake.

As we mentioned above that the brake is used to retard or stop the motion of a machine. This action is called Braking. In the process of braking, the brake absorbs either the kinetic energy of the moving member or potential energy given up by objects being lowered by hoists, elevators, etc. The energy absorbed by brakes is dissipated in the form of heat. This heat is dissipated in the surrounding air (or water which is circulated through the passages in the brake drum) so that excessive heating of the brake lining does not take place.
The design or capacity of a brake depends upon the following factors:
- The unit pressure between the braking surfaces
- The coefficient of friction between the braking surfaces
- The peripheral velocity of the brake drum
- The projected area of the friction surfaces
- The ability of the brake to dissipate heat is equivalent to the energy being absorbed.
The major functional difference between a clutch and a brake is that a clutch is used to keep the driving and driven member moving together, whereas brakes are used to stop a moving member or to control its speed.
We also solved an example problem to stop A vehicle of mass 1200 kg moving down the hill at a slope of 1:5. by finding how much amount of Braking Torque is required to stop the vehicle in the previous article.
Differential Band Brake
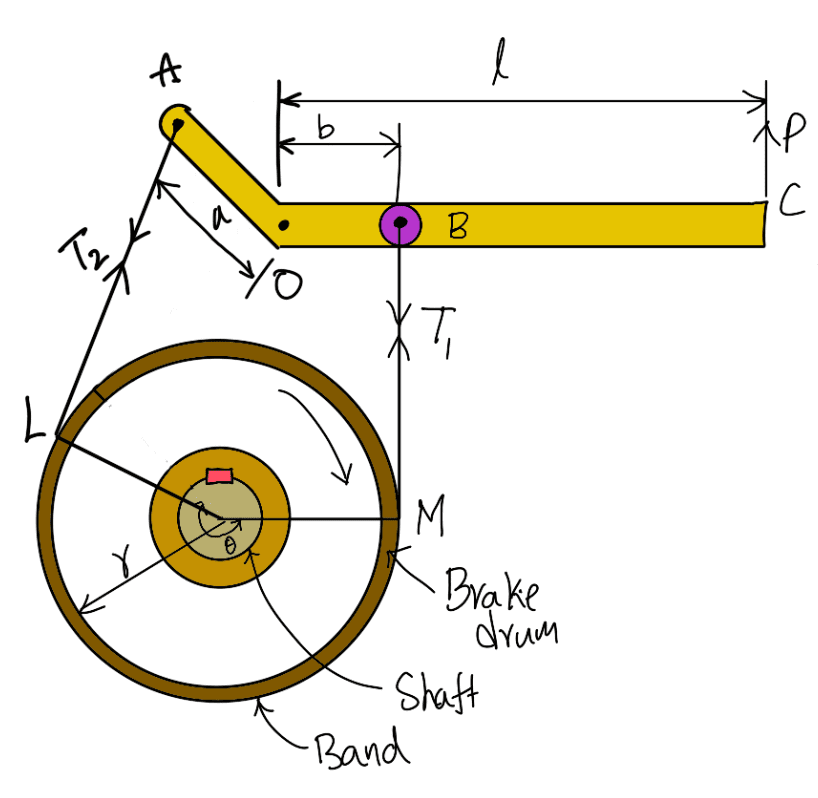
A band brake consists of a flexible band of leather, one or more ropes, or steel lined with friction material, which embraces a part of the circumference of the drum. A simple band brake in which one end of the band is attached to a fixed pin or fulcrum of the lever while the other end is attached to the lever at a distance b from the fulcrum. In a differential band brake, as shown in the following figure, the ends of the band are joined at A and B to a lever AOC pivoted on a fixed pin or fulcrum O. It may be noted that for the band to tighten, the length OA must be greater than the length OB.
As we mentioned above we have discussed the theory of Differential Band Brake in the previous article.
Example Problem on Design of a Differential Band Brake
Problem Statement: A differential band brake is operated by a lever of length 500 mm. The brake drum has a diameter of 500 mm and the maximum torque on the drum is 1000 N-m. The band brake embraces 2/3rd of the circumference. One end of the band is attached to a pin 100 mm from the fulcrum and the other end to another pin 80 mm from the fulcrum and on the other side of it when the operating force is also acting. If the band brake is lined with asbestos fabric having a coefficient of friction of 0.3, find the operating force required.
Design the steel band, shaft, key, lever, and fulcrum pin. The permissible stresses may be taken as 70 MPa in tension, 50 MPa in shear, and 20 MPa in bearing. The bearing pressure for the brake lining should not exceed 0.2 N/mm2.
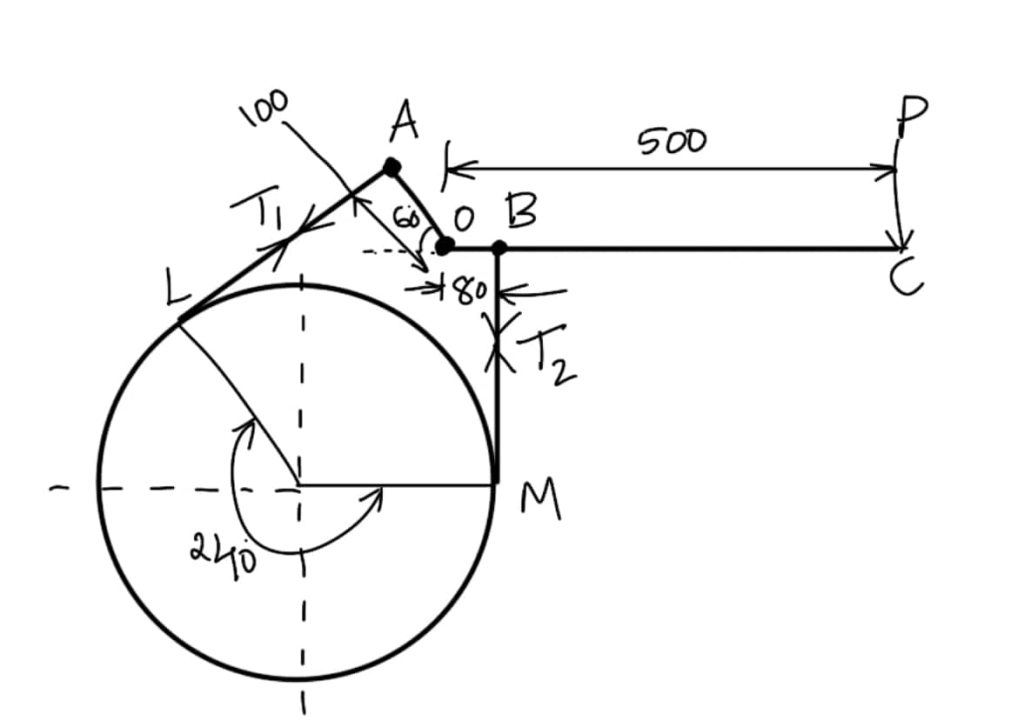
(All dimensions are in mm)
Answer (Design of a Differential Band Brake):
Given Data
Length of lever l = 500mm
Diameter of the brake drum d = 500mm or r = 250mm
Torque on the Drum TB = 1000N-m = 1×106 N-mm
Pin OA = 100mm
Pin OB = 80mm
Coefficient of friction μ = 0.3
Permissible tensile stresses σt = 70MPa = 70N/mm2
Permissible shear stressesτ = 50MPa = 50N/mm2
Permissible bearing stresses σb = 20MPa = 20N/mm2
Permissible bearing pressure pb = 0.2N/mm2
Operating Force
Let P = Operating force
The differential band brake is shown in the above figure Since OA > OB, therefore the operating force (P) will act downward. When the drum rotates anticlockwise, the end of the band attached to A will be tight with tension T1 and the end of the band attached to B will be slack with tension T2. First of all, let us find the values of tensions T1 and T2.
We know that the angle of the wrap,
θ = 2/3 rd of circumference
θ = (2/3) × 360∘
θ = 240 × (π/180)
θ = 4.19 rad.
and
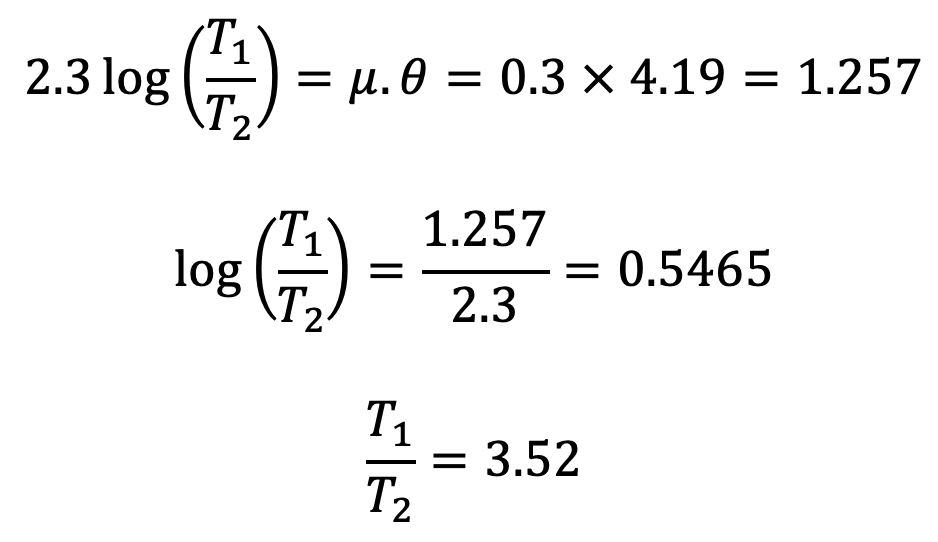
We know that the braking torque (TB),
1 × 106 = (T1 –T2)r
1 × 106 = (T1 –T2) 250
T1 –T2 = 1×106/250
∴ T1 –T2 = 4000N
From the above two equations, we have
T1 = 5587N
T2 = 1587N
Now taking moments about the fulcrum O, we have
P × 500 = T1 × 100 – T2 × 80
P × 500 = 5587 × 100 – 1587 × 80
P × 500 = 431740
P = 431740/500
∴ P = 863.5N
The Operating force P is 863.5N.
Design for steel band
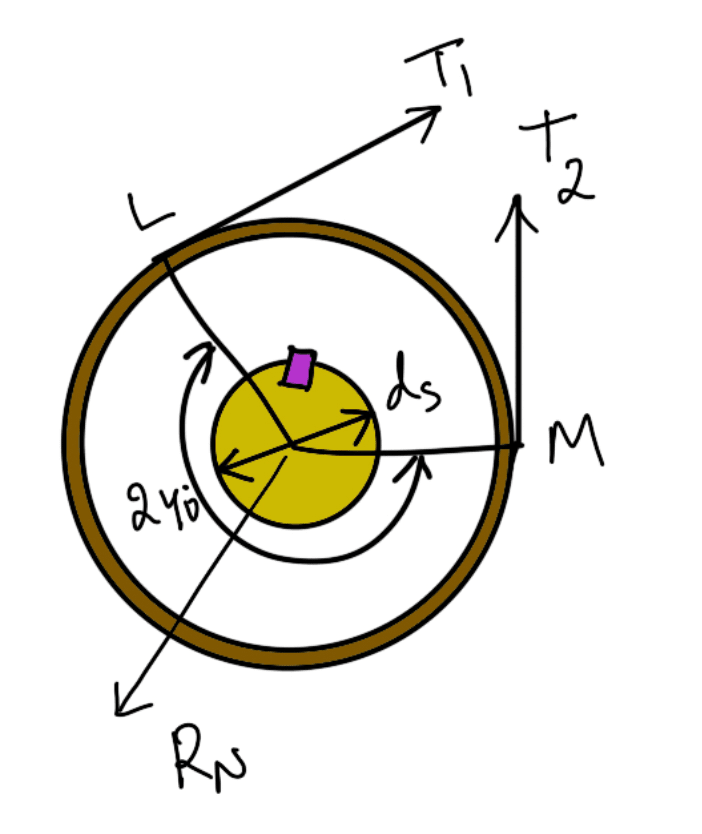
Let
t = Thickness of band in mm
b = Width of the band in mm
We know that the length of contact of the band, as shown in the above figure,

∴ Area of contact of the band,
Ab = Length × Width of band = 1047 b mm2
We know that normal force acting on the band,
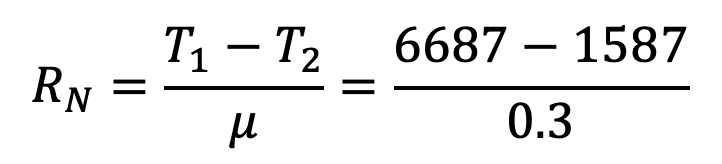
RN = 133333N
We also know that normal force on the band (RN),
13333 = pb × Ab
13333 = 0.2 × 1047b
13333 = 209.4b
b = 13 333/209.4
∴ b = 63.7
Let us take the Width of the band (b) as 64mm.
and cross-sectional area of the band,
A = b × t = 64t mm2
∴ The tensile strength of the band = A × σt = 64t × 70 = 4480t N
Since the band has to withstand a maximum tension (T1) equal to 5587 N, therefore
4480t = 5587
t = 5587/4480
t = 1.25mm
The thickness of the band (t) is 1.25mm.
Design of shaft
Let
ds = Diameter of the shaft in mm.
Since the shaft has to transmit torque equal to the braking torque (TB), therefore
1 × 106 = (π/16) × τ (ds)3
1 × 106 = (π/16) × 50 (ds)3
1 × 106 = 9.82 (ds)3
(ds)3 = 1 × 106/9.82
(ds)3 = 101833
ds = 46.7
Let us say the Diameter of the shaft is 50mm.
Design of key
The standard dimensions of the key for a 50 mm diameter shaft are as follows:
Width of key w = 16 mm
The thickness of key, t1 = 10 mm
Let l = Length of the key
Considering the shearing of the key, we have braking torque (TB),
1 × 106 = l × w × τ × (ds/2)
1 × 106 = l × 16 × 50 × (50/2)
1 × 106 = 20 × 103 l
l = (1 × 106) ÷ (20 × 103)
l = 50mm
The Length of the key is 50mm.
We can also determine the dimensions of the key from the following relations :
w = (ds/4) + 3 mm
t1 = w/2
Design for lever
Let
t2 = Thickness of lever in mm
B = Width of the lever in mm
It is assumed that the lever extends up to the center of the fulcrum. This assumption results in a slightly stronger lever. Neglecting the effect of T2 on the lever, the maximum bending moment at the center of the fulcrum.
M = P × l
M = 863.5 × 500
M = 431750 N-mm
and section modulus,
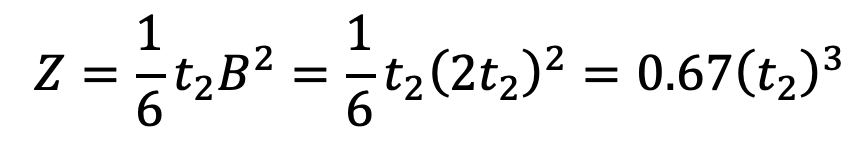
We know that bending tensile stress (σt),
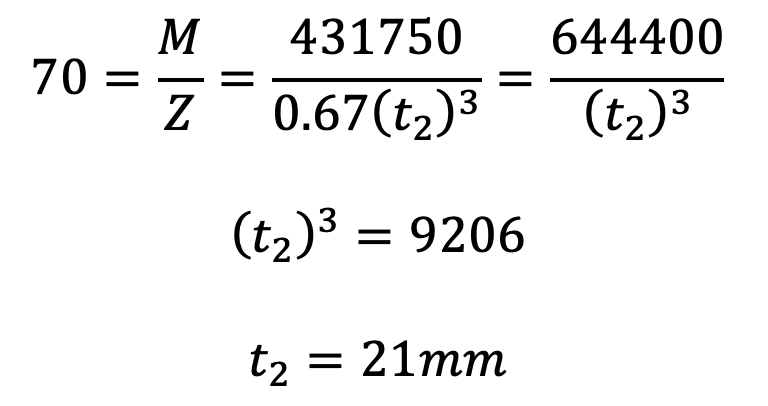
The Thickness of the lever (t2 ) is 21mm.
The Width of the lever is B = 2 t2 =2 × 21 = 42mm.
Design for fulcrum pin
Let
d1 = Diameter of the fulcrum pin
l1 = Length of the fulcrum pin.
First of all, let us find the resultant force acting on the pin. Resolving the three forces T1, T2, and P into their vertical and horizontal components, as shown in the following figure.
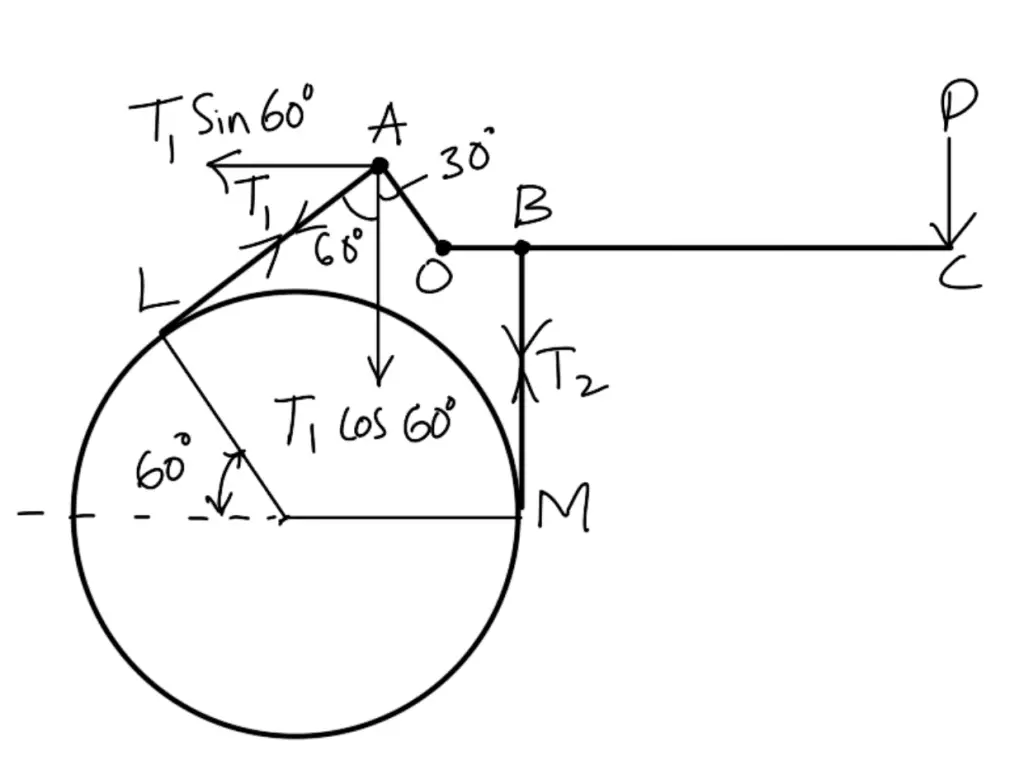
We know that the sum of vertical components,
Σ V = T1 cos 60° + T2 + P
Σ V = 5587 × 0.5 + 1587 + 863.5
Σ V = 5244 N
and the sum of horizontal components,
ΣH = T1 sin60° = 5587 × 0.866 = 4838N
∴ The resultant force acting on the pin,
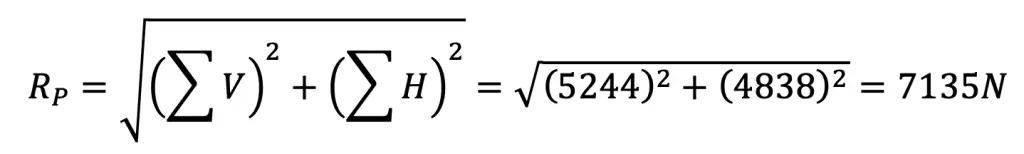
Considering the bearing of the pin, we have the resultant force on the pin (RP),
7135 = d1.l1.σb
7135 = d1 × 1.25 d1 × 20
7135 = 25 (d1)2
(d1)2 = 7135/25
(d1)2 = 285.4
d1 = 16.9
Let us say the Diameter of the fulcrum pin (d1) is 18mm.
The Length of the fulcrum pin l1 is = 1.25 d1 = 1.25 × 22.5 mm
Let us now check the pin for induced shear stress. Since the pin is in double shear, therefore resultant force on the pin (RP),
7135 = 2 × (π/4) (d1)2 τ
7135 = 2 × (π/4) (18)2 τ
7135 = 509 τ
τ = 7135 ÷ 509
τ = 14 N/mm2
This induced shear stress is within permissible limits.
The pin may be checked for induced bending stress. We know that the maximum bending moment,
M = (5/24) × W l1 = (5/24) × 7135 × 22.5
M = 33 445 N-mm
and section modulus,
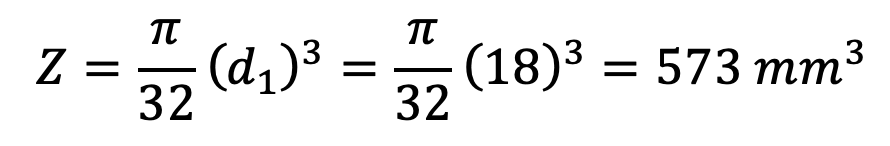
∴ Bending stress induced
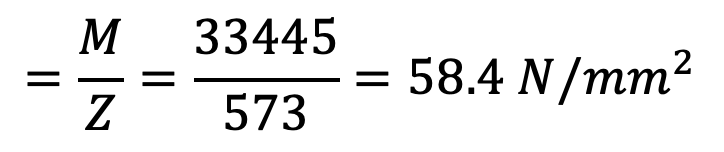
This induced bending stress in the pin is within the safe limit of 70 N/mm2.
The lever has an eye hole for the pin and connectors at the band have a forked end. A brass bush of 3 mm thickness may be provided in the eye of the lever. Therefore, the diameter of the hole in the lever
= d1 + 2 × 3 = 18 + 6 = 24mm
The boss is made at the pin joints whose outer diameter is equal to twice the diameter of the pin and length equal to the length of the pin. The inner diameter of the boss is equal to the diameter of the hole in the lever.
∴ The outer diameter of the boss = 2d1 = 2 × 18 = 36mm
and length of boss = 22.5 mm
Let us now check the induced bending stress in the lever at the fulcrum. The section of the lever at the fulcrum is shown in the following figure.
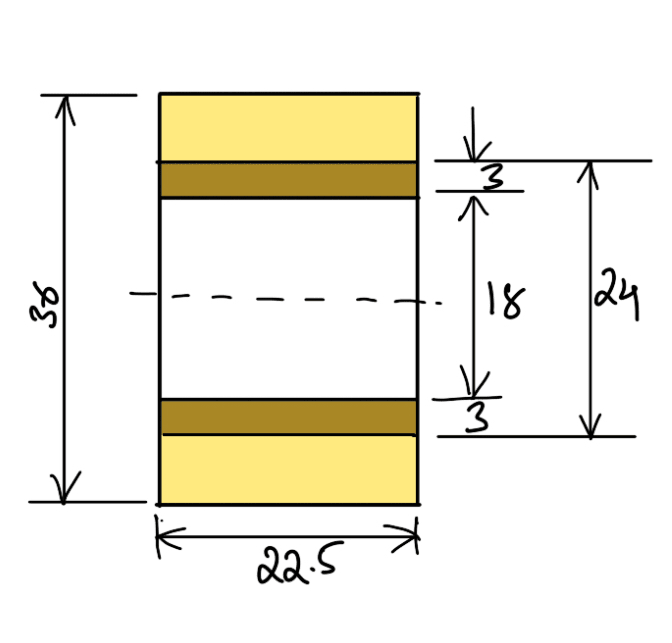
We know that the maximum bending moment at the fulcrum,
M = P × l = 863.5 × 500 = 431750N-mm
and section modulus,
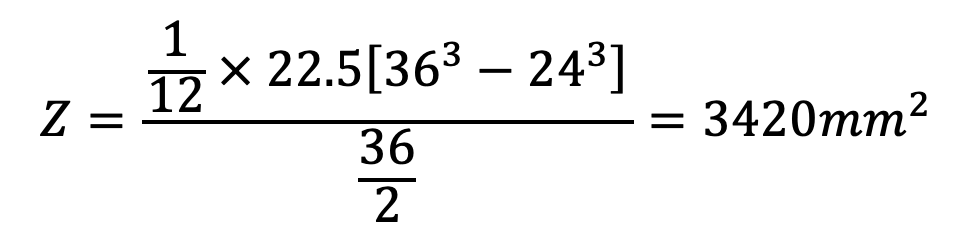
∴ Bending stress induced in the lever
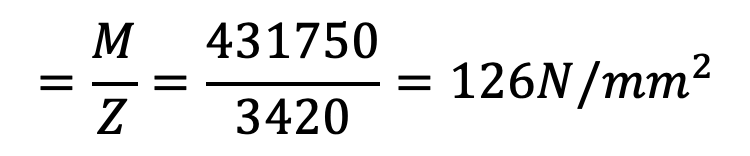
Since the induced bending stress is more than the permissible value of 70 N/mm2, therefore the diameter of the pin is required to be increased. Let us take
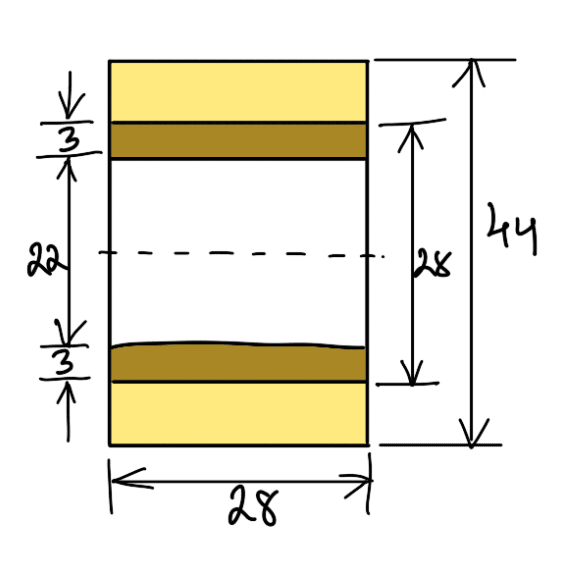
Diameter of pin, d1 = 22 mm
∴ Length of the pin, l1 = 1.25 d1 = 1.25 × 22 = 27.5 Let us take 28mm as the length of the pin.
Diameter of hole in the lever = d1 + 2 × 3 = 22 + 6 = 28mm
The outer diameter of the boss = 2d1 = 2 × 22 = 44mm = Outer diameter of eye
The thickness of each eye = l1/2 = 28/2 = 14mm
A clearance of 1.5 mm is provided on either side of the lever in the fork.
The new section of the lever at the fulcrum will be shown in the following figure.
Section modulus,
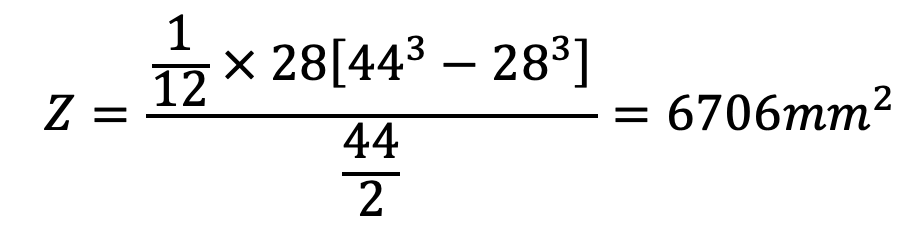
and induced bending stress
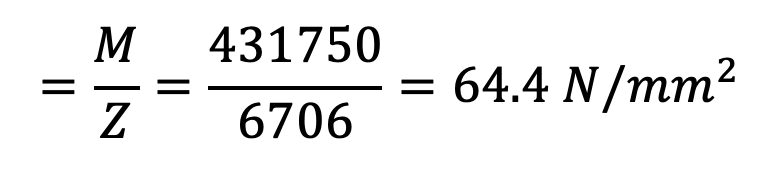
This induced bending stress is within permissible limits.
This is all about the Design of a Differential Band Brake. Let us know what you think about this article in the comment section below.

Leave a Reply