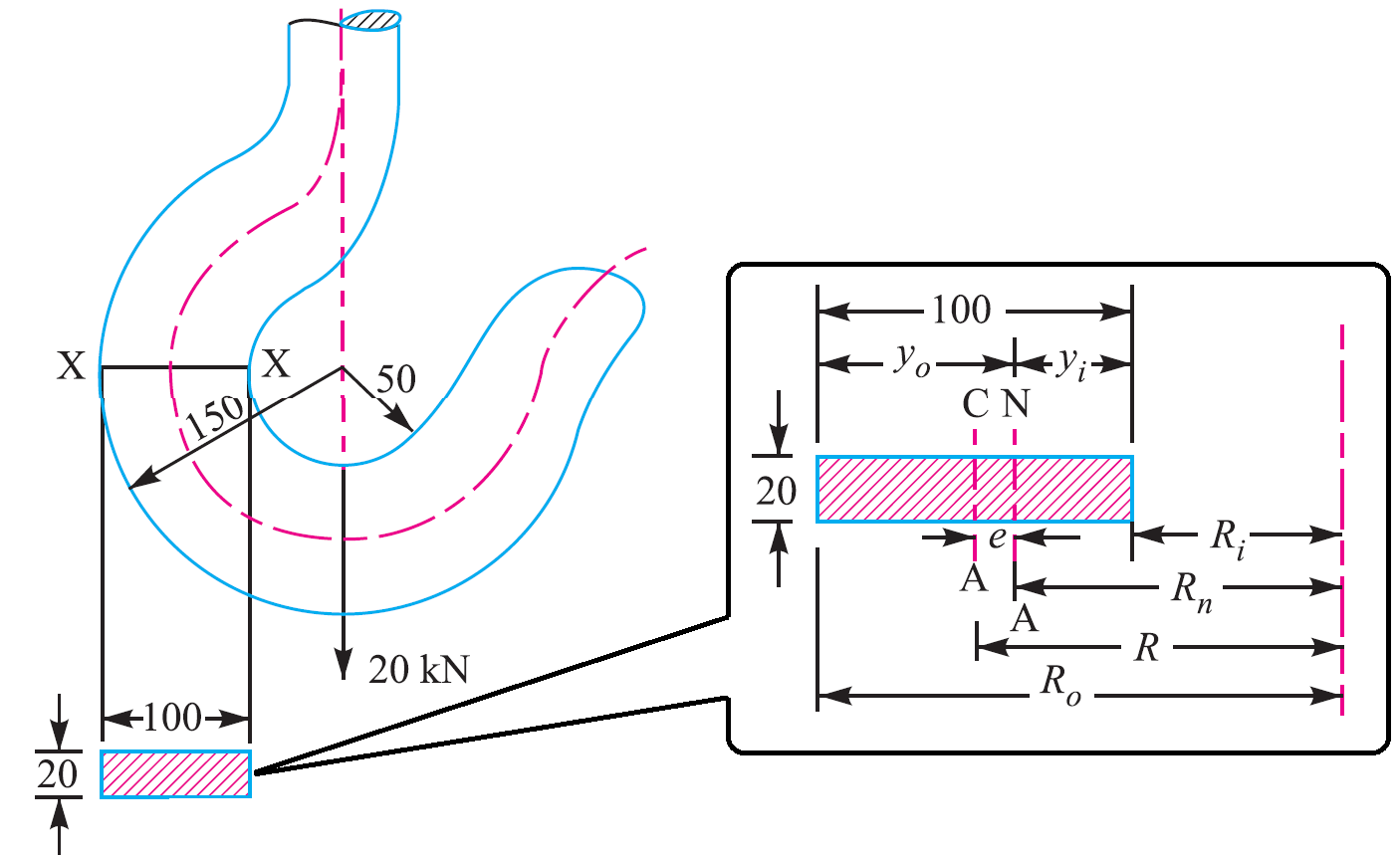
Crane Hook Design Problem: The crane hook carries a load of 20 kN as shown in given below Fig. The section at X-X is rectangular whose horizontal side is 100 mm. Find the stresses in the inner and outer fibres, the given section.
Solution:
Given data (All are in Metric Units)
Load (W) = 20kN = 20 x 10³N
The radius of curvature of the inside fibre (Ri) = 50 mm
The radius of curvature of the outside fibre (Ro) = 150 mm
The radius of curvature of the neutral axis (Rn) =?
The radius of curvature of the Centroidal axis (R) =?
The distance between neutral axis to the inside fibre (Yi ) = Rn-Ri
The distance between neutral axis to the outside fibre (Yo) = Ro – Rn
Section X-X height (h) = 100 mm
Section X-X breadth (b) = 20 mm
Area of this rectangular section X-X (A)= Breadth(b) x Height(h) = 20×100 = 2000 mm²
[Read about: Bending stress in curved Beams]
This Crane hook is considered as the initially curved beam. So We have to find the radius of curvature for both neutral axis and centroidal axis. Following are the standard formulas for the radius of curvature of the neutral axis (Rn) and Centroidal axis (R) respectively,
From the above equations (Calculated values)
The radius of curvature of the neutral axis (Rn) = 91.07 mm
The radius of curvature of the Centroidal axis (R) = 100mm
The distance between the Centroidal axis and Neutral axis (e) = R-Rn = 100-91.07 = 8.93 mm
The distance between the centroidal axis to the load acting (x) = R = 100 mm
The distance between neutral axis to the inside fibre (Yi ) = Rn-Ri = 91.07-50 = 41.07mm
The distance between neutral axis to the outside fibre (Yo) = Ro – Rn = 150-91.07 = 58.93 mm
Finding Bending Moment
Bending moment about the centroidal axis is (M) = Load x distance between the load acting and the section (∴ Here, in this case, it is R)
M = W x x = 20 x 10³ x 100 = 2 x 106 N-mm
The bending moment is (M) = 2 x 106 N-mm at the section X-X
Finding Tensile Stress
Here the section is applicable to the tensile load of 20 x 10³N. We have to find the tensile load at this section X-X
σt = Load /Area
σt = 20 x 10³ /2000 = 10 N/mm² = 10MPa
Finding Maximum Bending Stress at the Inside Fibre
The maximum Bending stress at inside fibre is given by
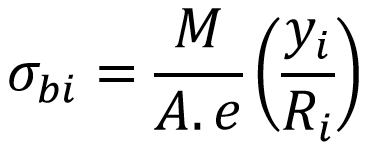
By substitutions
= 92 N/mm² (92 MPa)
Finding Maximum Bending Stress at the Outside Fibre
The maximum Bending stress at outside fibre is given by
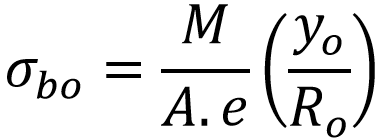
By substitutions
= 44 N/mm² (44MPa)
Finding Resultant Stress at Inside Fibre
The resultant stresses at the Inside Fibre = σt+σbi
= 10+92 = 102 N/mm² (102 MPa)
The resultant stresses at the Inside Fibre are 102 MPa and it is a tensile stress.
Finding Resultant Stress at Outside Fibre
The resultant stresses at the Outside Fibre = σt-σbo
= 10-44 = -34 N/mm² (-34 MPa)
The resultant stresses at the Outside Fibre are 34 MPa and it is a Compressive Stress.
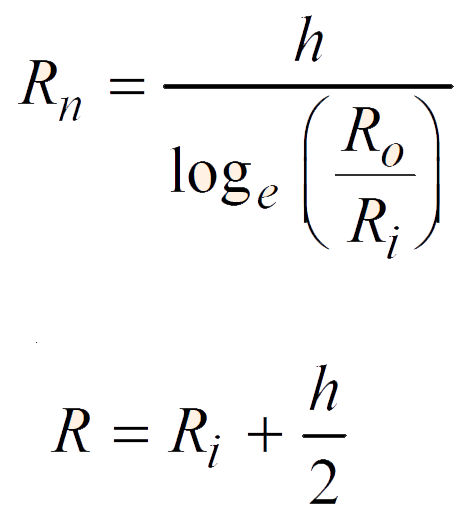

Leave a Reply