What is the Brayton cycle?

As we have already discussed the Diesel Cycle, This Brayton Cycle is the extension for the Diesel Cycle and the Gas turbines work based on this Brayton Cycle. Let’s discuss this in detail.

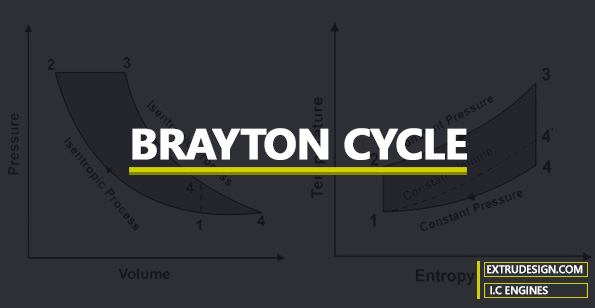
Brayton cycle

The Brayton Cycle is the Theoretical Cycle for the Gas Turbine.

This cycle is a modification to the Diesel Cycle. In Diesel Cycle there are two Isentropic processes and the third one is a Constant volume and the fourth one is a constant Pressure process.

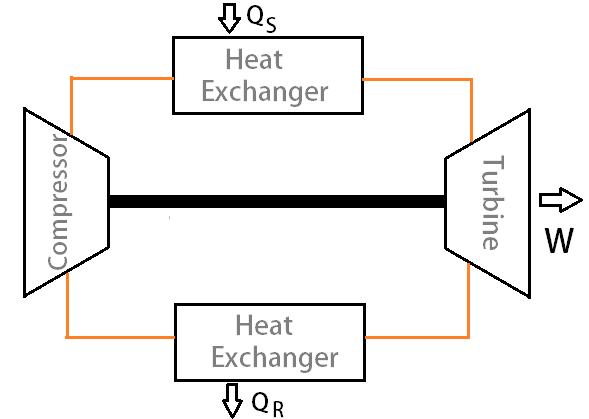
Actually, there are two types of Brayton Cycles. They are Open Brayton Cycle and the Closed Brayton Cycle.

• The Open Brayton Cycle is the representation for the Internal Combustion Engine, where the working fluid will not be reused and it will be exhausted to the atmosphere. This principle is used in the jet propulsion. This open Gas turbine cycle is the Ideal for the Brayton cycle.
• Whereas the closed Brayton cycle represents the Gas Turbine where the working fluid will be reused. This principle is used in the Electric power generations.

Check the P-V diagram and the T-S Diagram for both the Ideal Brayton Cycle and the Diesel Cycle.

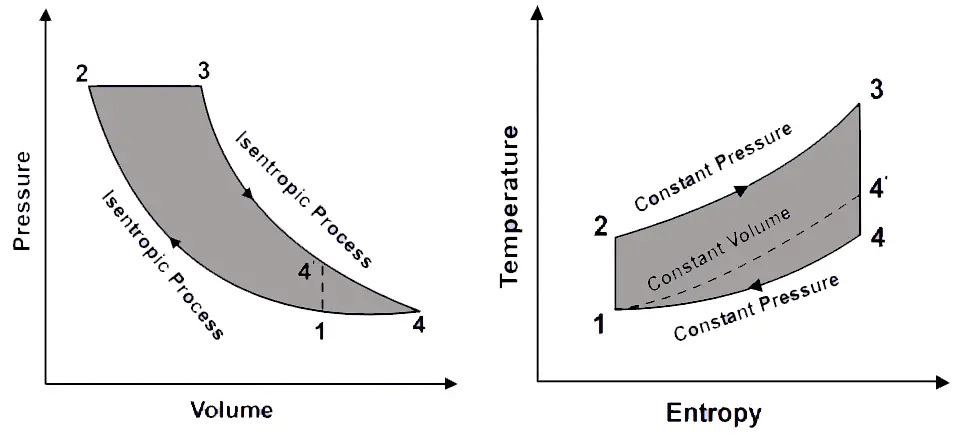
From the above graphs, we can observe that the Isentropic expansion of the Diesel Cycle is further extended in the Brayton Cycle to increase the cycle efficiency.

Let’s see how all the four processes will work in the open Gas Turbine (Ideal Brayton Cycle).

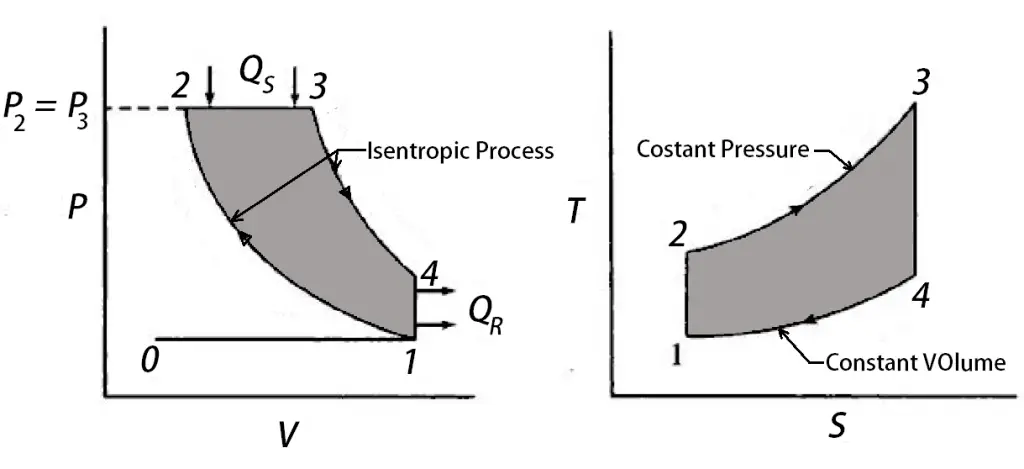
1 → 2

This 1 → 2 is the Isentropic Compression process. In this process, the compressor in the gas turbine takes in fresh ambient air, compresses it to a higher temperature and pressure.

2 → 3

2 → 3 is the constant Pressure Heat addition. In this process, the Fuel and the higher pressure air from the compressor are sent to a combustion chamber, where fuel is burned at constant pressure. The resulting high-temperature gases sent to the turbine.

3 → 4

3 → 4 is the Isentropic Expansion process. The high-temperature gases expand to the ambient pressure in the turbine and produce power. This expansion process will be continued until the combustion gasses expand until its lowest pressure to get the maximum efficiency.

4 → 1

4 → 1 is the Constant pressure heat rejection processes. In this process, the exhaust gases leave the turbine.

How the efficiency will be Increase by extending the Expansion stroke for the lowest pressure?

During the Expansion process and the exhaust process 3 → 4 & 4 → 1 respectively, the indicated power generated supposed to be completely utilised, but it is not happening in the Diesel cycle. So If we extend the expansion stroke till the combustion particles to expand till its lowest pressure, then we can utilise the entire indicated power generated in the cycle to increase the efficiency of the Brayton cycle.

Efficiency of the Ideal Brayton Cycle

Thermodynamically, the efficiency of the Diesel Cycle is given by

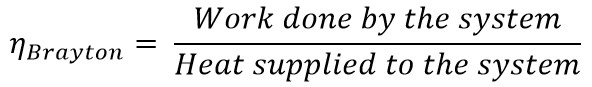
Work done by the system = Heat supplied (Q_S)- Heat rejected (Q_R)

W = Q_S – Q_R

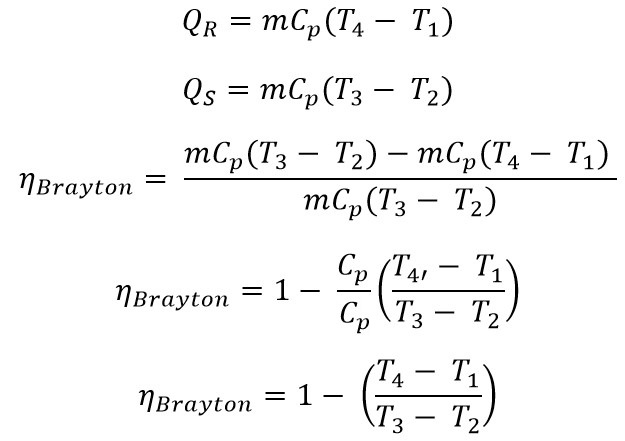
Note: r is the compression Ratio whereas the r_p is the pressure ratio

Considering the 3 → 4 process

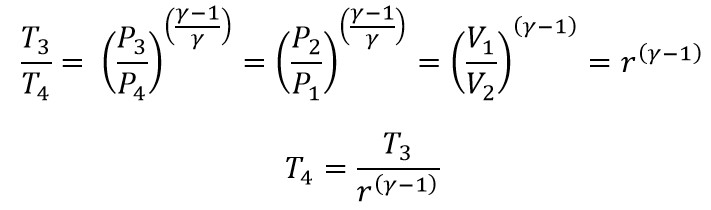
Similarly from the 1 → 2 process

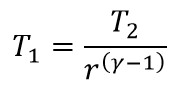
By substituting the T₁, T₄ in the above Efficiency formula

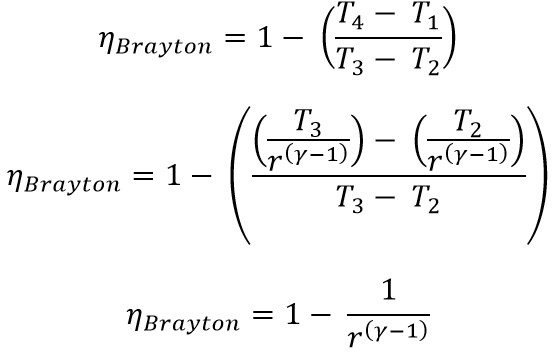
From the relation between the Compression ratio and the pressure ratio.

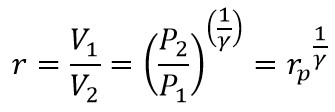
From the above equation, the efficiency equation can be written as

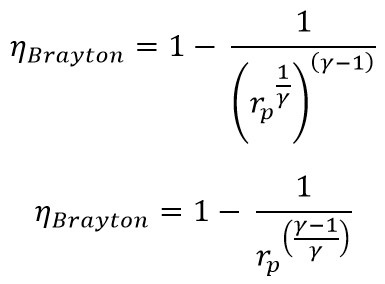
From the above equation, we can observe that the efficiency of the Brayton cycle depends on the pressure ratio and the specific heat of the working fluid.

In the Brayton cycle, the work output will depend on the initial temperature and the ratio of the maximum temperature to the minimum temperature, the pressure ratio and the specific heat.

Conclusion

We have discussed how the Brayton Cycle is extended to get the maximum efficiency from the engine and also we have derived the efficiency equation for the Brayton Cycle. Please let us know your thoughts in the comment section below.