When a machine component is subjected to a load (Static or dynamic load), it will experience the bending along its length due to the stress induced in it. This stress is known as Bending stress. Besides, there are other types of stress are also induced. they are Tensile stress, Compressive stress, Shearing stress, Bearing stress, Torsional stress. In this case, we supposed to consider the beam subjected to pure bending only.

Bending stress

Bending stress is the normal stress induced in the beams due to the applied static load or dynamic load. The study of bending stress in beams will be different for the straight beams and curved beams. In this article, we will discuss the Bending stress in the straight beams only.

Bending stress in straight beams

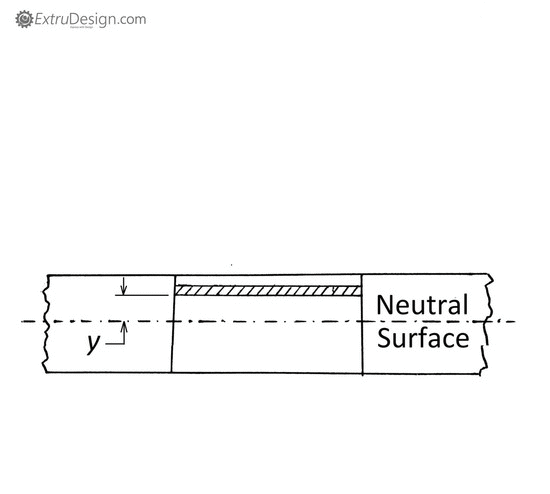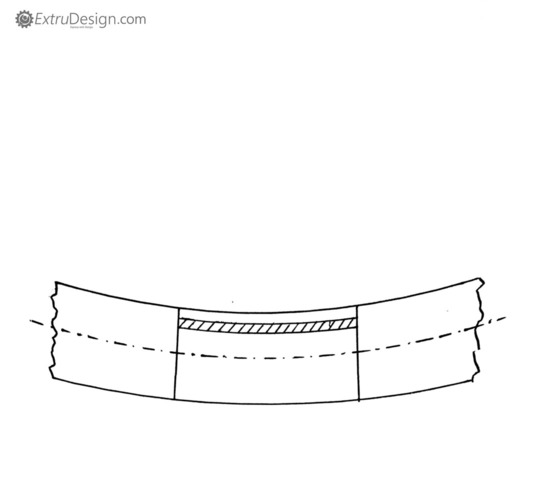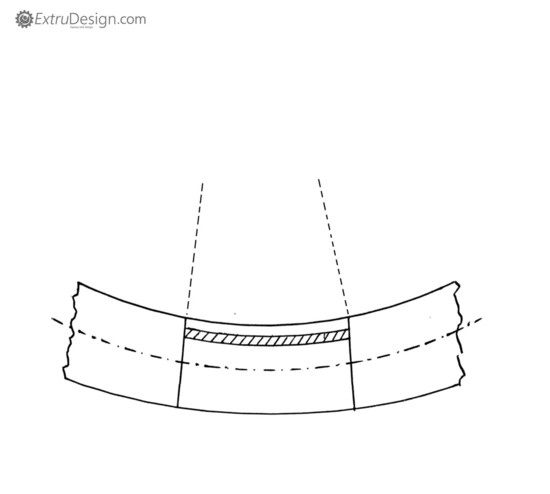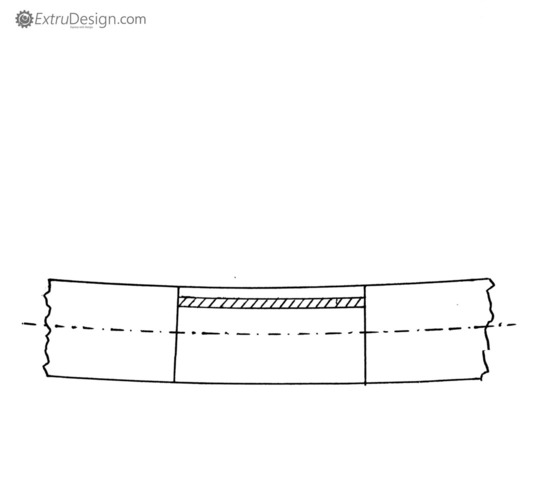
Consider a straight beam which is subjected to a bending moment M.

1. While bending in the beam, the fibres in the upper side in the beam tend to compress (shortened) whereas the fibres in the lower side tend to elongate.
2.  In between somewhere these upper fibres and the lower fibres, few fibres neither elongate nor shortened. This part of the surface is known as the neutral surface.
3. The intersection of these neutral surfaces with any normal cross-section of the beam is known as the Neutral Axis.

 

From the Bending Equation

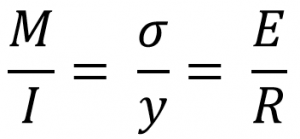
Where

M = Bending moment at the given section.

I = Moment of inertia of the cross-section about the neutral axis.

σ = Bending stress.

y = Distance between the neutral axis and the fibre(The hatched portion is the considered fibre to calculate the bending stress)

E = Young’s modulus of the material of the beam.

R = Radius of the curvature of the beam.

From the above bending equation, we can write

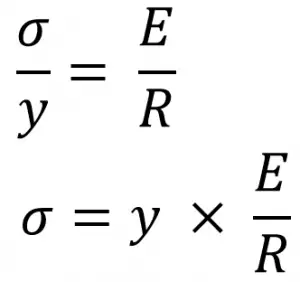
Here E and R are constants, therefore within the elastic limit, the stress is directly proportional to the distance between the neutral axis and the fibre (y).

σ ∝ y

From the above bending equation, we can also write

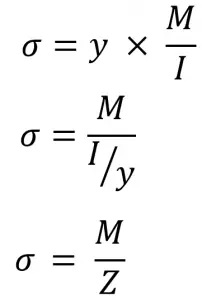
Where Z is the section modulus.

 

Considerations in the Bending Stress in the Straight Beams

There are some considerations has to made while finding the bending stress for the straight beams. They are as follows

• It has to consider that the material throughout the beam is same (Homogeneous material)
• It should obey the Hooke’s law (Stress is directly proportional to the strain in the beam)
• Each layer in the beam has to expand or contract freely and independently.
• The load should be applied in the plane of bending
• The Young’s modulus is to be same for both the tension and the compression.
• The neutral axis has considered to always pass thru the centroid of the beam.
• For the Symmetrical section(Circle, square, rectangle) the neutral axis passes thru the geometric centre

Conclusion

For symmetric section beams, it is a bit easy to find out the bending stress as we mentioned, if it is an unsymmetrical section then centroid of the beam has to find. then we need to find the distance of the extreme fibres for both lower and upper fibres.