Optical Interference is an effect that can occur when two or more light beams are superimposed. We knew that a ray of light is composed of an infinite number of waves of equal wavelength. the value of the wavelength determines the colour of light.

For the sake of simplicity, let us consider two waves, having a sinusoidal property, from two different light rays. The below figure illustrates the combined effect of the two waves of light. The two rays, A and B, are in phase at the origin O and will remain so as the rays propagate through a large distance.
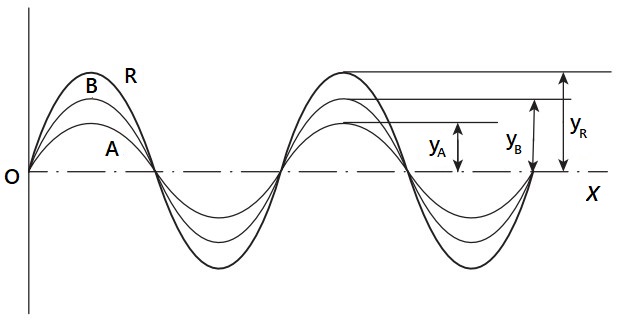
Suppose the two rays have amplitudes yA and yB,
then the resultant wave will have an amplitude yR = yA + yB
Thus, when the two rays are in phase, the resultant amplitude is maximum and the intensity of light is also maximum. However, if the two rays are out of phase, say by an amount d, then the resultant wave will have an amplitude will be
yR = (yA + yB) cos𝛿/2
It is clear that the combination of the two waves no longer produces maximum illumination.
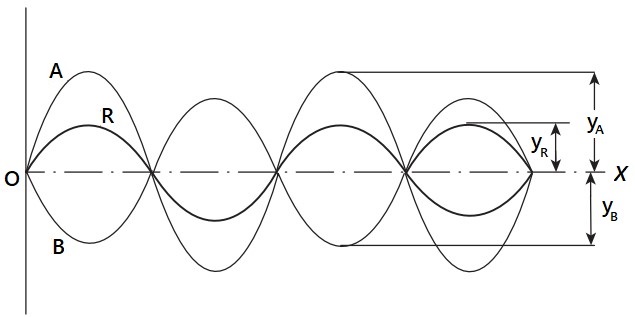
Consider the case where the phase difference between the two waves is 180°. The amplitude of the resulting wave, which is shown in the above figure, is the algebraic sum of yA and yB. The corollary is that if yA and yB are equal, then yR will be zero since cos(180/2) is zero. This means that complete interference between two waves having the same wavelength and amplitude produces darkness.
One of the properties of light is that light from a single source can be split into two component rays. Observing the way in which these components recombine shows us that the wavelength of light can be used for linear measurement. The linear displacement d between the wavelengths of the two light rays results in maximum interference when d = λ/2
Where λ is the wavelength of light.
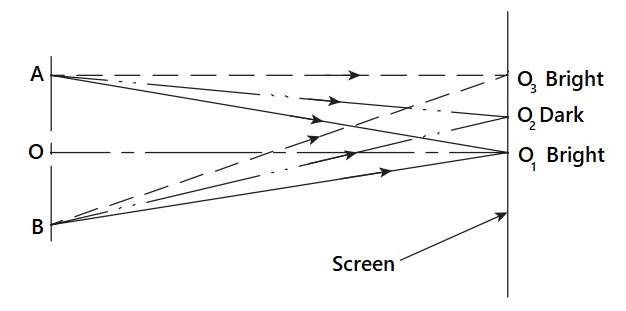
Now in what way is this property going to help us in taking linear measurements? The above Figure illustrates how the property of interference of light can be used for linear measurement. Let us consider two monochromatic light rays from two-point sources, A and B, which have the same origin. The light rays are made to fall on a flat screen that is placed perpendicular to the axis OO1. The axis OO1 is in turn perpendicular to the line joining the two-point sources, A and B. Since both rays originate from the same light source, they are of the same wavelength. Let us also assume that the distances OA and OB are equal.
Now, consider the convergence of two rays at point O1 on the screen. Since the distances AO1 and BO1 are equal, the two rays are in phase, resulting in maximum illumination at point O1. On the other hand, at point O2, the distance BO2 is longer than the distance AO2. Therefore, by the time the two rays arrive at point O2, they are out of phase. Assuming that the phase difference d = λ/2, where λ is the wavelength of light, complete interference occurs, forming a dark spot.
At point O3 on the screen, the distance BO3 is longer than AO3. If the difference between the two distances, that is, BO3 − AO3, is equal to an even number of half wavelengths, the two light rays arriving at O3 will be in phase, leading to the formation of a bright spot. This process repeats on either side of O1 on the screen, resulting in the formation of alternate dark and bright areas. This pattern of alternate bright and dark areas is popularly known as fringes. The dark areas will occur whenever the path difference of A and B amounts to an odd number of half wavelengths, and the bright areas will occur when the path difference amounts to an even number of half wavelengths.
Conclusion
We have discussed the Optical Interference with schematic diagram. Please let us know your thought in the comment session below.

Great, did you conducted any experiments regarding optical technology.
I did not conducted any experiments on the optical technology. Thanks for the question.