A simple example of a Simple Harmonic Motion is when we stretch a spring with a mass and release, then the mass will oscillate back and forth. This oscillation is called the Simple harmonic motion. Let’s discuss this topic in detail with some other definitions related to the Simple Harmonic Motion.

Simple Harmonic Motion
As we said above as the oscillatory motion of the object is called the simple harmonic motion. Let’s elaborate on the topic with the example.
Let’s consider an object moving along the circumference of the circle in an anticlockwise direction with the constant angular velocity.
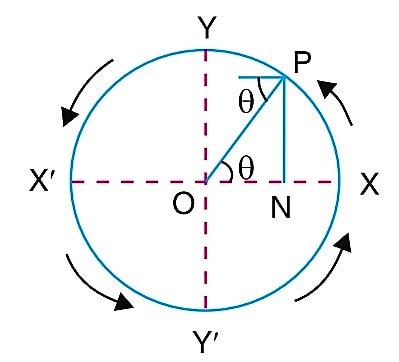
Let’s say the position of the object is P and N will be the projection of the object on the diameter XX’ of the circle as shown in the fig.
Now if the object P movies in the circumference path of the circle, then the projection of this object N will be moves in linear motion on XX’.
If the P moves from X to X’ along the circular path through the Y, then the projection point N will also move from X to X’ through O (centre of the circle). Hence each time the P completes one revolution, the N will also complete one vibration.
This to and fro motion of N is known as simple harmonic motion. We can also write this simple harmonic motion as SHM.
What are the Important terms used in the SHM?
- Amplitude
- Periodic time
- Frequency
Amplitude
The amplitude is the maximum displacement of a body from its mean position. In the above picture, the maximum can be the radius of the circle.
Periodic Time
Periodic time is the time taken for one complete revolution of the object on the circle.
Periodic time( tp) = 2π/ω seconds
Frequency
Frequency is defined as the number of cycles per second. It is the reciprocal of the time period. Units are Hertz. Written as Hz
Frequency (n) = ω/2π Hz
Displacement , Velocity and acceleration of the object moving with the simple harmonic motion.
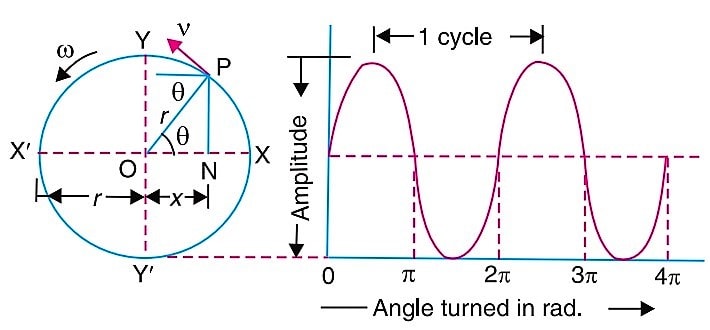
From the above consideration, the displacement is of N is x
x = r. cos θ (∵ From the triangle OPN, cos θ =x/r )
Where θ is the angle turned by the particle P in t seconds. which is θ = ω.t
x = r. cos ω.t
The velocity of the projection point N from its mean position O is
vN = v. sin θ
vN = ω.r sin θ (∵ v = ω.r )
vN = ω NP (∵ from Triangle OPN, sin θ = NP/r)
vN = ω (r2-x2)1/2 (∵ NP2 = r2-x2 from the right angle triangle NPO )
The maximum velocity will have occurred at position O
i.e x = 0 then
vmax = ω.r
The acceleration of the object P is the centripetal acceleration whose magnitude is ω2.r
The acceleration of object P parallel to XX ′ and is directed towards the centre O, i.e.,
aN = ω2.r cos θ
aN = ω2.x (∵ from above equation x = r cos θ )
The acceleration will be maximum when the object is at the position X or X”
i.e x = r
amax = ω2.r
From the above equations, we can say that the acceleration will be zero at the mean position O. The acceleration of N is proportional to the displacement of the N from its mean position O. It is always directed towards the mean position O.
So the N is said as it is in Simple Harmonic Motion.
Conclusion
We have discussed the Simple Harmonic Motion definition and few other related definitions. Also discussed the Displacement, velocity and the acceleration of the object when it is in simple harmonic motion. If you have any further thoughts on this topic, let us know in the comment section below.

If you want a more detailed discussion, consult any college physics textbook. A trig/algebra based book is just as good as a calculus based text. The calculus text gives a way to derive these equations and explains the applications of the first and second derivatives. That defines acceleration and velocity.