In Fluid Mechanics, a Water Hammer is a most seen phenomenon that can occur in any piping system where valves are used to control the flow of liquids or steam. Let us discuss the different causes of Water hammering and the different outcomes of Water Hammering.

Water Hammer in Pipes
A water hammer is the result of a pressure surge or high-pressure shockwave that propagates through a piping system when a fluid in motion is forced to change direction or stop abruptly.
Let us conduct a small experiment to illustrate the Water Hammer phenomenon in detail. consider a long pipe AB as shown in the following figure connected at one end to a tank containing water at a height of H from the centre of the pipe. At the other end of the pipe, a valve to regulate the flow of water is provided.
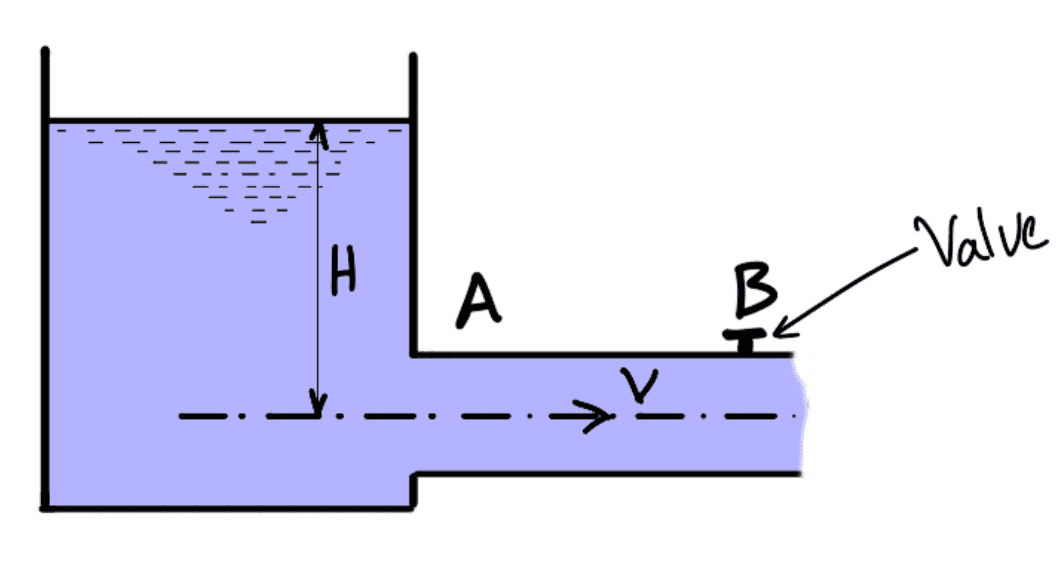
When the valve is completely open, the water is flowing with a velocity, V in the pipe. If now the valve is suddenly closed, the momentum of the flowing water will be destroyed and consequently, a wave of high pressure will be set up. This wave of high pressure will be transmitted along the pipe with a velocity equal to the velocity of the sound wave and may create a noise called knocking. Also, this wave of high pressure has the effect of hammering action on the walls of the pipe and hence it is also known as a water hammer.
The pressure rise due to water hammer depends upon
- The velocity of flow of water in the pipe
- Length of pipe
- Time is taken to close the valve
- Elastic properties of the material of the pipe
The following cases of water hammers in pipes will be considered :
- Gradual closure of the valve
- Sudden closure of valve and considering pipe rigid
- Sudden closure of valve and considering pipe elastic.
1. Gradual Closure of Valve
Let the water is flowing through pipe AB shown in the above figure, and the valve provided at the end of the pipe is closed gradually.
Let
A = area of cross-section of the pipe AB
L = length of pipe
V = velocity of flow of water through a pipe
T = time in the second required to close the valve
p = intensity of pressure wave produced.
Mass of water in pipe AB = ρ × volume of water = ρ × A × L
The valve is closed gradually in time “T’ seconds and hence the water is brought from initial velocity V to zero velocity in time seconds.
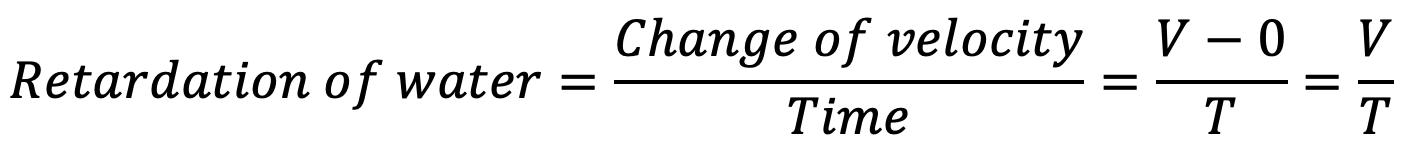
Retarding force = Mass × Retardation = ρAL × V ÷ L
If p is the intensity of the pressure wave produced due to closure of the valve, the force due to pressure wave = p × area of pipe = p × A
Equating the two forces, given by the above two equations, we get
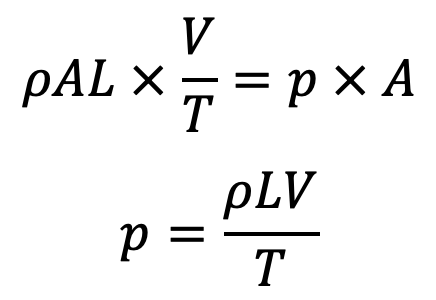
Head of pressure,
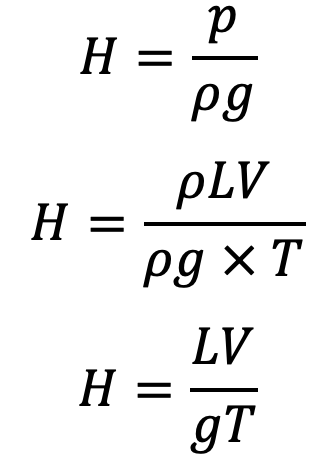
- (i) The valve closure is said to be gradual if T > 2L/C
where 1 = time in seconds, C = velocity of pressure wave - (ii) The valve closure is said to be sudden if T < 2L/C
where C = velocity of the pressure wave.
2. Sudden Closure of Valve and Pipe is Rigid
Equation (a) gives the relation between the increase of pressure due to the water hammer in the pipe and the time required to close the valve. If t = 0, the increase in pressure will be infinite. But from experiments, it is observed that the increase in pressure due to the water hammer is finite, even for very rapid closure of the valve.
Thus equation (a) is valid only for the following types of fluids.
(i) Incompressible fluids
(ii) When the pipe is rigid
But when a wave of high pressure is created, the liquids get compressed to some extent and also pipe material gets stretched. For a sudden closure of valve the valve of t is small and hence a wave of high pressure is created the following two cases will be considered:
- (i) Sudden closure of valve and pipe is rigid
- (ii) Sudden closure of valve and pipe is elastic
Consider a pipe AB in which water is flowing as shown in the above schematic diagram. Let the pipe is rigid and the valve fitted at the end B is closed suddenly.
Let
A = Area of the cross-section of pipe AB
L = Length of pipe
V = Velocity of the flow of water through the pipe
p = Intensity of pressure wave produced
K = Bulk modulus of water
When the valve is closed suddenly, the kinetic energy of the flowing water is converted into strain energy of water if the effect of friction is neglected and the pipe wall is assumed perfectly rigid.
Loss of kinetic energy = 1/2 × mass of water in pipe x V2
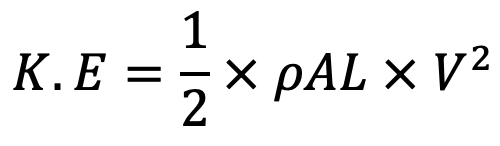
Gain of strain energy can be written as follows
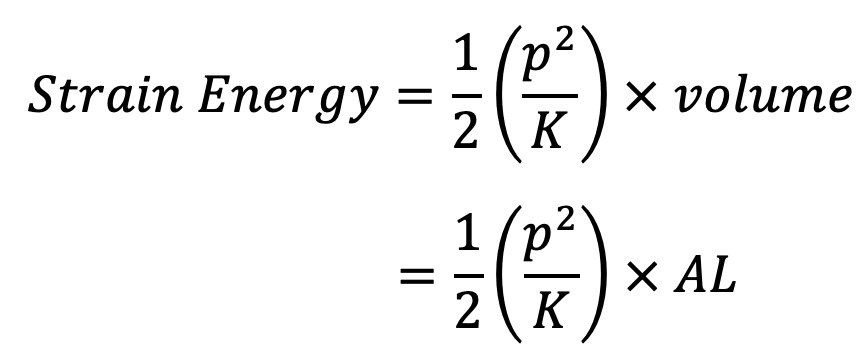
Equating loss of kinetic energy to gain of strain energy
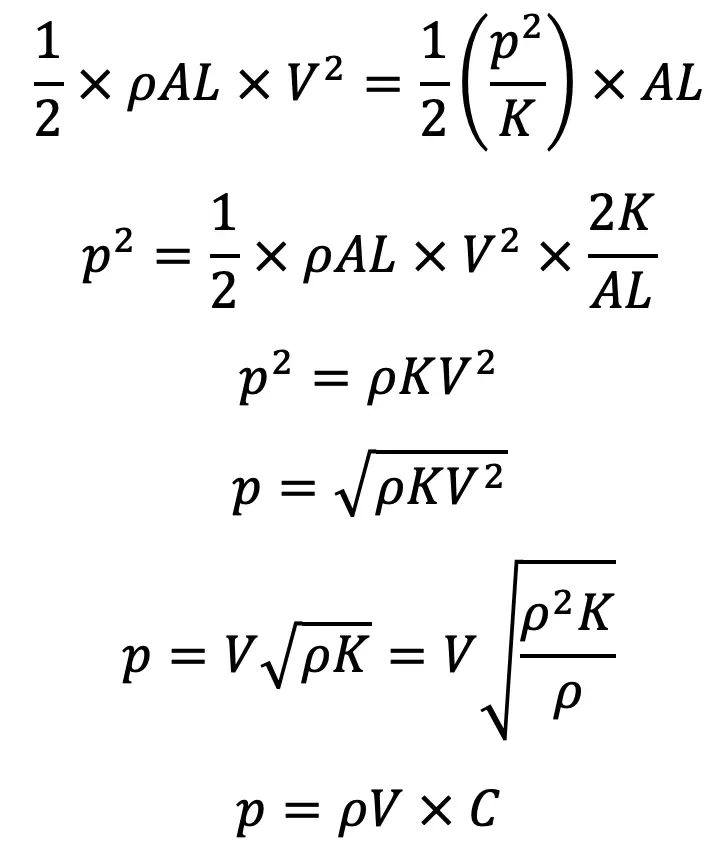
where C = velocity of the pressure wave.
3. Sudden Closure of Valve and Pipe is Elastic
Consider the pipe AB in which water is flowing as shown in the above schematic. Let the thickness ” of the pipe wall is small compared to the diameter D of the pipe and also let the pipe is elastic.
Let
E = Modulus of Elasticity of the pipe material
1/m = Poison’s ratio for pipe material
p = Increase of pressure due to water hammer
t = Thickness of the pipe wall
D = Diameter of the pipe
When the valve is closed suddenly, a wave of high pressure of intensity p will be produced in the water. Due to this high-pressure p, circumferential and longitudinal stresses in the pipe wall will be produced.
Let
fl = Longitudinal stress in the pipe
fc = Circumferential stress in the pipe
The magnitude of these stresses is given as
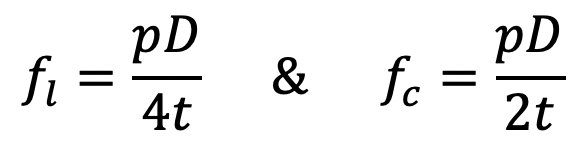
Now from the knowledge of strength of material we know, strain energy stored in pipe material per unit volume

Strain energy stored in pipe material per unit volume
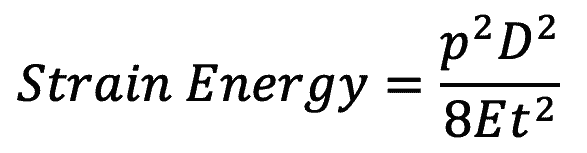
The total volume of pipe material = πD × t × L
Total strain energy stored in pipe material = Strain energy per unit volume × total volume
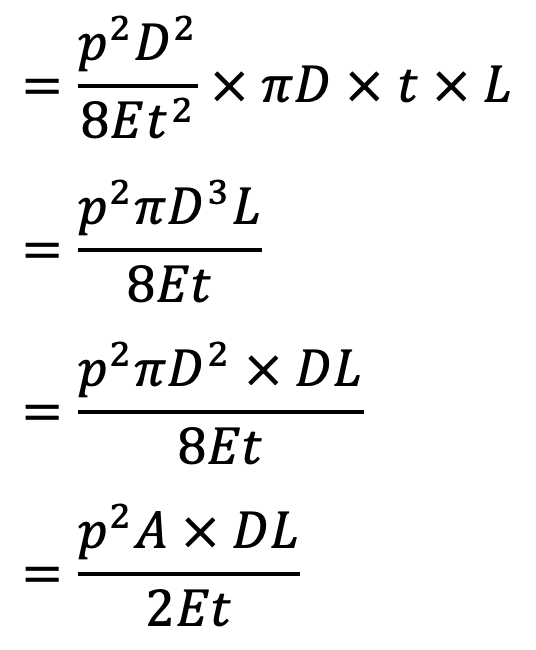
Now the loss of kinetic energy of water =
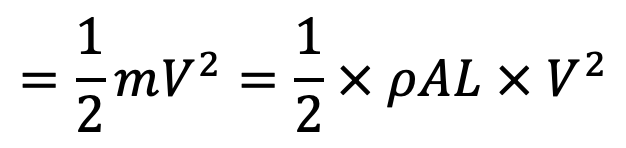
Then, loss of kinetic energy of water = Gain of strain energy in water + Strain energy stored in pipe material.
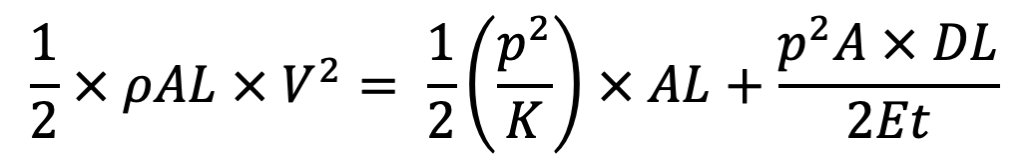
Cancelling AL on both sides, we get
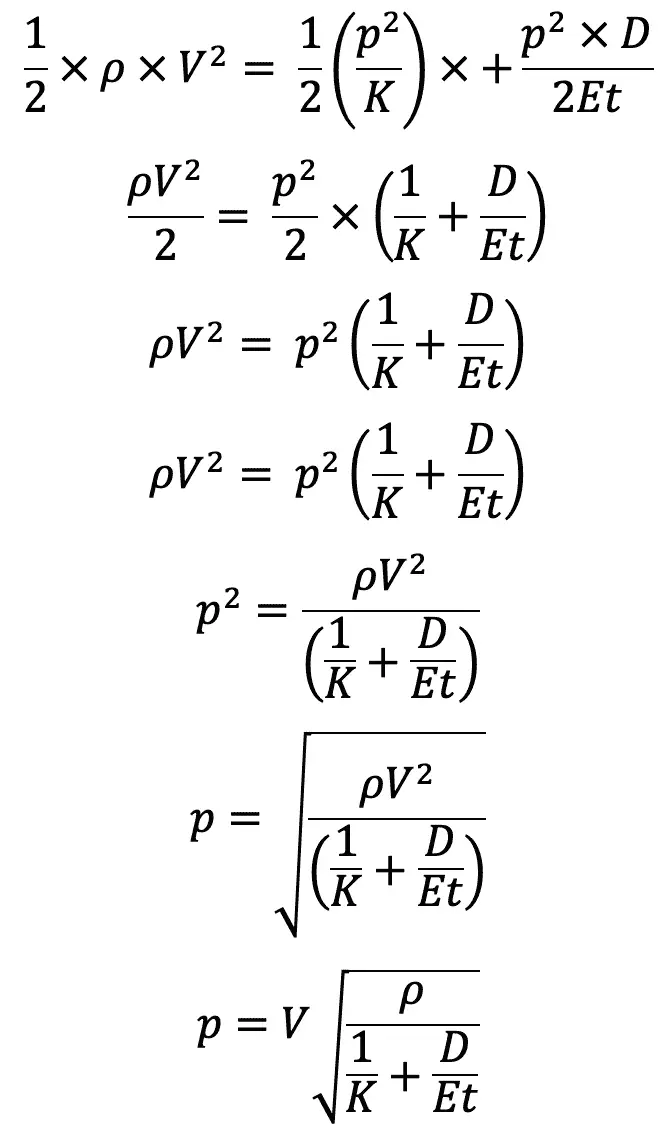
This is the relation to determine the Increase of pressure due to water hammer in pipes.
Time Taken by Pressure Wave to Travel from the Valve to the Tank and from Tank to the Valve
Let
T = The required time is taken by the pressure wave
L = Length of the pipe
C = Velocity of pressure wave
The total distance = L+ L = 2L
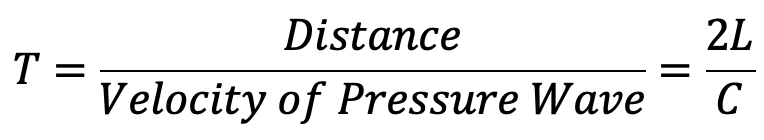
This is all about the Water Hammer In Pipes. Let us know what you think about this article in the comment section below.

Leave a Reply