What are Flat Spiral Spring?

A spring is defined as an elastic body, whose function is to distort when loaded and to recover its original shape when the load is removed. It absorbs or controls energy due to either shock or vibration so it can be used as shock absorbers and vibration dampers. It is also used to apply forces, as in brakes, clutches, and spring-loaded valves. We have already discussed different types of springs in the previous article. Let us discuss about the Flat Spiral Spring.

Applications of Springs

The various important applications of springs are as follows:

1. To cushion, absorb, or control energy due to either shock or vibration as in car springs, railway buffers, aircraft landing gears, shock absorbers, and vibration dampers.
2. To apply forces, as in brakes, clutches, and spring-loaded valves.
3. To control motion by maintaining contact between two elements as in cams and followers.
4. To measure forces, as in spring balances and engine indicators.
5. To store energy, as in watches, toys, etc.

Types of Springs

Though there are many types of springs, the following, according to their shape, are important from the subject point of view.

• Helical springs
• Conical and volute springs
• Torsion springs
• Laminated or leaf springs
• Disc or Belleville springs
• Special-purpose springs

We have discussed more details in a separate article here!

Flat Spiral Spring

A flat spring is a long thin strip of elastic material wound like a spiral as shown in the following figure. These springs are frequently used in watches and gramophones etc.

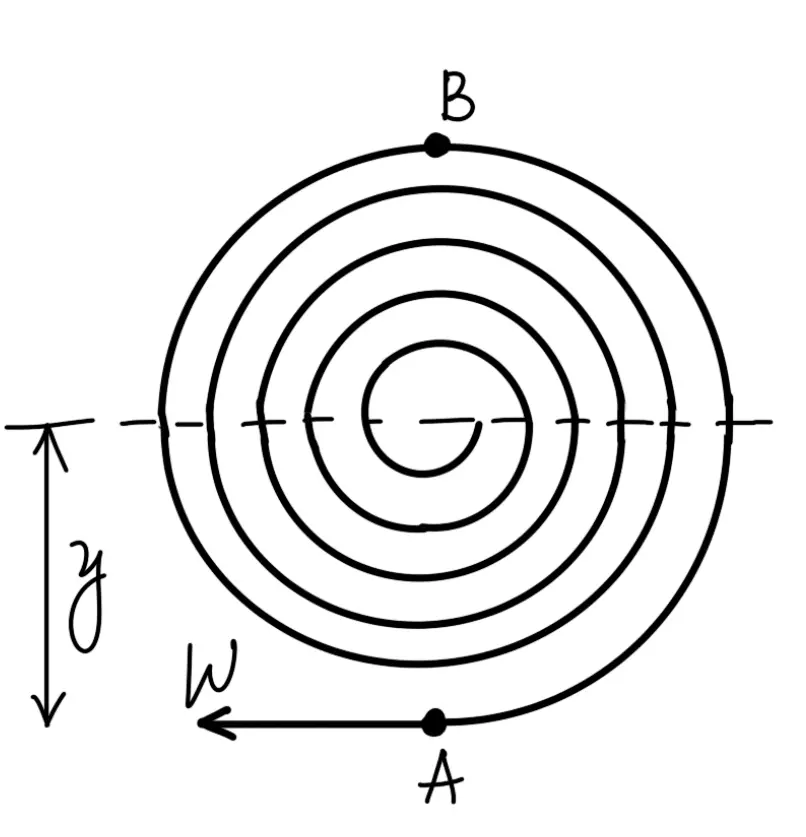
When the outer or inner end of this type of spring is wound up in such a way that there is a tendency to the increase number of spirals of the spring, the strain energy is stored in its spirals. This energy is utilized in any useful way while the spirals open out slowly. Usually, the inner end of the spring is clamped to an arbor while the outer end may be pinned or clamped. Since the radius of curvature of every spiral decreases when the spring is wound up, therefore the material of the spring is in a state of pure bending.

Let
W = Force applied at the outer end A of the spring
y = Distance of centre of gravity of the spring from A
l = Length of the strip forming the spring
b = Width of strip
t = Thickness of strip,
I = Moment of inertia of the spring section = b.t³/12
Z = Section modulus of the spring section = b.t³/6

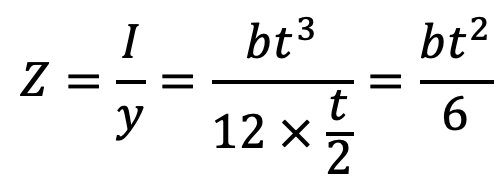
When the end A of the spring is pulled up by a force W, then the bending moment on the spring, at a distance y from the line of action of W is given by

M = W × y

The greatest bending moment occurs in the spring at B which is at a maximum distance from the application of W.

∴ Bending moment at B is

M_B = M_max = W × 2y = 2 W . y = 2M

Maximum bending stress induced in the spring material,

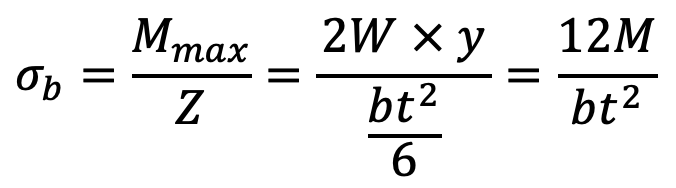
Assuming that both ends of the spring are clamped, the angular deflection (in radians) of the spring is given by

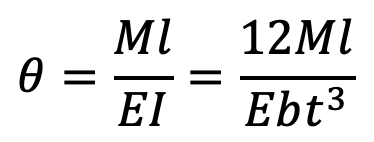
and the deflection,

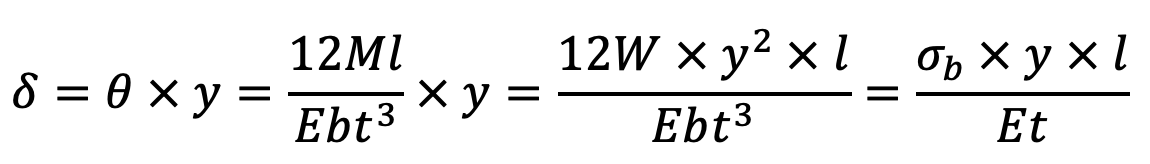
The strain energy stored in the spring

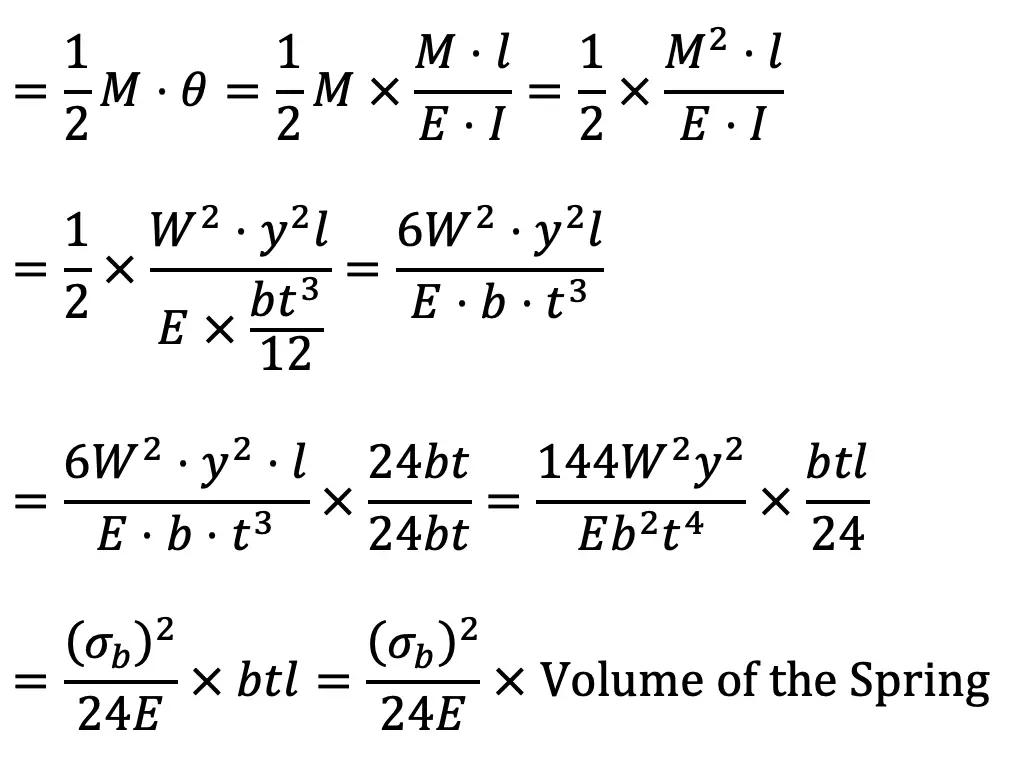
How to calculate the strain energy stored in the spiral spring?

Problem Statement: A spiral spring is made of a flat strip 6 mm wide and 0.25 mm thick. The length of the strip is 2.5 metres. Assuming the maximum stress of 800 MPa to occur at the point of greatest bending moment, calculate the bending moment, the number of turns to wind up the spring and the strain energy stored in the spring. Take E = 200 kN/mm².

Answer:

width of the spring strip b = 6 mm ; 
Thickness of the soring strio t = 0.25 mm ; 
Length of the strip l = 2.5 m = 2500 mm ; 
Maximum stress τ = 800 MPa = 800 N/mm2 ; 
modulus of elasticity E = 200 kN/mm2 = 200 × 103 N/mm²

Bending moment in the spring

Let
M = Bending moment in the spring

We know that the maximum bending stress in the spring material (σ_b),

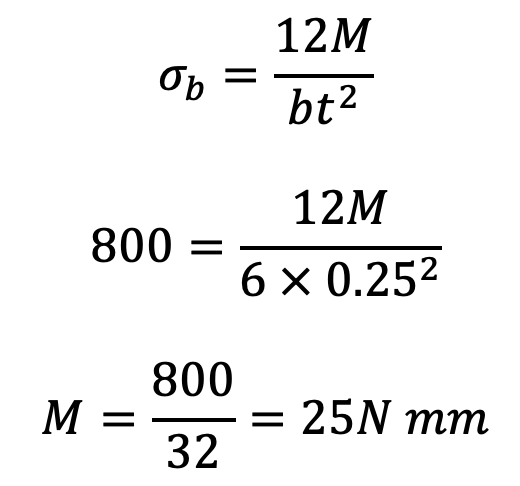
Number of turns to wind up the spring

We know that the angular deflection of the spring,

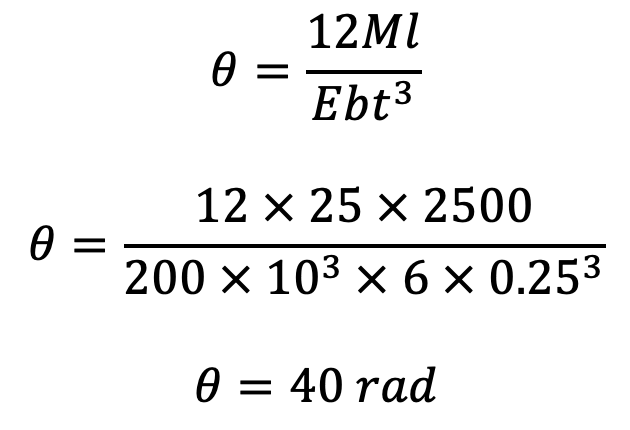
Since one turn of the spring is equal to 2π radians, therefore number of turns to wind up the spring

= 40 / 2π = 6.36 turns

Strain energy stored in the spring

We know that strain energy stored in the spring

= (1/2) M . θ = (1 / 2) × 24 × 40 = 480 N-mm

This is all about the Flat Spiral Springs and how we calculate the strain energy stored in the spiral spring. Let us know what you think about this article in the comment section.