Most elemental metals about 90% crystallize upon solidification into three densely packed crystal structures. Those are body-centered cubic (BCC), face-centered cubic (FCC), and hexagonal close-packed (HCP). Let us discuss these Principal Metallic Crystal Structures in detail.

Important Definitions
👉 Crystal: is a solid composed of atoms, ions, or molecules arranged in a pattern that is repetitive in three dimensions.
👉 Crystal Lattice/space Lattice: is an atomic arrangement of the constituent atoms or ions or molecules to the points of intersection of a network of lines in three dimensions space.
👉 Unit Cell: is the smallest replicating portion of a crystal lattice
👉 Crystal Structure: the particular repeating arrangement of atoms throughout a crystal. A unit cell is a building block of the Crystal structure. The crystal structure is made of atoms. A crystal lattice is made of points.
Principal Metallic Crystal Structures
The HCP structure is a denser modification of the simple hexagonal crystal structure. Most metals crystallize in these dense-packed structures because energy is released as the atoms come closer together and bond more tightly with each other. Thus, the densely packed structures are in lower and more stable energy arrangements.
The extremely small size of the unit cells of crystalline metals that are shown below should be emphasized.
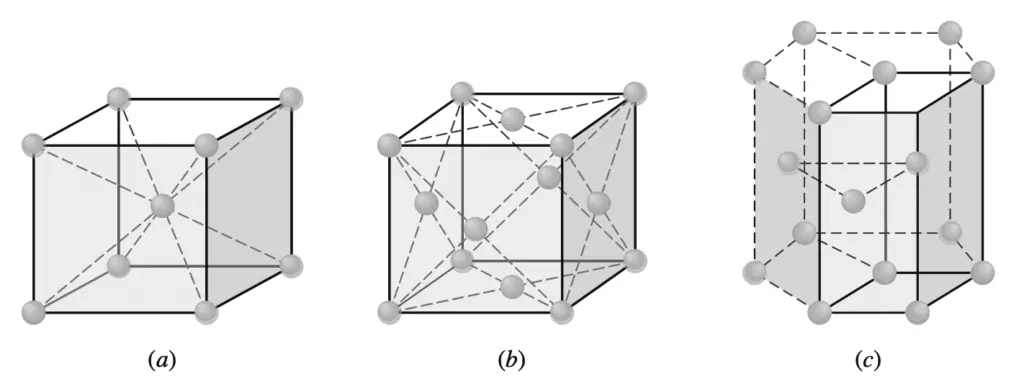
(a) Body-centered cubic
(b) Face-centered cubic
(c) Hexagonal close-packed
(the unit cell is shown by solid lines).
The cube side of the unit cell of body-centered cubic iron, for example, room temperature is equal to 0.287 × 10−9 m, or 0.287 nanometers (nm).
Therefore, if unit cells of pure iron are lined up side by side, in 1 mm there will be
1 mm × 1 unit cell / (0.287 nm × 10−6 mm/nm = 3.48 × 106 unit cells!
Let us now examine in detail the arrangement of the atoms in the three principal crystal structure unit cells. Although an approximation, we shall consider atoms in these crystal structures to be hard spheres.
The distance between the atoms (interatomic distance) in crystal structures can be determined experimentally by X-ray diffraction analysis.
For example, the interatomic distance between two neighboring aluminum atoms in a piece of pure aluminum at 20°C is 0.286 nm.
The radius of the aluminum atom in the aluminum metal is assumed to be half the interatomic distance
of 0.143 nm. The atomic radii of selected metals are listed in Tables respectively for the BCC, FCC, and HCP.
1. Body-Centered Cubic (BCC) Crystal Structure
First, consider the atomic-site unit cell for the BCC crystal structure shown below in Figure.
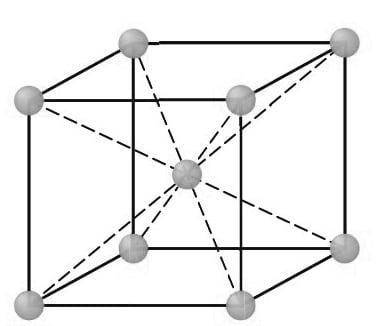
In this unit cell, the solid spheres represent the centers where atoms are located and clearly indicate their relative positions. If we represent the atoms in this cell as hard spheres, then the unit cell appears as shown below.
In this unit cell, we see that the central atom is surrounded by eight nearest neighbors and is said to have a coordination number of 8.
If we isolate a single hard-sphere unit cell, we obtain the model shown below. Each of these cells has the equivalent of two atoms per unit cell. One complete atom is located at the center of the unit cell, and an eighth of a sphere (an octant) is located at each corner of the cell, making the equivalent of another atom.
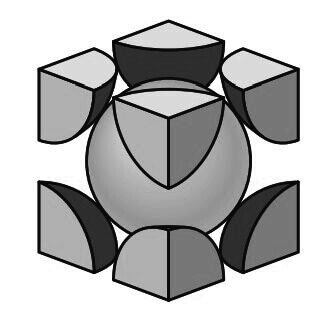
BCC unit cells: (a) atomic-site unit cell, (b) hard-sphere unit cell, and(c) isolated unit cell.
Thus, there is a total of 1 (at the center) + 8 × 1/ 8 (at the corners) = 2 atoms per unit cell.
The atoms in the BCC unit cell contact each other across the cube diagonal, as indicated below figure, so the relationship between the length of the cube side a and the atomic radius R is
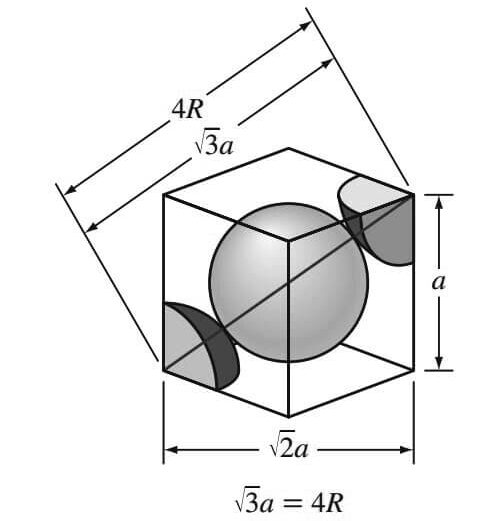
√(3a) = 4R
a = 4R/√3
Let us solve an example problem to find the Lattice constant of iron with BCC structure.
Example Problem to calculate Lattice Constant of BCC structure
Iron at 20°C is BCC with atoms of atomic radius 0.124 nm. Calculate the lattice constant a for the cube edge of the iron unit cell.
Answer:
From the below figure, it is seen that the atoms in the BCC unit cell touch across the cube diagonals.

Thus, if a is the length of the cube edge, then
√(3a) = 4R
Where R is the radius of the iron atom.
Therefore, considering that three significant digits should be used in all calculations, the answer will be
a = 4R /√3
a = 4(0.124 nm) /√3
a = 0.287 nm
The lattice constant of the Iron with BCC structure at 20°C is 0.287 nm.
The following table shows the lattice constants and atomic radii of selected metals that have the BCC crystal structure at room temperature (20°C)
| Metal | Lattice Constant a (nm) | Atomic Radius R* (nm) |
| Chromium | 0.289 | 0.125 |
| Iron | 0.287 | 0.124 |
| Molybdenum | 0.315 | 0.136 |
| Potassium | 0.533 | 0.231 |
| Sodium | 0.429 | 0.186 |
| Tantalum | 0.33 | 0.143 |
| Tungsten | 0.316 | 0.137 |
| Vanadium | 0.304 | 0.132 |
*Calculated from lattice constants by using Eqn, R = √3 a/4.
If the atoms in the BCC unit cell are considered to be spherical, an atomic packing factor (APF) can be calculated by using the following equation
APF = volume of atoms in unit cell /volume of the unit cell
Using this equation, the APF for the BCC unit cell can be calculated.
Let us solve an example problem to calculate the Atomic Packing Factor (APF) for the BCC unit cell.
Example Problem to Calculate Atomic Packing Factor (APF) for the BCC Structure
Calculate the atomic packing factor (APF) for the BCC unit cell, assuming the atoms to be hard spheres
Answer:
We know the Formula for Atomic Packing Factor (APF) for the BCC Structure
APF = volume of atoms in BCC unit cell /volume of BCC unit cell
Since there are two atoms per BCC unit cell, the volume of atoms in the unit cell of radius R is
Vatoms = (2) ( (4/3) πR3 ) = 8.373R3
The volume of the BCC unit cell is Vunit cell = a3
where a is the lattice constant.
The relationship between a and R is obtained from the above figure.
which shows that the atoms in the BCC unit cell touch each other across the cubic diagonal. Thus,
√(3a) = 4R
a = 4R/√3
Thus,
Vunit cell = a3 = 12.32R3
The atomic packing factor for the BCC unit cell will be
APF = Vatoms/unit cell /Vunit cell
APF = 8.373R3 /12.32R3
APF = 0.6796 ≈ 0.68
the APF for the BCC unit cell is 68%.
That is, 68% of the volume of the BCC unit cell is occupied by atoms and the remaining 32% is empty space.
The BCC crystal structure is not a close-packed structure since the atoms could be packed closer together.
Many metals such as iron, chromium, tungsten, molybdenum, and vanadium have the BCC crystal structure at room temperature.
2. Face-Centered Cubic (FCC) Crystal Structure
Consider next the FCC lattice-point unit cell of the below figure.
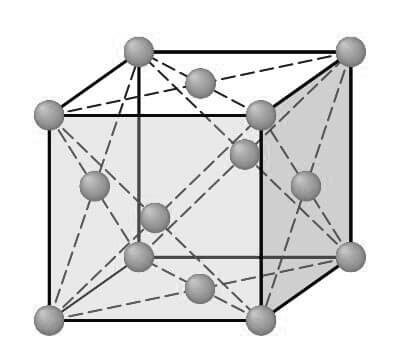
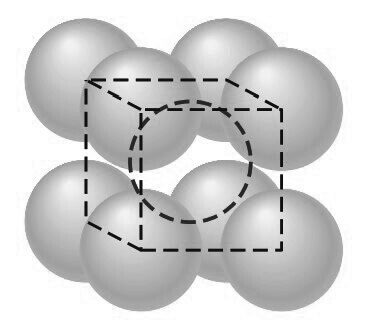
In this unit cell, there is one lattice point at each corner of the cube and one at the center of each cube face. The hard-sphere model of the Figure shown below indicates that the atoms in the FCC crystal structure are packed as close together as possible, and are thus called a close-packed structure.
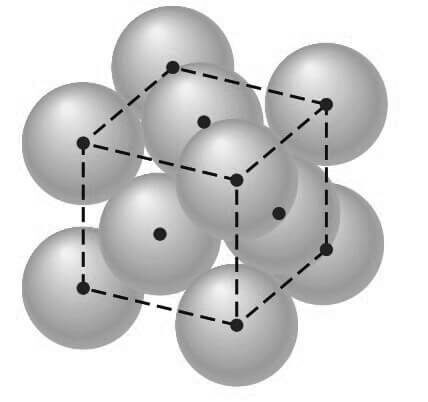
The APF for this close-packed structure is 0.74 as compared to 0.68 for the BCC structure, which is not close-packed.
The FCC unit cell has the equivalent of four atoms per unit cell as shown in the below figure.
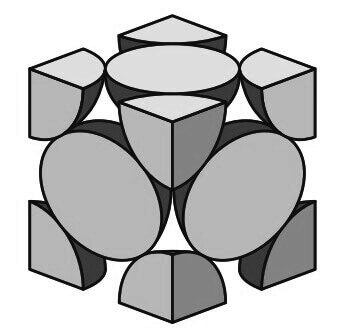
The eight corner octants account for one atom (8 × 1/8 = 1)
The six half atoms on the cube faces contribute another three atoms, making a total of four atoms per unit cell.
The atoms in the FCC unit cell contact each other across the cubic face diagonal, as indicated in below Figure.
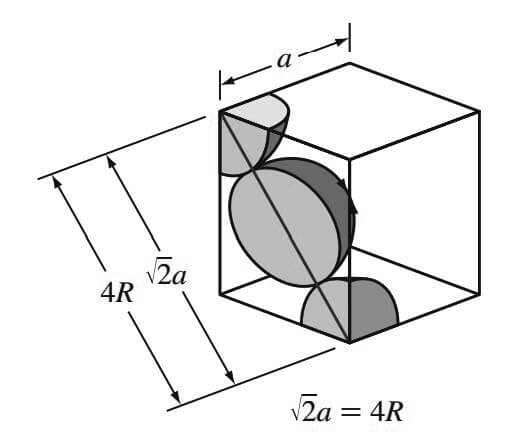
So the relationship between the length of the cube side a and the atomic radius R is
√2a = 4R
a = 4R / √2
Since the atoms touch across the face diagonals,
√/2a = 4R
We can find the atomic packing factor for the FCC structure similar to what we did for the BCC structure above.
The APF for the FCC crystal structure is 0.74, which is greater than the 0.68 factor for the BCC structure.
The APF of 0.74 is for the closest packing possible of “spherical atoms.” Many metals such as aluminum, copper, lead, nickel, and iron at elevated temperatures (912°C to 1394°C) crystallize with the FCC crystal structure.
The following table lists the lattice constants and atomic radii for some selected FCC metals.
| Metal | Lattice Constant a (nm) | Atomic Radius R* (nm) |
| Aluminum | 0.405 | 0.143 |
| Copper | 0.3615 | 0.128 |
| Gold | 0.408 | 0.144 |
| Lead | 0.495 | 0.175 |
| Nickel | 0.352 | 0.125 |
| Platinum | 0.393 | 0.139 |
| Silve | 0.409 | 0.144 |
*Calculated from lattice constants by using the above equation, R = √2a/4.
3. Hexagonal Close-Packed (HCP) Crystal Structure
The third common metallic crystal structure is the hexagonal close-packed (HCP) structure shown below.
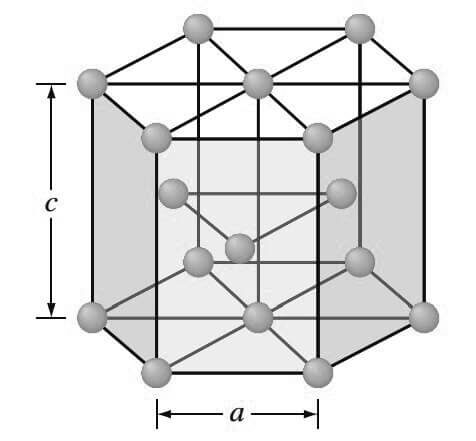
Metals do not crystallize into the simple hexagonal crystal structure because the APF is too low.
The atoms can attain lower energy and a more stable condition by forming the HCP structure as shown in the below figure.
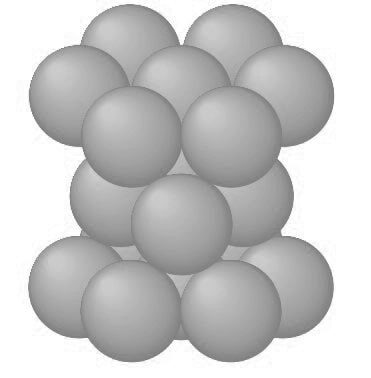
The APF of the HCP crystal structure is 0.74, the same as that for the FCC crystal structure since in both structures the atoms are packed as tightly as possible.
In both the HCP and FCC crystal structures, each atom is surrounded by 12 other atoms, and thus both structures have a coordination number of 12.
The isolated HCP unit cell, also called the primitive cell, is shown in the below figure.
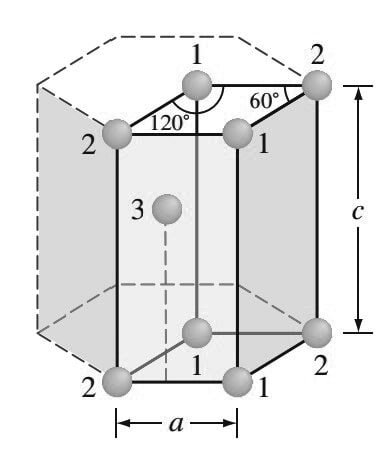
The atoms at locations marked “1” contribute 1/6 of an atom to the unit cell.
The atoms at locations marked “2” contribute 1/12 of an atom to the unit cell.
Thus, the atoms at the eight corners of the unit cell collectively contribute one atom (4(1/6 ) + 4(1/12 ) = 1).
- The atom at location “3” is centered inside the unit cell but extends slightly beyond the boundary of the cell.
- The total number of atoms inside an HCP unit cell is, therefore, two (one at corners and one at center).
- In some cases, the HCP unit cell is represented as first figure (schematic of the crystal structure)above and is called the “larger cell.”
- In such a case, one finds six atoms per unit cell. This is mostly for convenience, and the true unit cell is presented in an isolated unit cell schematic by the solid lines.
- When presenting the topics of crystal directions and planes we will also use the larger cell for convenience, in addition to the primitive cell.
- The ratio of the height c of the hexagonal prism of thSelected metals that have the HCP crystal structure at room temperature (20°C) and
- their lattice constants, atomic radii, and c/a ratiose HCP crystal structure to its basal side a is called the c/a ratio.
The c/a ratio for an ideal HCP crystal structure consisting of uniform spheres packed as tightly together as possible is 1.633.
The following table lists some important HCP metals and their c/a ratios.
| Metal | Lattice Constants (nm) a | Lattice Constants (nm) c | Atomic Radius R (nm) | c/a Ratio | % Deviation a c from Ideality |
| Cadmium | 0.2973 | 0.5618 | 0.149 | 1.89 | 15.7 |
| Zinc | 0.2665 | 0.4947 | 0.133 | 1.856 | 13.6 |
| Ideal HCP | – | – | – | 1.633 | 0 |
| Magnesium | 0.3209 | 0.5209 | 0.16 | 1.623 | −0.66 |
| Cobalt | 0.2507 | 0.4069 | 0.125 | 1.623 | −0.66 |
| Zirconium | 0.3231 | 0.5148 | 0.16 | 1.593 | −2.45 |
| Titanium | 0.295 | 0.4683 | 0.147 | 1.587 | −2.81 |
| Beryllium | 0.2286 | 0.3584 | 0.113 | 1.568 | −3.98 |
The metals listed, cadmium and zinc have c/a ratios higher than the ideal ratio, which indicates that the atoms in these structures are slightly elongated along the c axis of the HCP unit cell.
The metals magnesium, cobalt, zirconium, titanium, and beryllium have c/a ratios less than the ideal ratio. Therefore, in these metals, the atoms are slightly compressed in the direction along the c axis. Thus, for the HCP metals listed in the above table, there is a certain amount of deviation from the ideal hard-sphere model.
Let us solve an example problem to calculate the Volume of a metal which consists of an HCP crystal structure.
Example problem to Calculate Volume of a metal which consists of an HCP crystal structure
Calculate the volume of the zinc crystal structure unit cell by using the following data: pure zinc has the HCP crystal structure with lattice constants a = 0.2665 nm and c = 0.4947 nm. Also, Find the volume of the larger cell.
Answer:
The volume of the zinc HCP unit cell can be obtained by determining the area of the base of
the unit cell and then multiplying this by its height, this is shown in the below figure.
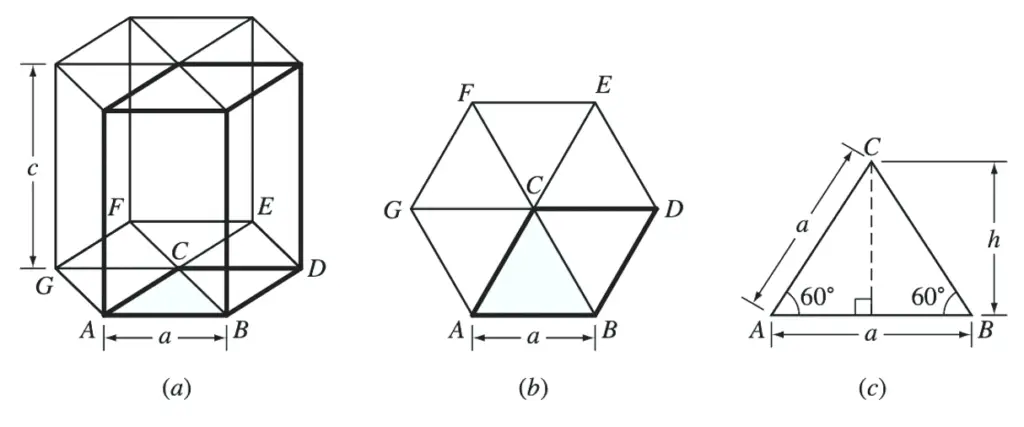
(a) HCP unit cell. (b) The base of the HCP unit cell. (c) Triangle ABC removed from the base of the unit cell
The area of the base of the unit cell is area ABDC of Figures a and b.
This total area consists of the areas of two equilateral triangles of area ABC of Figure b.
From Figure above example problem figure,
Area of triangle ABC = 1/2 (base)(height)
Area of triangle ABC = 1/2 (a)(a sin 60⚬)
Area of triangle ABC =1/2 a2 sin 60⚬
From Figure b,
Total area of HCP base, area ABDC = (2)(1/2 a2 sin 60⚬ )
Total area of HCP base, area ABDC = a2 sin 60⚬
From Figure a,
Volume of zinc HCP unit cell = ( a2 sin 60⚬ )(c)
= (0.2665 nm)2(0.8660 )(0.4947 nm)
= 0.03043 nm3
From Figure a,
Volume of “large” zinc HCP cell = 3(volume of the unit cell or primitive cell)
= 3(0.0304)
= 0.09130 nm3
Conclusion
The Principal Metallic Crystal Structures BCC, FCC, and HCP are discussed briefly and also discussed examples of how to calculate the atomic packing factors for BCC, FCC, and HCP. Also discussed is how to calculate the volume of metals with HCP structure. Let us know what do you think about these Principal Metallic Crystal Structures in the comment section below.

Leave a Reply