We have discussed different types of free vibrations (Longitudinal, Transverse, Torsional) in the previous article. In this article, we are going to discuss the Natural Frequency of Free Longitudinal Vibrations.

The natural Frequency of the Free Longitudinal Vibrations can be determined by the following methods.
- Equilibrium Method
- Energy Method
- Rayleigh’s method
Equilibrium Method
Let us consider a spring with a mass in unstrained position as shown in the below fig. We assume that the mass of the spring is negligible.
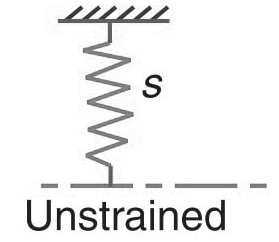
- s = Stiffness of the constraint. It is the force required to produce unit displacement in the direction of vibration. It is usually expressed in N/m.
- m = Mass of the body suspended from the constraint in kg,
- W = Weight of the body in newtons = m.g
- δ = Static deflection of the spring in metres due to weight W newtons
Now, let’s see the body is in the equilibrium position, the gravitational pull W = m.g, is balanced by a force of spring,
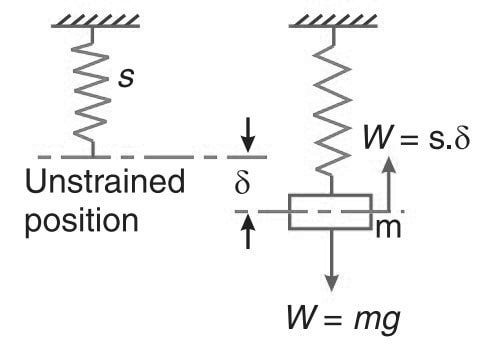
such that W = s. δ
Let’s give a displacement to the mass m by a distance x from its equilibrium position. This is shown in the below fig.
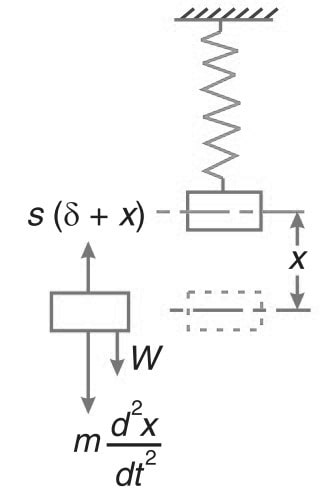
The restoring force will be
=W-s(δ+ x)
=W-sδ-sx
= – s.x ( ∵ W = s. δ)
Taking upward force as negative
Accelerating force = Mass × Acceleration
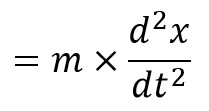
Taking downward force as positive.
From the above two equations of motion of the body of mass m after time t is given by
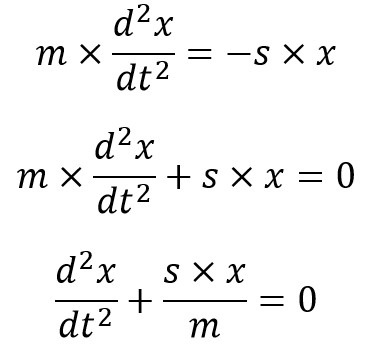
From the fundamental equation of the simple harmonic motion of the body is
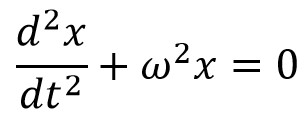
So equating these two similar equations will get us
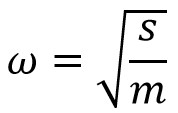
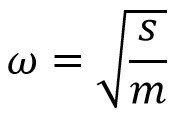
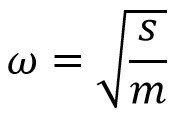
∴ Time period
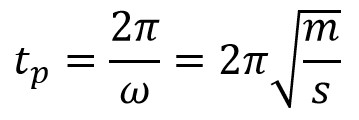
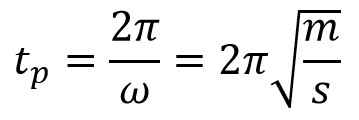
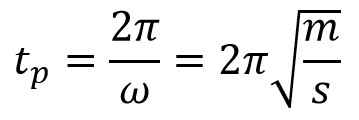
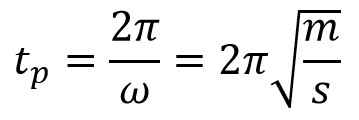
The natural frequency
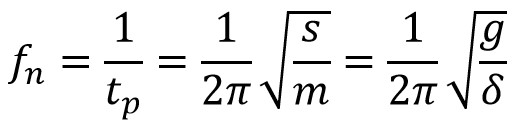
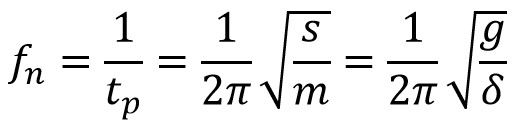
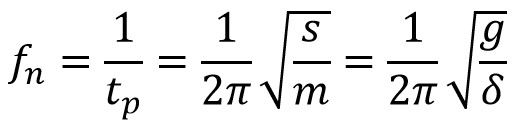
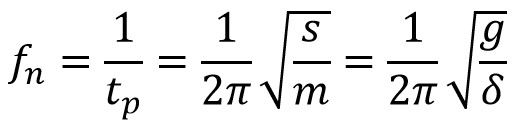
where mg = s δ
We knew that the value of g is 9.81 m/s2 and δ in metres,
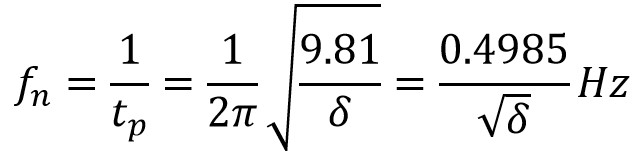
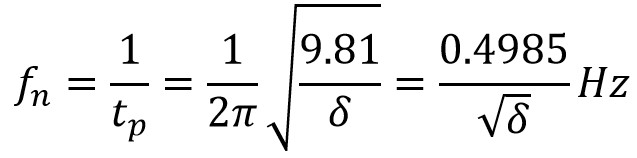
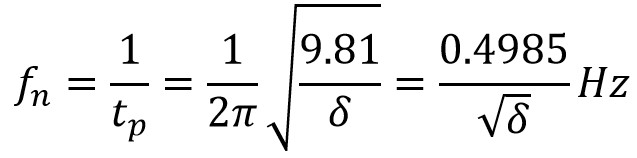
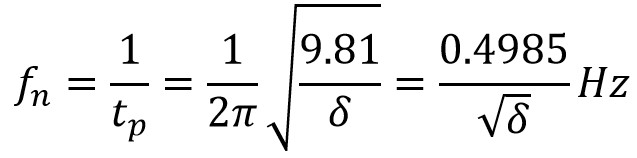
Where the δ is the static deflection (Extension or compression of the constraint)
This can be determined from the following equations
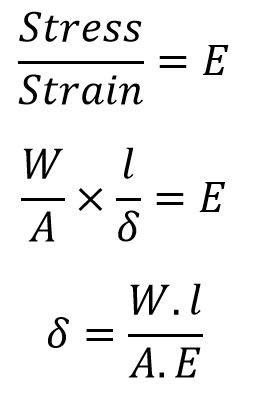


Where
- W = Load attached to the free end of constraint
- l = Length of the constraint
- E = Young’s modulus for the constraint
- A = Cross-sectional area of the constraint
Energy Method
In the free vibrations, no energy is transferred to the system or from the system, so that the total summation of the Kinetic energy and the potential energy of the system must be a constant quantity which is same at all the times.
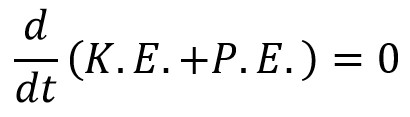
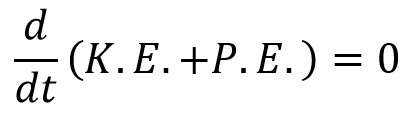
We knew kinetic energy and potential energy respectively,
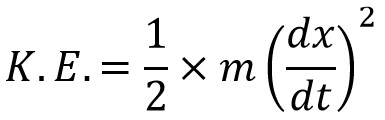
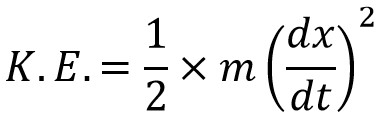
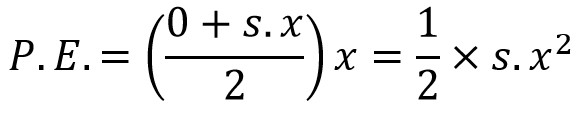
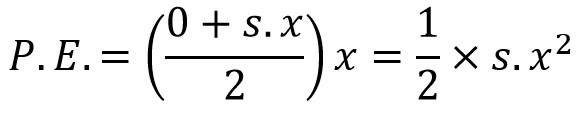
Now, we can substitute these two equations in the above equation.
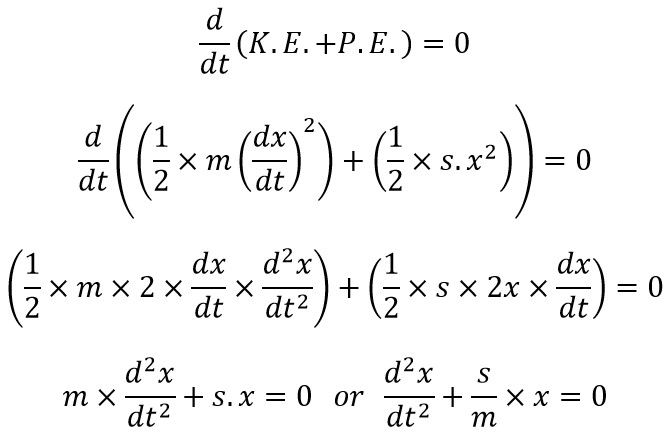
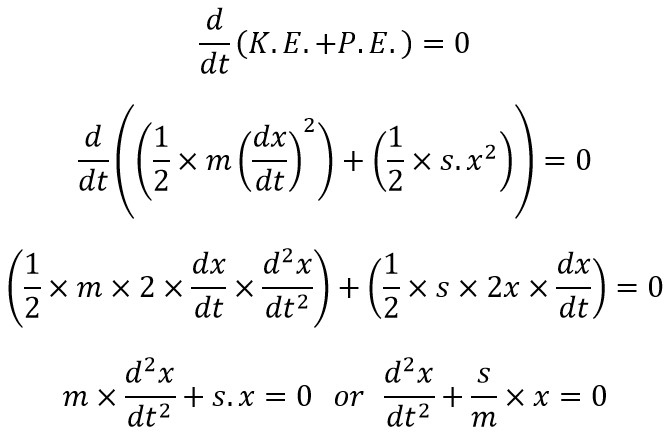
From the fundamental equation of the simple harmonic motion of the body is
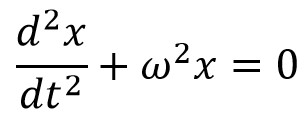
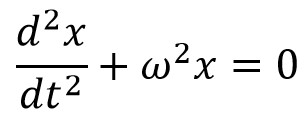
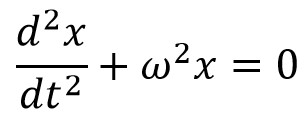
So equating these two similar equations will get us
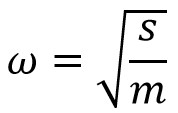
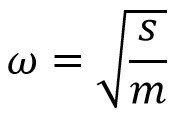
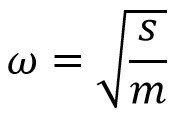
∴ Time period
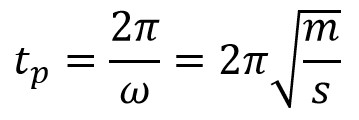
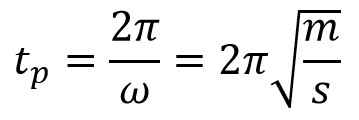
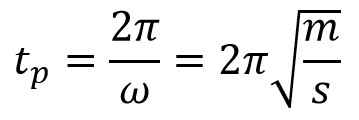
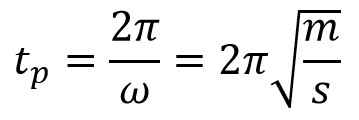
The natural frequency
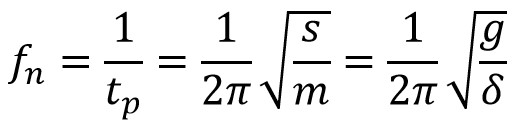
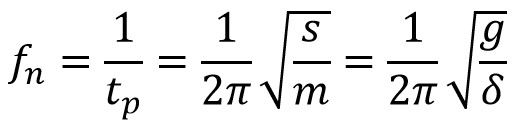
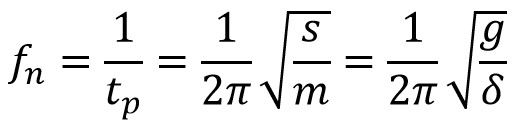
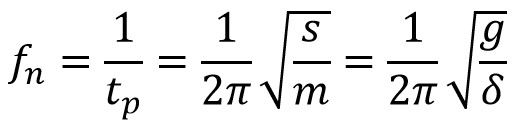
where mg = s δ
We knew that the value of g is 9.81 m/s2 and δ in metres,
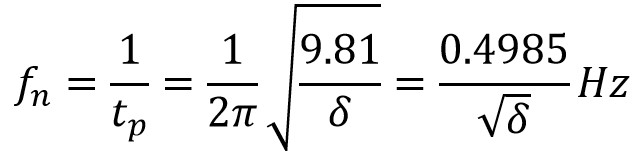
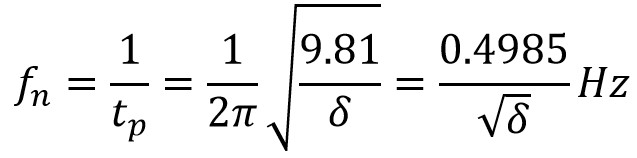
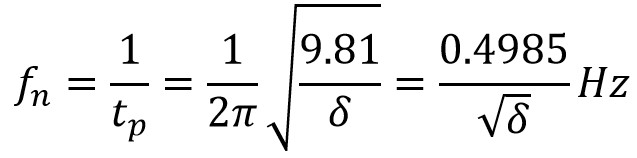
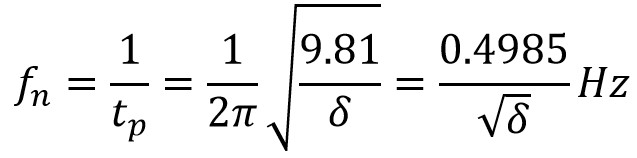
Where the δ is the static deflection (Extension or compression of the constraint)
This can be determined from the following equations
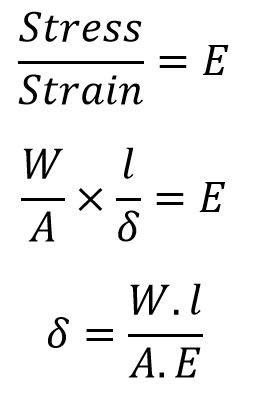


Where
- W = Load attached to the free end of constraint
- l = Length of the constraint
- E = Young’s modulus for the constraint
- A = Cross-sectional area of the constraint
Rayleigh’s Method
The maximum kinetic energy at the mean position is equal to the maximum potential energy or also called as the strain energy at the extreme position.
Assuming the motion executed by the vibration to be simple harmonic then,
x = X sin ω.t
Where
- x = Displacement of the body from the mean position after time t seconds,
- X = Maximum displacement from mean position to an extreme position
Differentiating the equation x = X sin ω.ton both sides,
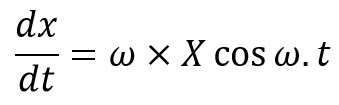
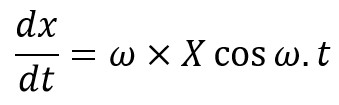
Since at the mean position, t = 0, therefore maximum velocity at the mean position
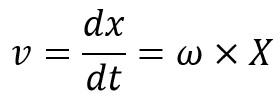
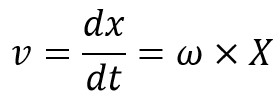
The maximum Kinetic energy at mean position
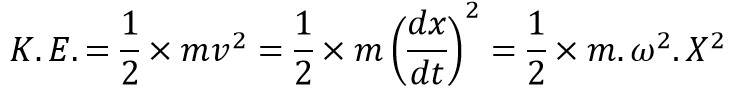
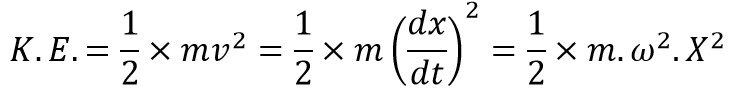
Also, The maximum potential energy at the extreme position
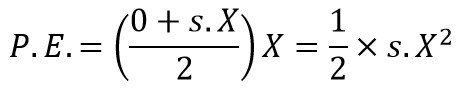
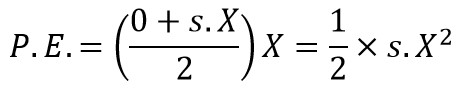
as we said the maximum kinetic energy at the mean position is equal to the maximum potential energy or also called as the strain energy at the extreme position. Equating above two equations,
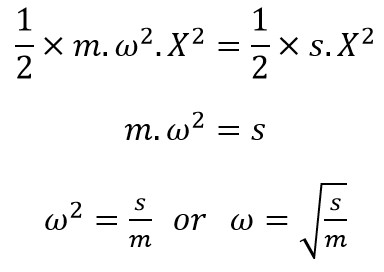
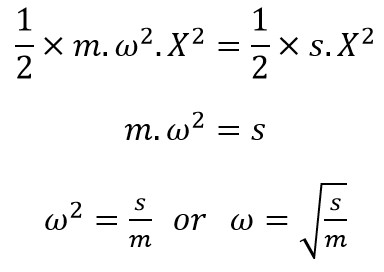
∴ Time period
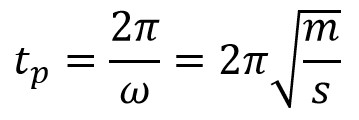
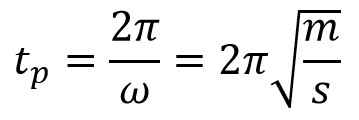
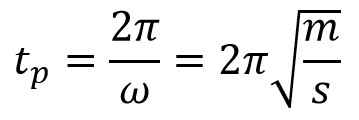
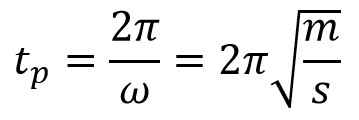
The natural frequency
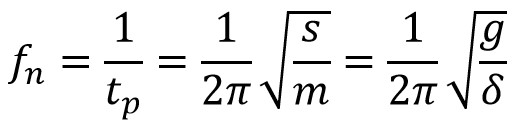
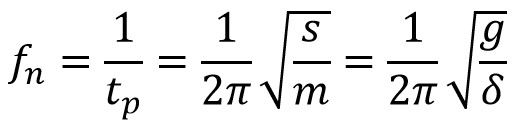
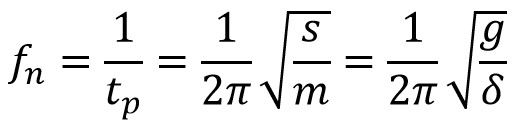
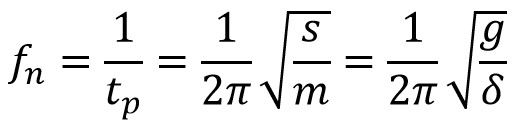
where mg = s δ
We knew that the value of g is 9.81 m/s2 and δ in metres,
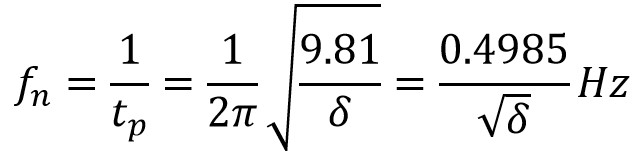
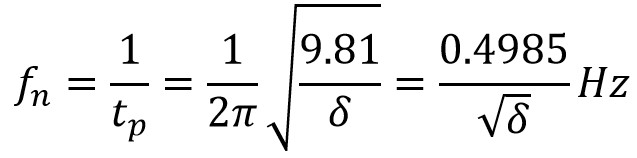
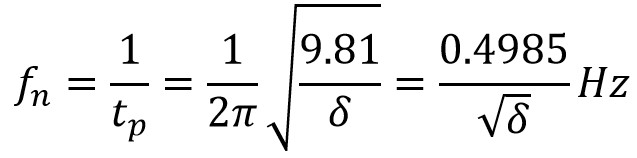
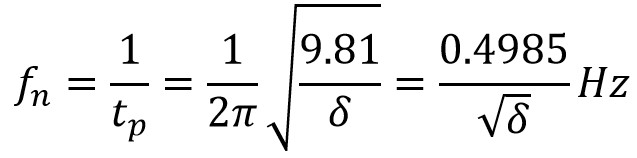
Where the δ is the static deflection (Extension or compression of the constraint)
Conclusion
We have derived the equation for finding the natural frequency of the Free Longitudinal Vibrations with three different methods, Equilibrium Method, Energy Method, Rayleigh’s method. If you have any further thoughts on this topic, let us know in the comment section below.

Leave a Reply