How to design Socket and Spigot Cotter Joint?

As you know, there are 3 different types of cotter joints. The first one is the Socket and Spigot cotter joint. The other two are the Sleeve and cotter joint, and Gib and cotter joint. In this article, we are going to discuss this first type of cotter joint construction and how to design this Socket and Spigot Cotter Joint to avoid possible failures in different parts of this cotter joint.

Cotter Joint

A Cotter joint is a joint which is locked by a cotter. A cotter is a flat wedge-shaped piece of rectangular cross-section and its width is tapered from one end to another for an easy adjustment. Mostly it is tapered on one side but sometimes it may be tapered on both sides.

• A Typical Cotter has a taper that varies from 1 in 48 to 1 in 24 and it may be increased up to 1 in 8, if a locking device is provided.
• In order to lock the cotter in place we need additional locking device such as a taper pin or a set screw on the lower end of the cotter to keep in its place.
• The cotter is usually made of mild steel or wrought iron.
• The cotter joint comes under the temporary fastening method.
• Cotter Joints are used to connect rigidly two co-axial rods or bars which are subjected to axial tensile or compressive forces.
• This cotter joints can be fount in well know applications such as in
  • Connecting a piston rod to the cross-head of a reciprocating steam engine,
  • Connecting a piston rod and its extension as a tail or pump rod,
  • in strap end of connecting rod

Socket and Spigot Cotter Joint

The following image represents the socket and spigot Cotter Joint.

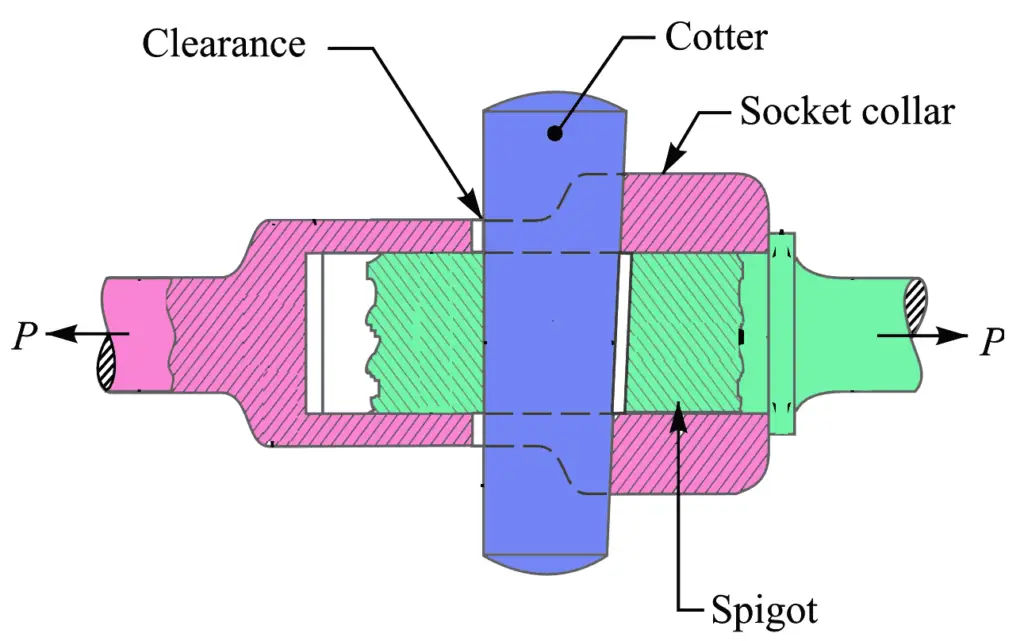
• In the above socket and spigot cotter joint, one end of the rods is provided with a socket type of end as shown as and the other end of the other rod is inserted into a socket.
• The end of the rod which goes into a socket is also called a spigot.
• A rectangular hole is made in the socket and spigot.
• A cotter is then driven tightly through a hole in order to make the temporary connection between the two rods.
• The load is usually acting axially, but it changes its direction, and hence the cotter joint must be designed to carry both the tensile and compressive loads.
• The compressive load is taken up by the collar on the spigot.

Design of Socket and Spigot Cotter Joint

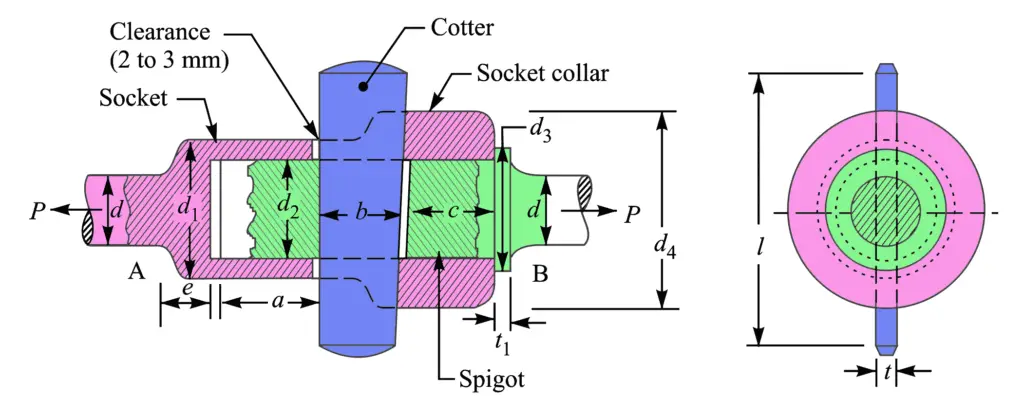
The socket and spigot cotter joint is shown in the above figure

Let us assume
P = Load carried by the rods,
d = Diameter of the rods,
d₁ = Outside diameter of socket,
d₂ = Diameter of the spigot or inside diameter of the socket,
d₃ = Outside diameter of spigot collar,
t₁ = Thickness of spigot collar,
d₄ = Diameter of socket collar,
c = Thickness of socket collar,
b = Mean width of cotter,
t = Thickness of cotter,
l = Length of cotter,
a = Distance from the end of the slot to the end of the rod,
σ_t = Permissible tensile stress for the material of the rod,
τ = Permissible shear stress for the cotter material, and
σ_c = Permissible crushing stress for the cotter material

All these above 14 assumed dimensions that involve in the design of socket and spigot cotter joint will be determined by considering all the possible modes of failure. Those are

• Failure of the rods in tension
• Failure of spigot in tension across the weakest section (or slot)
• Failure of the rod or cotter in crushing
• Failure of the socket in tension across the slot
• Failure of cotter in shear
• Failure of the socket collar in crushing
• Failure of socket end in shearing
• Failure of rod end in shear
• Failure of the spigot collar in Crushing
• Failure of the spigot collar in shearing
• Failure of cotter in bending

These possible failures of different parts of the socket and spigot cotter joint are considered to determine the above parameters.

1. Diameter of the Rods (d)

Considering the Failure of the rods in Tension we can determine the diameter of the rods.

In the above cotter joint, the rods may fail in tension due to the tensile load P.

We know that the cross-sectional Area resisting tearing inside the rod is given by

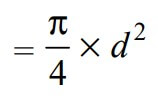
∴ The Tearing strength of the rods will be the product of the permissible tensile stress (σ_t) and the cross-sectional area that resist the tearing. We can write the relation as follows

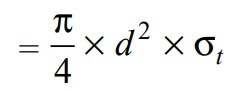
Now in order to resist the load, we must Equate this tearing strength to load (P), We can write

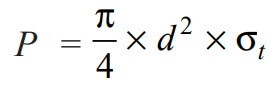
From this above relation, we can determine the required diameter of the rods (d).

2. Spigot Diameter or the Inside diameter of the Socket (d₂)

By considering the Failure of Spigot in Tension Across The Weakest Section, we can determine the Spigot Diameter or the Inside diameter of the Socket.

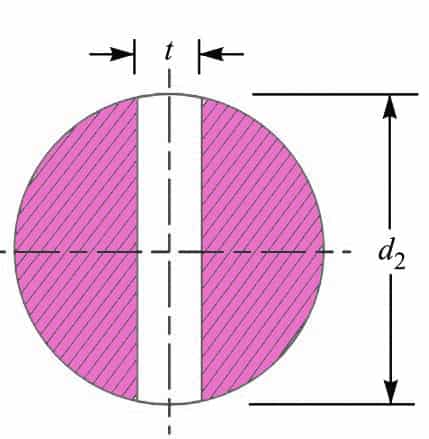
We have the weakest section in the spigot, which is the section where we have a slot for the cotter.

Therefore there is a chance that likely it will fail due to the tension.

The cross-sectional Area resisting tearing of the spigot across the slot can be written as

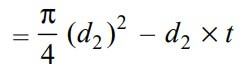
and tearing strength of the spigot across the slot will be the product of the permissible tensile stress (σ_t) and the cross-sectional area that resists this stress. We can write the relation as follows

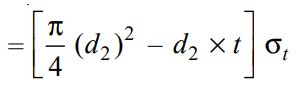
Now in order to resist the load, we must be Equating this tearing strength to load (P), We can write

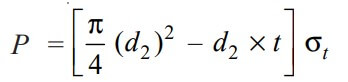
From this equation, the diameter of the spigot or inside diameter of the socket (d₂) will be determined.

In actual practice, the thickness of the cotter is usually taken as a quarter of the spigot diameter. which is d₂/4.

3. Induced crushing stress (σ_c) for Cotter

By considering the Failure of the rod or cotter in crushing we can determine the permissible crushing stress for the rod and cotter.

We know that the area that resists crushing of a rod or cotter

= d₂ × t

∴ The Crushing strength will be the product of the area that resists the crushing and the permissible crushing stress.

We can write the relation as = d₂ × t × σ_c

In order to resist the load, we must equate this crushing strength to the applied load (P), we can write have

P = d₂ × t × σ_c

From this relation, the induced crushing stress can be determined.

4. Outside Diameter of the Socket (d₁)

By considering the Failure of the socket in tension across the slot, we can determine the Outside Diameter of the Socket

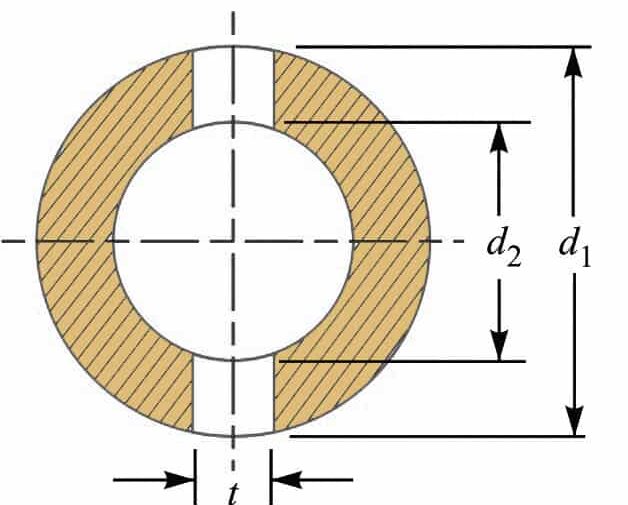
In the socket where we have the slot for the cotter, there is a possibility of failure. So we have to take this into the consideration while designing the socket for the cotter joint.

We know that the resisting cross-sectional area of the socket across the slot is shown in the above figure.

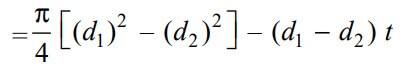
∴ The Tearing strength of the socket across the slot is will be the product of the permissible tensile stress (σ_t) in the and the cross-sectional area of the socket across the slot. We can write the relation as follows

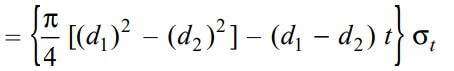
Now in order to resist the load, we must Equate this tearing strength to load (P), We can write

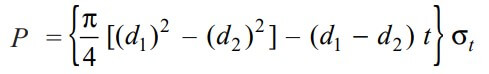
From this relation, we can determine the outside diameter of the socket (d₁).

5. Width Of Cotter (b)

The most important part of the Cotter’s joint is the cotter. We need to prevent any chance of failure in the cotter.

By considering the Failure of the cotter in shear, we can determine the width of the cotter.

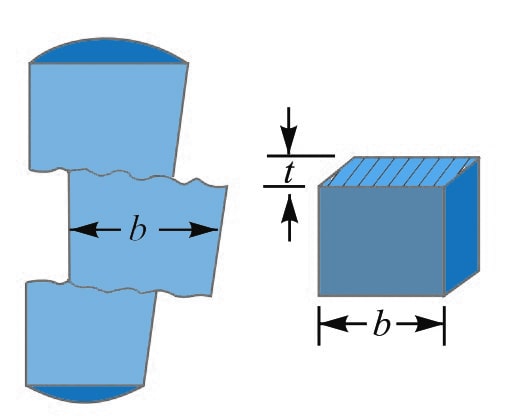
As you can see the above schematic representation of the Cotter being pulled away by the two equal opposite loads results in double shear.

The shearing area of the cotter will

= 2 b × t

and shearing strength of the cotter will be the product of the permissible shear stress of the

= 2 b × t × τ

Now equate this relation to the load (P), we can write as

P = 2 b × t × τ

From this relation, we can determine the width of cotter (b).

6. Diameter Of The Socket Collar (d₄)

By considering the Failure of the socket collar in crushing we can determine the diameter of the socket collar.

As the cotter slot is also extruded in the collar of the socket as we can see from the cotter joint cross-sectional view from the above.

We need to consider the possibility of failure of socket collar in crushing as shown below.

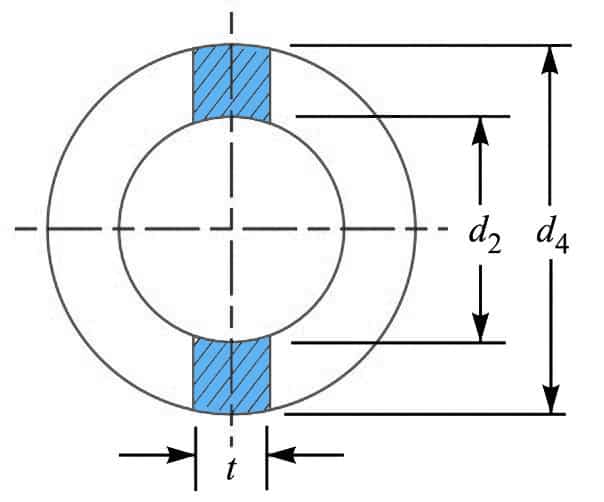
We know that area that resists crushing of socket collar

= (d₄ – d₂) t

and crushing strength will be the product of this area and the tensile stress.

We can write this relation=(d₄ – d₂) t × σ_c

Let us equate this with the load (P), we can write

P = (d₄ – d₂) t × σ

From this equation, we can determine the diameter of the socket collar (d₄).

7. Thickness Of Socket Collar (c)

We have considered the tensile stress and crushing in the socket end. And there is a high chance that the Socket may fail due to the shear stress also.

So let us consider the Socket end is experiencing double shear.

Therefore, the area that resists shearing of socket collar will be

= 2 (d₄ – d₂) c

Also, the shearing strength of the socket collar will be the product of the area and the shear stress.

We can write this relation as =2 (d₄ – d₂) c × τ

We need to equate this shearing strength against the load applied (P), we can write as

P = 2 (d₄ – d₂) c × τ

From this relation, we can determine the thickness of the socket collar (c).

8. Distance from the end of the slot to the End of Rod (a)

By considering the Failure of the rod end in shear, we can determine the distance from the end of the slot to the end of the rod.

Since the rod end is in double shear, therefore the area resisting the shear of the rod end

= 2 a × d₂ 

and shear strength of the rod end will be equal to the product of the area resisting the shear and the permissible shear stress. We can write this as follows

= 2 a × d₂ × τ 

Now let us equate this relation to the load (P), we can write

P = 2 a × d₂ × τ

From this relation, we can determine the distance from the end of the slot to the end of the rod (a).

9. Diameter Of The Spigot Collar (d₃)

By considering the Failure of the spigot collar in crushing, we can determine the diameter of the spigot collar.

The failure of the spigot collar in crushing is shown in the below figure.

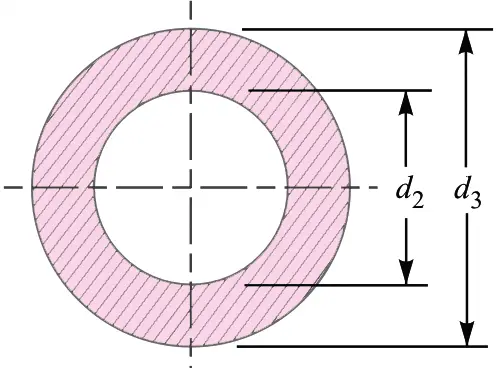
We know that area that resists the crushing of the collar

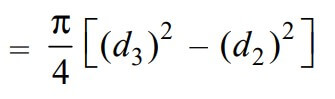
and the crushing strength of the collar will be the product of the area that resists the crushing of the collar and the permissible crushing stress.

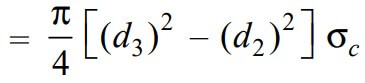
Let us equate this with the load (P), we can write

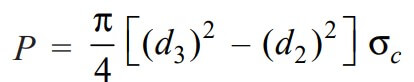
From this relation, we can determine the diameter of the spigot collar (d₃).

10. Thickness Of Spigot Collar (t₁)

By considering the Failure of the spigot collar in shearing, we can determine the thickness of the spigot collar.

The failure of the spigot collar in shearing is shown in the below schematic.

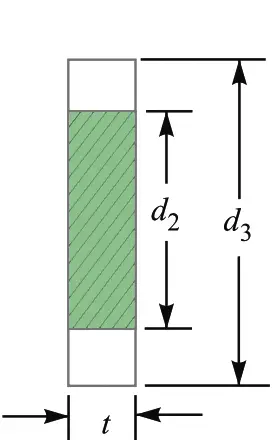
We know that area that resists shearing of the collar is

= π d₂ × t

and shearing strength of the collar can be written as the product of the permissible shearing stress and the area that resists the shearing.

We can write this relation as = π d₂ × t₁ × τ

Now let us equate this relation to the load (P), we can write it as

P = π d₂ × t1 × τ

From this relation, we can determine the thickness of the spigot collar (t₁).

11. Bending Stress in Cotter By considering the Failure of cotter under bending

We have been making assumptions in the above cases that the load is uniformly distributed over the various cross-sections of the joint. But in reality, this is very less likely to happen. The cotter joint is most likely subjected to bending.

In order to find out the bending stress induced in the cotter, it is assumed that the load on the cotter in the rod end is uniformly distributed while in the socket end it varies from zero at the outer diameter (d₄) and maximum at the inner diameter (d₂).

This has been illustrated in the following schematic diagram.

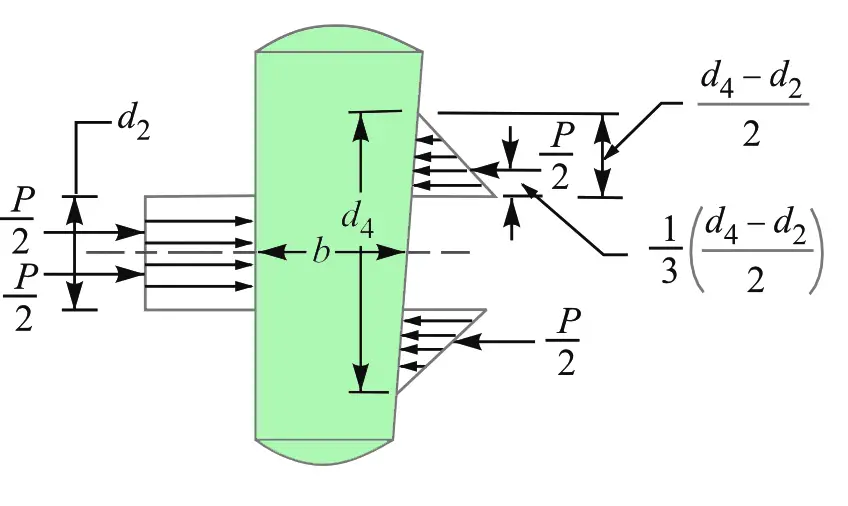
The maximum bending moment occurs at the center of the cotter and is given by

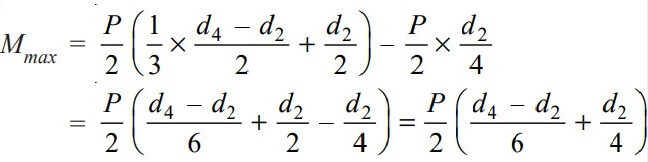
We know that section modulus of the cotter,

Z = t × b² / 6

∴ The Bending stress induced in the cotter

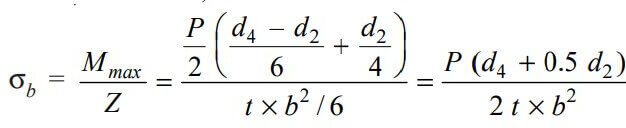
This bending stress induced in the cotter should be less than the allowable bending stress of the cotter.

12. Length of The cotter

As a standard, the length of cotter (l) is taken as 4 d.

13. Cotter Taper

The taper in the cotter should not exceed 1 in 24. In case a greater taper is required, then a locking device must be provided.

14.The draw of cotter

This is also as standard is taken as 2 to 3 mm.

Standard parameter for designing the Cotter Joint for steel material

When all the parts of the joint are made of steel, the following proportions in terms of diameter of the rod (d) are generally adopted :

d₁ = 1.75 d
d₂ = 1.21 d
d₃ = 1.5 d
d₄ = 2.4 d
a = c = 0.75 d
b = 1.3 d
l = 4 d
t = 0.31 d
t₁ = 0.45 d
e = 1.2 d
Taper of cotter = 1 in 25
The draw of cotter = 2 to 3 mm

If the rod and cotter are made of steel or wrought iron, then τ = 0.8 σ_t and σ_c= 2 σ_t may be taken.

Let us solve a sample problem to design a Socket and Spigot Cotter Joint.

Example Problem Statement

Design and draw a cotter joint to support a load varying from 30 kN in compression to 30 kN in tension. The material used is carbon steel for which the following allowable stresses may be used. The load is applied statically. Tensile stress = compressive stress = 50 MPa ; shear stress = 35 MPa and crushing stress = 90 MPa.

Answer:

Given data:

Load P = 30 kN = 30 × 10³ N
Permissible tensile Stress σ_t = 50 MPa = 50 N/mm²
Permissible Shear Stress τ = 35 MPa = 35 N/mm²
Permissible Crushing Stress σ_c= 90 MPa = 90 N/mm²

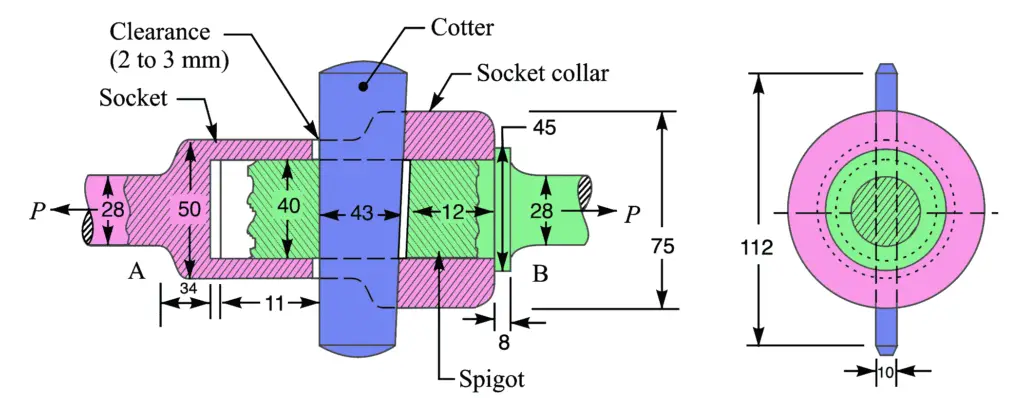
The Spigot and socket cotter joint as shown in below figure is designed as discussed below :

1. Diameter of the rods

Let d = Diameter of the rods.

Considering the failure of the rod in tension. We know that load (P),

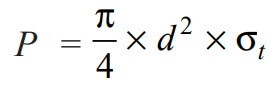
30 × 10³ = (π/4) × d² × 50
30 × 10³ = 39.3 d²
d² = 763
d = 27.6

We can assume the rod diameter d as 28mm.

2. Diameter of spigot and thickness of Cotter

Let d₂ = Diameter of the spigot or inside diameter of the socket, and t = Thickness of cotter.

As we have mentioned above the thickness of the cotter may be taken as d₂ / 4.

Considering the failure of the spigot in tension across the weakest section. We know that load (P),

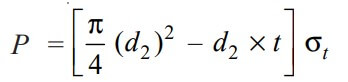
30 × 10³ = [(π/4) × (d₂)² – d₂ × (d₂ / 4)] × 50
30 × 10³ = 26.8 × (d₂)²
(d₂)² = 1119.4
d₂ = 33.4

The Diameter of spigot or inside diameter of socket (d₂) is 34mm and thickness of cotter (t) is = 34/4 = 8.5mm

Let us now check the induced crushing stress. We know that load (P),

30 × 10³ = d₂ × t × σ_c
30 × 10³ = 34 × 8.5 × σ_c
30 × 10³ = 289 σ_c
σ_c = 30 × 10³ / 289
σ_c = 103.8 N/mm²

This value of crushing stress σ_c is more than the given value of σ_c = 90 N/mm², therefore the dimensions d²
= 34 mm and t = 8.5 mm are not safe.

Now let us find the values of d₂ and t by substituting the value of σ_c= 90 N/mm² in the above expression, i.e.

30 × 10³ = d₂ × (d₂/4) × 90
30 × 10³ = 22.5 (d₂)²
(d₂) ² = 30 × 10³ / 22.5
(d₂) ² = 1333
d₂ = 36.5

The Diameter of the spigot or inside diameter of the socket (d2) is 36.5mm let us take 40mm to be on the safe side and the thickness of the cotter (t) will be = 40/4 = 10mm

3. Outside diameter of socket

Let d₁ = Outside diameter of socket.

Considering the failure of the socket in tension across the slot. We know that load (P),

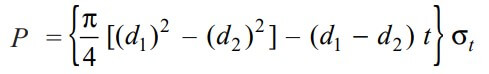
30 × 10³ = {(π/4) × [(d₁)² -(40)²]- (d₁-40) × (10)} × 50
30 × 10³/50 = 0.7854 (d₁)² – 1256.6 – 10 d₁ +400
(d₁)² – 12.7 d₁ – 1854.6 = 0

Solving this second-order algebraic equation we get d1 = 49.9. let us say the Outside diameter of the socket is 50mm.

4. Width of cotter

Let b = Width of cotter.

Considering the failure of the cotter in shear. Since the cotter is in double shear, therefore load (P),

P = 2 b × t × τ

30 × 10³ = 2 b × t × τ
30 × 10³ = 2 b × 10 × 35
30 × 10³ = 700 b
b = 30 × 10³ / 700
b = 43

The width of the cotter is 43mm.

5. Diameter of socket collar

Let d₄ = Diameter of socket collar.

Considering the failure of the socket collar and cotter in crushing. We know that load (P),

P = (d₄ – d₂) t × σ_c
30 × 10³ = (d₄ – d₂) t × σ_c
30 × 10³ = (d₄ – 40)10 × 90
30 × 10³ = (d₄ – 40) 900
d₄ – 40 = 30 × 10³ / 900
d₄ – 40 = 33.3
d₄ = 33.3 + 40
d₄ = 73.3

The diameter of the Socket Collar is 73.3mm, let us take 75mm.

6. Thickness of socket collar

Let c = Thickness of socket collar.

Considering the failure of the socket end in shearing. Since the socket end is in double shear, therefore load (P),

P = 2 (d₄ – d₂) c × τ

30 × 10³ = 2 (d₄ – d₂) c × τ
30 × 10³ = 2 (75 – 40 ) c × 35
30 × 10³ = 2450 c
c = 30 × 10³ / 2450
c = 12

Thickness of the collar is 12mm.

7. Distance from the end of the slot to the end of the rod

Let a = Distance from the end of slot to the end of the rod.

Considering the failure of the rod end in shear. Since the rod end is in double shear, therefore load (P),

P = 2 a × d₂ × τ

30 × 10³ = 2 a × d₂ × τ
30 × 10³ = 2a × 40 × 35
30 × 10³ = 2800 a
a = 30 × 10³ / 2800
a = 10.7

The Distance from the end of the slot to the end of the rod is 10.7mm, let us take 11mm.

8. Diameter of spigot collar

Let d₃ = Diameter of spigot collar.

Considering the failure of spigot collar in crushing. We know that load (P),

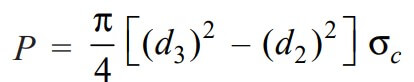
30 × 10³ = (π/4) × [(d₃)² – 40²] × 90
(d₃)² = 424 + (40)²
(d₃)² = 2024
d₃ = 45

The diameter of the spigot collar is 45mm.

9. Thickness of spigot collar

Let t₁ = Thickness of spigot collar.
Considering the failure of spigot collar in shearing. We know that load (P),

P = π d₂ × t₁ × τ
30 × 10³ = π d₂ × t₁ × τ
30 × 10³ = π × 40 × t₁ × 35
30 × 10³ = 4400 t₁
t₁ = 30 × 10³ / 4400
t₁ = 6.8

The thickness of the spigot collar is 6.8mm, let us take 8mm.

10. Length of Cotter

The length of cotter ( l ) is taken as 4 d.

l = 4 d = 4 × 28 = 112 mm

The dimension e is taken as 1.2 d.

e = 1.2 × 28 = 33.6 say 34 mm Ans.

Following is the Drawing with the parameter for the above-given problem. This is how we can calculate the spigot and socket cotter joint.

Applications of Cotter Joints

• Historically, the Cottar joint has been used to connect connecting rods to steam engines and pumps used in dumping mines.
• Cotter Joints are used between the piston rod and the tail of the pump rod.
• Cotter’s joints are used between the slide spindle and the fork of the valve mechanism.
• Cotter and Dowell arrange to join two parts of a flywheel.
• Foundation bolt: mainly used for fastening foundation and construction heavy machines
• In an automobile engine, the cotter joint is used to connect the extension of the piston rod with the connecting rod in the crosshead.
• The Cottar joint has historically been used to connect connecting rods to steam engines and pumps of dumping mines.
• It is used in bicycles to connect the paddle to the sprocket wheel.
• Use a wet air pump to join a tail rod with the piston rod.
• It is used to connects two rods of equal diameter subjected to axial forces.