How to calculate the Maximum Speed of a Reciprocating Pump?

The hydraulic machines, which convert the hydraulic energy into mechanical energy, are called turbines while the hydraulic machines which convert mechanical energy into hydraulic energy are called pumps. Hydraulic energy is in the form of pressure energy. If the mechanical energy is converted into pressure energy by means of centrifugal force acting on the fluid, the hydraulic machine is called a centrifugal pump. If the mechanical energy is converted into hydraulic energy (or pressure energy) by sucking the liquid into a cylinder in which a piston is reciprocating (moving backwards and forwards), which exerts the thrust on the liquid and increases its hydraulic energy (pressure energy), the pump is known as the reciprocating pump. In this article, let us understand how we can calculate the Maximum Speed of a Reciprocating Pump with an example problem.

Reciprocating Pump

The following schematic represents all the main parts of a reciprocating pump.

1. A cylinder with a piston, piston rod, connecting rod and a crank.
2. Suction pipe
3. Delivery pipe
4. Suction valve
5. Delivery valve

The above schematic diagram shows a single-acting reciprocating pump, consisting of a piston that moves forwards and backwards in a close-fitting cylinder. The movement of the piston is obtained by connecting the piston rod to the crank by means of a connecting rod. The crank is rotated by means of an electric motor.

Maximum Speed of a Reciprocating Pump

The Maximum speed of a reciprocating pump is determined by the fact that the pressure in the cylinder during suction and delivery stroke, should not fall below the vapour pressure of the liquid, flowing through the suction and delivery pipe. If the pressure in the cylinder is below the vapour pressure, the dissolved gases will be liberated from the liquid and cavitation will take place. Also, the continuous flow of liquid will not exist which means liquid separation will occur.

The pressure at which separation occurs is known as separation pressure and the head corresponding to separation pressure is called separation pressure head. It is denoted by h_sep.

For water, the limiting value of separation pressure head (h_sep) is 7.8 below atmospheric pressure head or 10.3 – 7.8 = 2.5 m abs. The separation may take place during the suction stroke or during the delivery stroke. The maximum speed of the reciprocating pump during suction and delivery strokes is calculated as:

(a) Maximum Speed during Suction Stroke

From the indicator diagram, drawn in the following, it is clear that the absolute pressure head during the suction stroke is minimum at the beginning of the stroke.

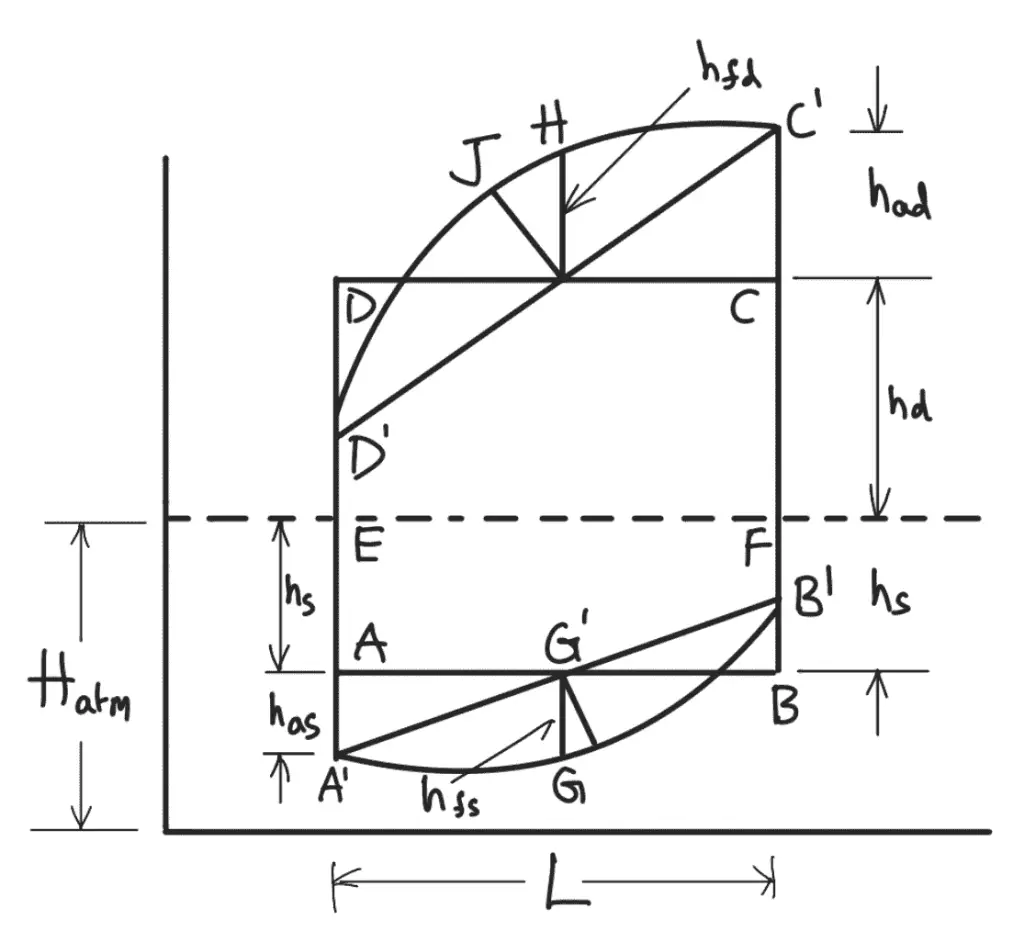
Thus, the separation can take place at the beginning of the stroke only. In that case, the abs. pressure head in the cylinder at the beginning of the stroke will be equal to the separation pressure head (h_sep).

h_sep = H_atm – h_s– h_as
h_as = H_atm – h_s– h_sep

Generally, the values of h_sep and h_s (suction head) are given and hence h_as the pressure head due to acceleration at the beginning of the suction stroke can be obtained. The value of h_as is also given by
equation as follows

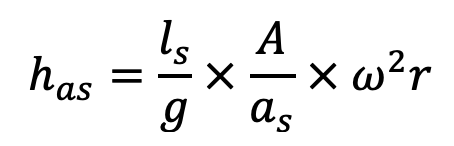
Equating the two values of has given by the above two equations

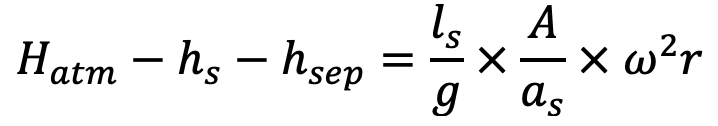
….. equation(a)

From the above equation(a), the value of the ω and hence speed N can be obtained. This speed is the maximum speed of the reciprocating pump without separation during the suction stroke.

(b) Maximum Speed during Delivery Stroke

During the delivery stroke, the probability of separation is only at the end of the delivery stroke. The pressure head in the cylinder at the end of the delivery stroke will be

= (H_atm + h_d) – h_ad m (abs.)

If separation is to be avoided, the above pressure head should be more than the separation pressure
head (h_sep). In the limiting case

h_sep = (H_atm + h_d) – h_ad
or
h_ad = (H_atm + h_d) – h_sep

But h_ad the pressure head due to acceleration at the end of the delivery stroke is also given by

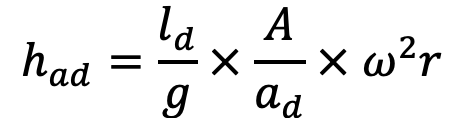
Equating the two values of h_ad we get

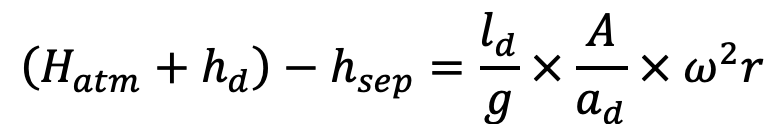
….. equation(b)

From the above equation(b), the value of ω and hence speeds N can be calculated. This is the maximum speed of the reciprocating pump without separation during the delivery stroke only.

The minimum of the two speeds given by the above two cases (a) and (b) is the maximum speed of the reciprocating pump without separation during suction and delivery strokes.

Let us solve an example problem to calculate the Maximum Speed of a Reciprocating Pump.

Calculating the Maximum Speed of a Reciprocating Pump

Problem Statement: Find the maximum speed of a single-acting reciprocating pump to avoid separation, which occurs at 3.0m of water (abs.) The pump has a cylinder of diameter 10cm and a stroke length of 20 cm. The pump draws water from a sump and delivers it to a tank. The water level in the sump is 3.5m below the pump axis and in the tank, the water level is 13m above the pump axis. The diameter and length of the suction pipe are 4cm and 5m while of the delivery pipe, the diameter and length are 3cm, and 20m respectively. Take atmospheric pressure head = 10.3m of water.

Answer:

Given data
Separation pressure head, h_sep = 3.0m of water (abs.)
Diameter of cylinder, D = 10cm = 0.10m
Stroke length L = 20 cm = 0.20 m
Crank radius, r = L /2 = 0.2/2 = 0.10m
Suction head, h_s = 3.5 m
Delivery head, h_d = 13m
Diameter of the suction pipe, d_s = 4cm = 0.04m
Length of the suction pipe, l_s = 5m
Diameter of delivery pipe, d_d = 3cm =0.03m
Length of delivery pipe, l_d = 20m
Atmospheric pressure head, H_atm= 10.3 m

(i) Maximum speed of the Reciprocating Pump during suction stroke without separation is obtained from the relation, given by equation (a)

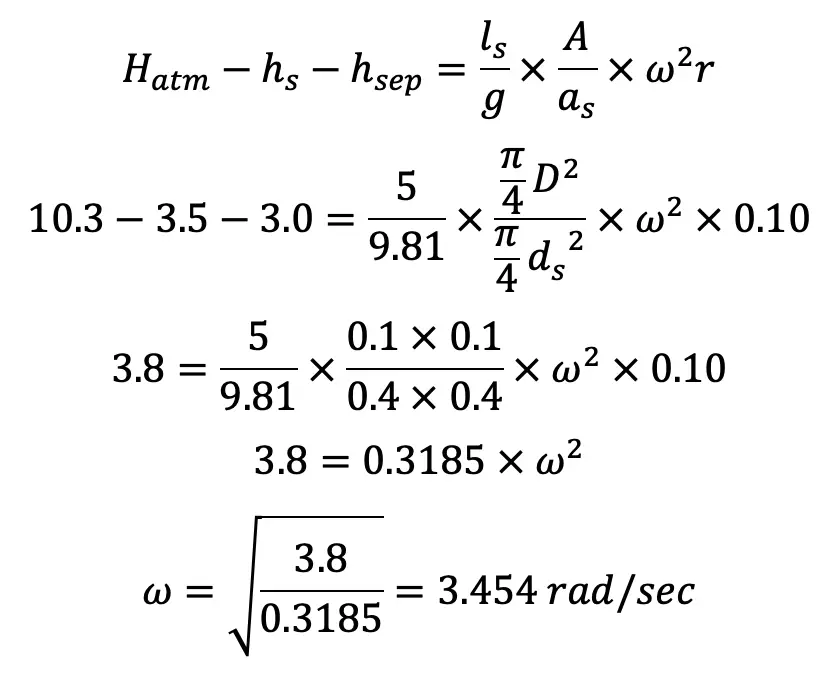
The angular velocity of a Reciprocating Pump is 3.454 rad/sec. From the angular velocity, we can calculate the speed as follows.

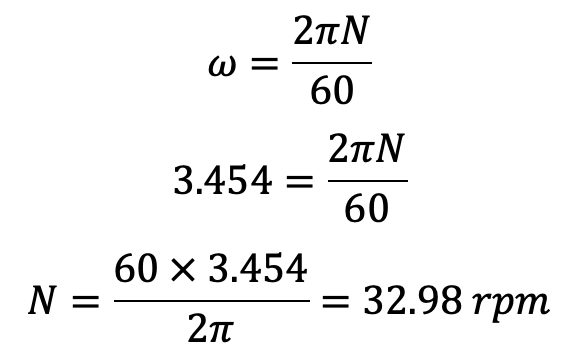
The Maximum speed of a Reciprocating Pump during suction stroke without separation is 32.98 rpm.

(ii) Maximum speed of the Reciprocating Pump during the delivery stroke without separation is obtained from equation (b),

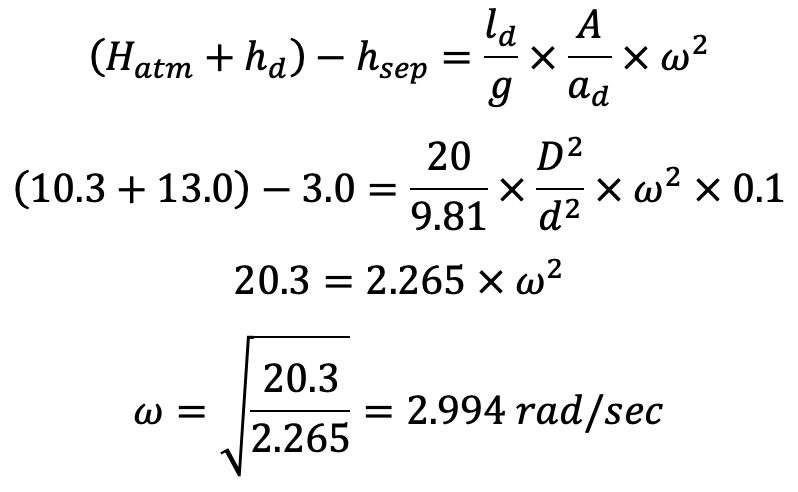
The angular velocity of a Reciprocating Pump is 2.994 rad/sec. From the angular velocity, we can calculate the speed as follows.

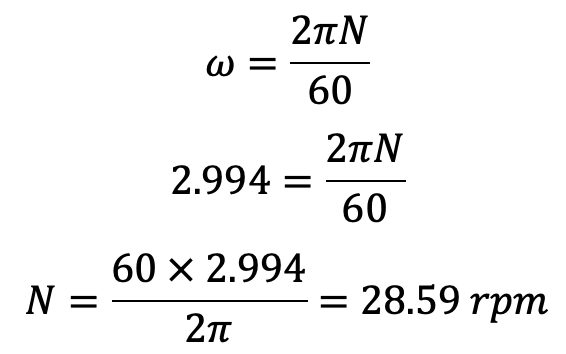
the Maximum speed of the Reciprocating Pump during the delivery stroke without separation is 28.59 rpm.

The minimum of the two speeds given by the above equations is the maximum speed of the pump, without separation.

The Maximum speed of the Reciprocating Pump without separation for the given problem statement is 28.59 RPM.

This is how we can calculate the Maximum Speed of a Reciprocating Pump from the given inputs. Let us know what you think about this article in the comment section below.