How to calculate the force required to lift the load with Pulley?

Lifting a load with a pulley seems simple and effortless but, have you ever wondered how much effort is required to lift a certain amount of load with a pulley or system of pulleys? Let us understand the different systems of pulley arrangments and see how we can calculate the force required to lift the load with a pulley.

Pulleys

A pulley is a wheel on an axle or shaft that is designed to support movement and change of direction of a taut cable or belt or transfer of power between the shaft and cable or belt.

Pulley Applications

We mostly see pulleys in sailing ships, cranes and conveyer belt systems. We have many applications in the following segments.

• Shipping and marine applications
• Industrial equipment
• Heavy machinery

A specialized block and tackle system are widely used for sailing vessels and fishing ships to allow operators to lift heavy loads with minimal force.

System of Pulleys

Mechanical Systems typically use multiple pulleys to increase mechanical advantage as it reduces the force needed to lift or pull the weight. However, the increased number of pulleys used decreases the efficiency of the system due to friction.

A systematic arrangement of one or more pulleys may provide a simple and convenient lifting machine. In its simplest form, it consists of only one pulley over which a rope or chain passes as shown in the below figure.

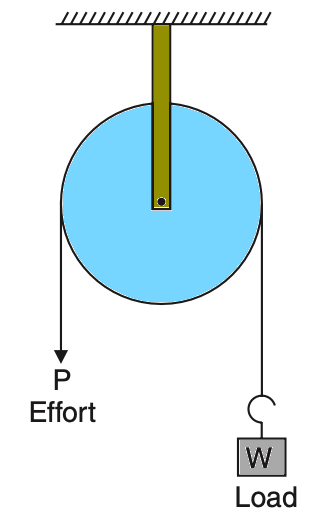
In this case, the velocity ratio is equal to one since the distance moved by effort is equal to the distance moved by the load. It just performs by changing the direction of the applied force. Depending on the arrangement, pulleys are classified as:

(1) First order pulley system
(2) Second order pulley system
(3) Third order pulley system

At times, it may be difficult or maybe detour to find the velocity ratio directly. In such cases, ideal conditions may be assumed (neglecting friction) and mechanical advantage may be found first with the leaver Arm. Then applying Velocity Ratio (VR) = Mechanical Advantage (MA) for the ideal machine, the velocity ratio is found.

Mechanical Advantage: This is the ratio of load lifted to effort applied. Thus, if W is the load and P is the corresponding effort, then

Mechanical Advantage = W / P

Velocity Ratio: This is the ratio of the distance moved by the effort to the distance moved by the load in the same interval of time. Thus,

Velocity Ratio = D / d

where,
D – distance moved by the effort
d – distance moved by the load

Mechanics of Solids

Load is the resistance to be overcome by the machine. the effort is the force required to overcome the resistance to get the work done by the machine.

This method of determining velocity ratio is used for various pulley systems considered here.

1. First Order Pulley System

A first-order pulley system is shown in the below figure.

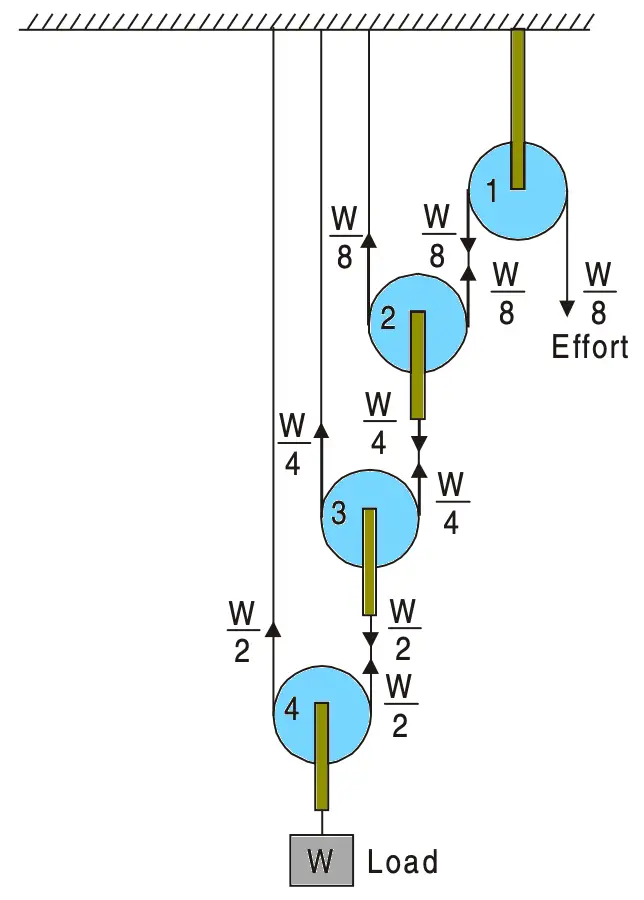
Pulley No. 1 is fixed in position to support at the top. A rope passes over this pulley and one end of this rope is tied to the support at the top, making a loop, in which pulley No. 2 is suspended and effort is applied at the other end. One end of another rope is tied to pulley No. 2 and the other end to the top support which makes a loop in which pulley No. 3 is suspended. Similarly, a number of pulleys can be arranged as shown, when an effort is applied to lift the load except for the first pulley all other pulleys move vertically. Therefore, the first pulley is termed a fixed pulley and the others as movable pulleys.

Let an effort P be applied to lift a load W.

In an ideal pulley system (friction = 0), the rope which passes over pulley No. 4 is subjected to a tension W/2.

Then tension in the rope that passes over pulley No. 3 is W/4 and tension in the rope that passes over pulley No. 2 is W/8.

Hence, an effort equal to W/ 8 is required to lift a load W.

P = W/8 and hence Mechanical Advantage (MA) = W/P = W/(W/8) = 8 = 2³

But in an ideal machine, Velocity Ratio (VR) = Mechanical Advantage (MA)

∴ VR = 2³

It is to be noted that in the system considered, there are three movable pulleys and the velocity ratio is 2³.

If there are only two movable pulleys, then the velocity ratio would be 4 which will be 2².

In general, in the first order pulley system, velocity ratio (VR) is given by 2ⁿ, where, n is the number of movable pulleys present in the system. Thus, in the first-order pulley system

Velocity Ratio (VR) = 2ⁿ

2. Second-Order Pulley System

The below figure shows a second-order pulley system.

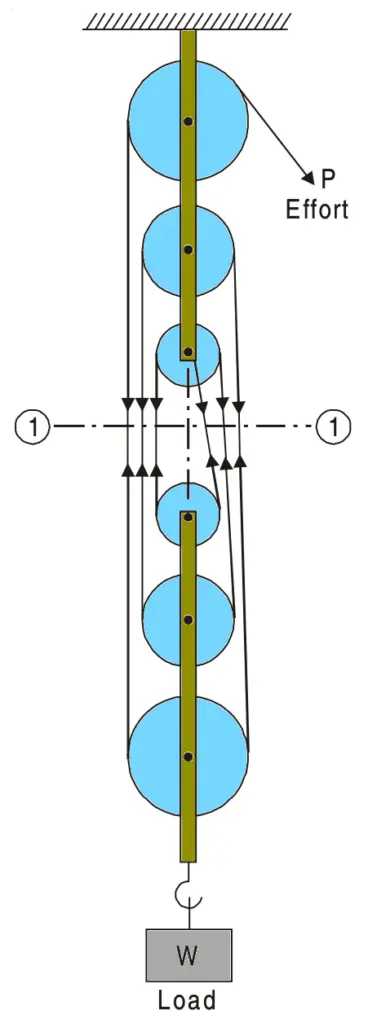
This system consists of a top pulley block and a bottom pulley block. In a pulley block, pulleys may be arranged side by side or maybe one below the other as shown in the above second-order pulley system.

The top pulley block is fixed in position to the top support whereas the bottom pulley block can move vertically along with the load which is attached to it. One end of the rope is attached to the hook provided at the bottom of the top pulley block and the effort is applied at the other end. A single rope goes round all the pulleys. Let an effort P be applied to lift a load W.

Neglecting frictional losses, the tension in the rope all along the length is P.

Take the section along (1)–(1) and consider the equilibrium of the bottom pulley block. The load W is lifted using six ropes having equal tension P

W = 6P
P = W/6

Mechanical Advantage (MA) = W/P = W/(W/6) = 6

But Velocity Ratio (VR) = Mechanical Advantage (MA) in ideal condition
VR = 6.

In general, in the second-order pulley system velocity ratio is equal to twice the number of movable pulleys in the system.

That is, VR = 2n
where n is the total number of movable pulleys in the system.

3. Third Order Pulley System

The arrangement of the pulleys in the third-order system is shown in the below figure.

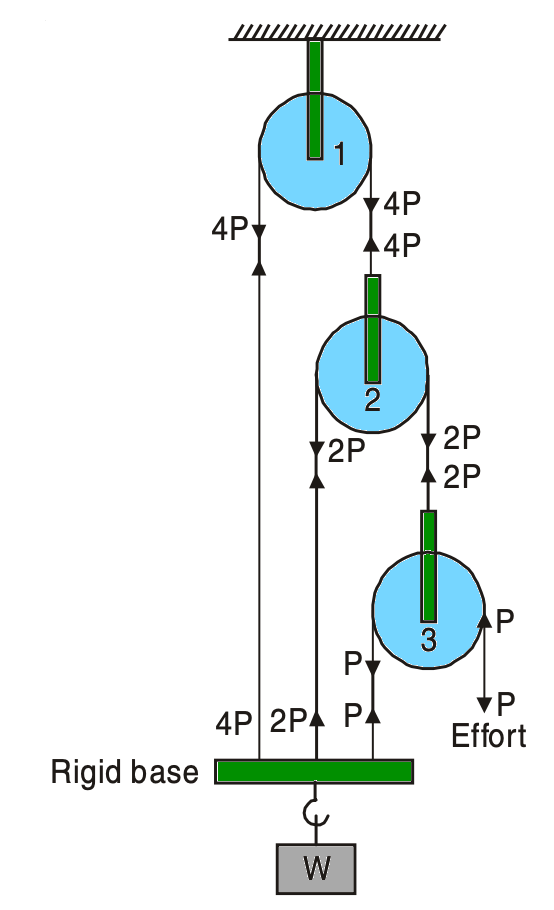
In this system, a pulley (No. 1) is fixed to the top support, over which a rope passes. One end of the rope is attached to a rigid base at the bottom. The other end is attached to a second pulley. Over this pulley another rope passes, whose one end is attached to the same rigid base and the other end to a third pulley as shown. Likewise, a series of pulleys can be arranged. The load to be lifted will be attached to the rigid base.

Referring to the above third-order pulley system, let the effort required to be P to lift a load W. Then neglecting friction,

Tension in the rope which passes over pulley No. 3 = P
Tension in the rope which passes over pulley No. 2 = 2P
Tension in the rope which passes over pulley No. 1 = 4P
∴ A total force of 7P is acting on the base.
∴ Lifting force produced on the base = 7P

Considering the equilibrium of rigid base, 7P = W

Mechanical Advantage (MA) = W/P = 7

But in an ideal machine, Velocity Ratio (VR) = Mechanical Advantage (MA), and hence VR = 7

It can be easily seen that if there are only two pulleys, VR = 3 and if there is only one pulley,
VR = 1.

Therefore, in general, for the third-order pulley system:
VR = 2ⁿ – 1
where n = number of pulleys.

Example Problems to finding the force required to lift the load with Pulley

Example problem 1: In the first-order system of pulleys, there are three movable pulleys. What is the effort required to raise a load of 6000 N ? Assume the efficiency of the system is 80%. If the same load is to be raised using 520 N, find the number of movable pulleys that are necessary.
Assume a reduction of efficiency of 5% for each additional pulley used in the system.

Answer:

Velocity Ratio (VR) = 2ⁿ,
where n is the number of movable pulleys.

VR = 2³ = 8

Now, Mechanical Advantage (MA) = η × VR = 0.8 × 8 = 6.4
We know Mechanical Advantage (MA) = W/P = 6.4
P = W/6.4
P = 6000/6.4
P = 937.5 N

In the second case,
Effort = 520 N
Efficiency η = 0.80 – n₁ × 0.05
where n₁ = number of additional pulleys required and equal to (n – 3).
Mechanical Advantage (MA) = η × VR
MA = W/P = η × VR
W = P × η × 2_n
W = P(0.8 – n₁ × 0.05) × 2ⁿ
W = P[0.8 – (n – 3) × 0.05] 2ⁿ

By going for a trial and error solution, starting with one additional pulley i.e., totally with four pulleys,
W = 520 [0.8 – (4 – 3) × 0.05] 2⁴ = 6240 N

if four pulleys are used, a load of 6240 N can be raised with the help of 520 N effort.

∴ Number of movable pulleys required = 4

Example Problem 2: What force is required to raise the load W shown in the below system of pulleys? Assume the efficiency of the system is 85%.

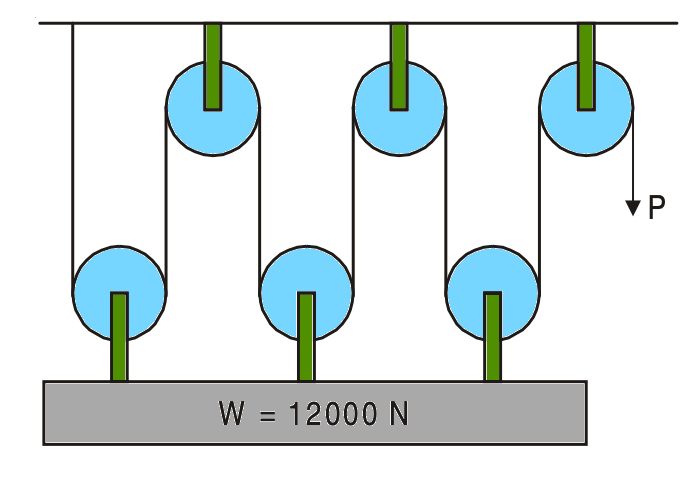
Answer:

The pulley system shown in the above pulley system is a variation of the second-order pulley system.

Velocity Ratio (VR) = 2 × number of movable pulleys = 6
Mechanical Advantage (MA) = η × VR
MA = 0.85 × 6
MA = 5.1
MA = W/P = 5.1
P = W/51
P = 12,000/5.1
P = 2352.94 N

The force (P) of 2352.94N is required to lift the load of 12000N.

Example Problem 3: Find the pull required to lift the load W shown in the below figure assuming the efficiency of the system to be 78%.

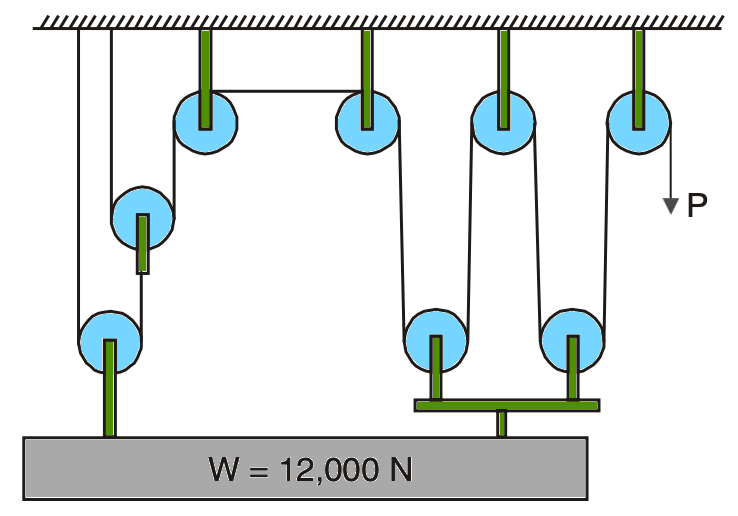
Answer:

The pulley system is shown in the above figure is a combination of a first-order system and a second-order system as shown in illustrated in the below figures (a) and (b).

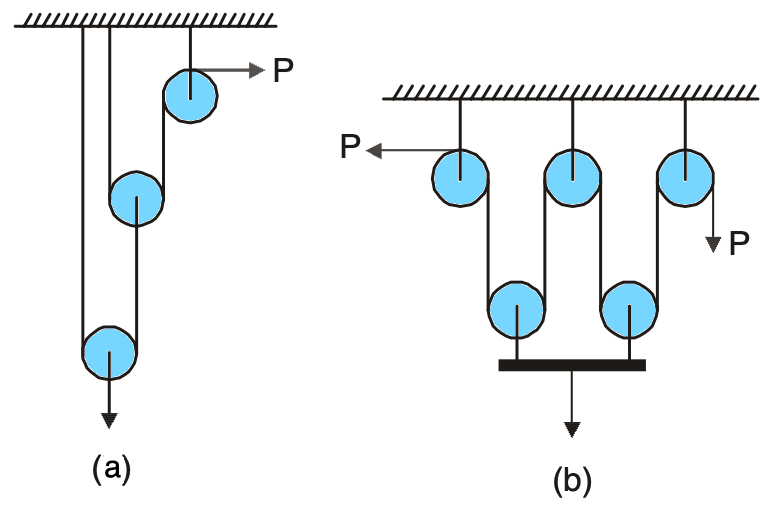
Let load W be lifted by a distance x.

Consider the first-order system portion as shown in figure (a). Here there are two movable pulleys.

Hence Velocity Ratio (VR) = 22 = 4

In this portion, P moves by 4x.

Now, consider the second-order pulley system portion as shown in figure (b). Here there are two movable pulleys.

Hence Velocity Ratio (VR) = 2 × 2 = 4.

The distance moved by the effort in this system = 4x.

Hence, the total distance moved by the effort in the given system = 4x + 4x = 8x

Velocity Ratio (VR) = 8x/x = 8

Now, Mechanical Advantage (MA) = η × VR
MA = 0.78 × 8
MA = 6.24
MA = W/P = 6.24
P = 12,000/6.24
P = 1923.08 N

The pulling load (P) of 1923.08 N is required to lift the load of 12000N.

Example Problem 4: A lifting machine consists of pulleys arranged in the third-order system. There are three pulleys in the system. A load of 1000 N is lifted by an effort of 180 N. Find the efficiency of the machine and the effort lost in friction.

Answer:

For the third-order system of pulleys,
Velocity Ratio (VR) = 2ⁿ – 1
where n is the number of pulleys in the system.
Velocity Ratio (VR) = 2³ – 1 = 7

Now, Mechanical Advantage (MA) = η × VR
MA = W/P = η × VR
η = (W/P) × (1/VR)
η = (1000/180) × (1/7)
η = 0.7937 = 79.37%

Now,the Ideal effort,
VR = W/P_i
P_i = W/VR
P_i = 1000/7
P_i = 142.86 N

The Effort lost in friction = P – P_i
= 180 – 142.86
= 37.14 N

the Effort lost in friction is 37.14 N

Example problem 5: What force P is required to raise a load of 2500 N in the system of pulleys shown in the below figure. Assume the efficiency of the system is equal to 70%.

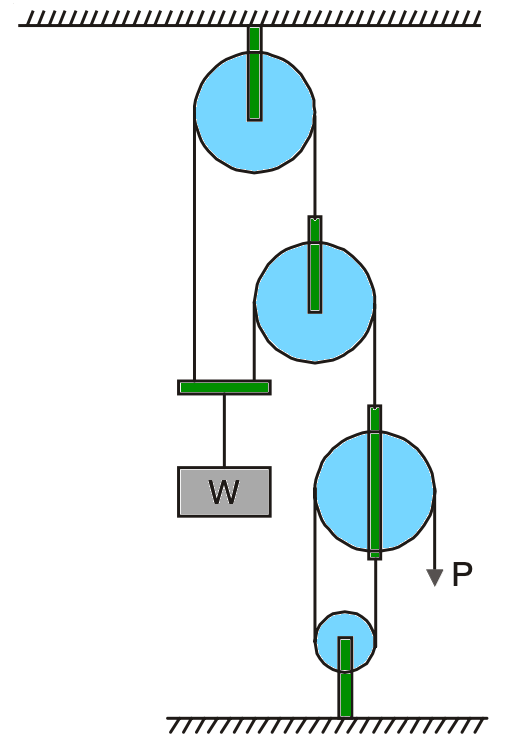
Answer:

The Figure can be split into two simple systems as shown in the below figures (a) and (b).

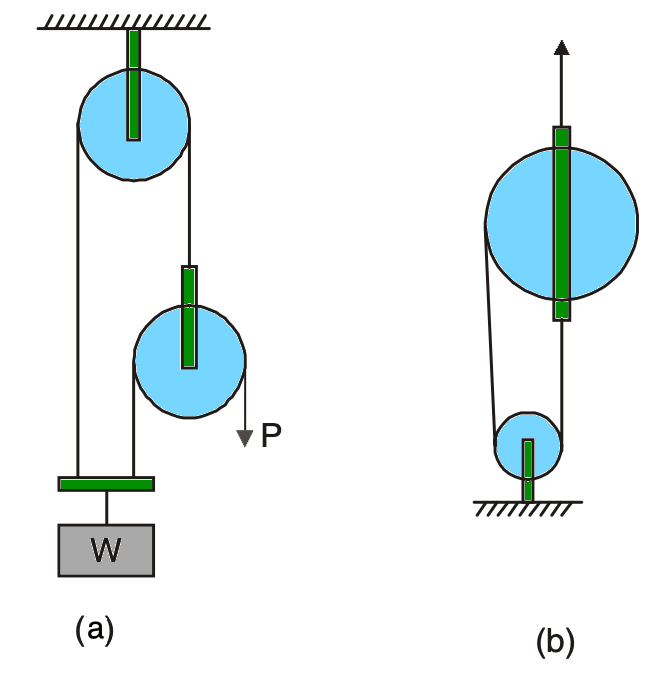
What is shown in figure (a) is a third-order pulley system having two pulleys.
Velocity Ratio (VR) = 2ⁿ – 1
VR = 2² – 1 = 3

Figure (b) is also a third-order system, having two pulleys.

Velocity Ratio (VR) = 2² – 1 = 3

The Velocity Ratio (VR) of the whole system will be = 3 + 3 = 6

Now, Mechanical Advantage (MA) = η × VR
MA = W/P = η × VR
P = W/η × VR
P = 2500/0.7 × 6
P = 595.24 N

A force of 595.24N is required to raise a load of 2500 N in the system of pulleys as shown above.

Conclusion

We have discussed the pulley and some of the application of the pulley in the different industries. Also breifly explained the 3 systematic arrangements of pulleys and explained how to calcuate the force or effort required to lift load with pulley or system of pulleys. Also solved 5 Example Problems to find the force required to lift the load with Pulley. Let us know what do you think about this article in the comment section below.