How to calculate Stress in Leaf Springs?

A spring is defined as an elastic body, whose function is to distort when loaded and to recover its original shape when the load is removed. It absorbs or controls energy due to either shock or vibration so it can be used as shock absorbers and vibration dampers. It is also used to apply forces, as in brakes, clutches, and spring-loaded valves. We have already discussed different types of springs and also about the leaf springs in detail. Let us discuss the stress in Leaf Springs.

Applications of Springs

The various important applications of springs are as follows:

1. To cushion, absorb, or control energy due to either shock or vibration as in car springs, railway buffers, aircraft landing gears, shock absorbers, and vibration dampers.
2. To apply forces, as in brakes, clutches, and spring-loaded valves.
3. To control motion by maintaining contact between two elements as in cams and followers.
4. To measure forces, as in spring balances and engine indicators.
5. To store energy, as in watches, toys, etc.

Types of Springs

Though there are many types of springs, the following, according to their shape, are important from the subject point of view.

• Helical springs
• Conical and volute springs
• Torsion springs
• Laminated or Leaf springs
• Disc or Belleville springs
• Special-purpose springs

We have discussed more details for the other springs in a separate article here! Also we discussed the Leaf springs in detailed manner in the previous article.

Leaf Spring

The laminated or leaf spring (also known as flat spring or carriage spring) consists of a number of flat plates (known as leaves) of varying lengths held together by means of clamps and bolts. These are mostly used in automobiles. The advantage of leaf spring over helical spring is that the ends of the spring may be guided along a definite path as it deflects to act as a structural member in addition to energy absorbing device. Thus the leaf springs may carry lateral loads, brake torque, driving torque etc., in addition to shocks.

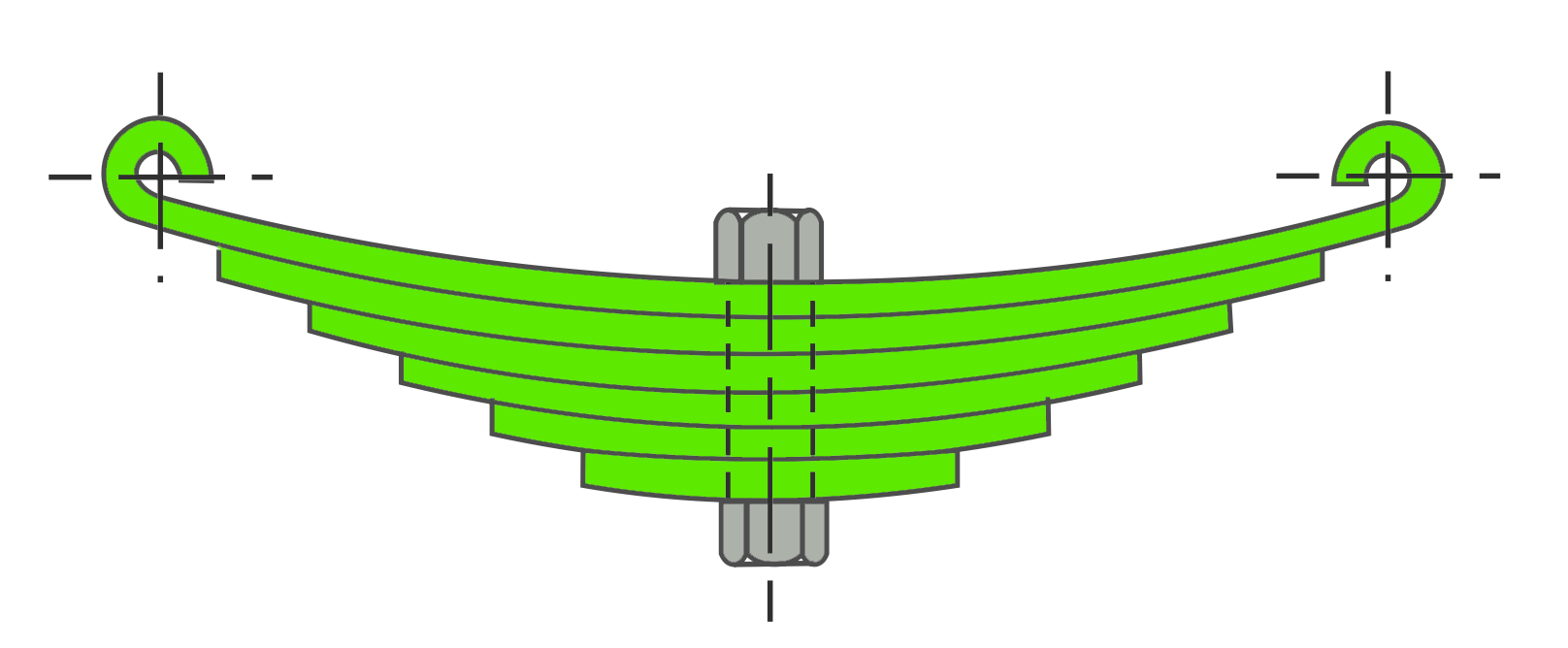
Stress in Leaf Springs

We have already discussed that the stress in the full length leaves is 50% greater than the stress in the graduated leaves in the previous article. In order to utilise the material to the best advantage, all the leaves should be equally stressed.

This condition may be obtained in the following two ways:

1. By making the full length leaves of smaller thickness than the graduated leaves. In this way, the full length leaves will induce smaller bending stress due to small distance from the neutral axis to the edge of the leaf.
2. By giving a greater radius of curvature to the full length leaves than graduated leaves, as shown in the following figure, before the leaves are assembled to form a spring. By doing so, a gap or clearance will be left between the leaves. This initial gap, as shown by C in the following figure, is called nip. When the central bolt, holding the various leaves together, is tightened, the full length leaf will bend back as shown dotted in the following figure and have an initial stress in a direction opposite to that of the normal load.

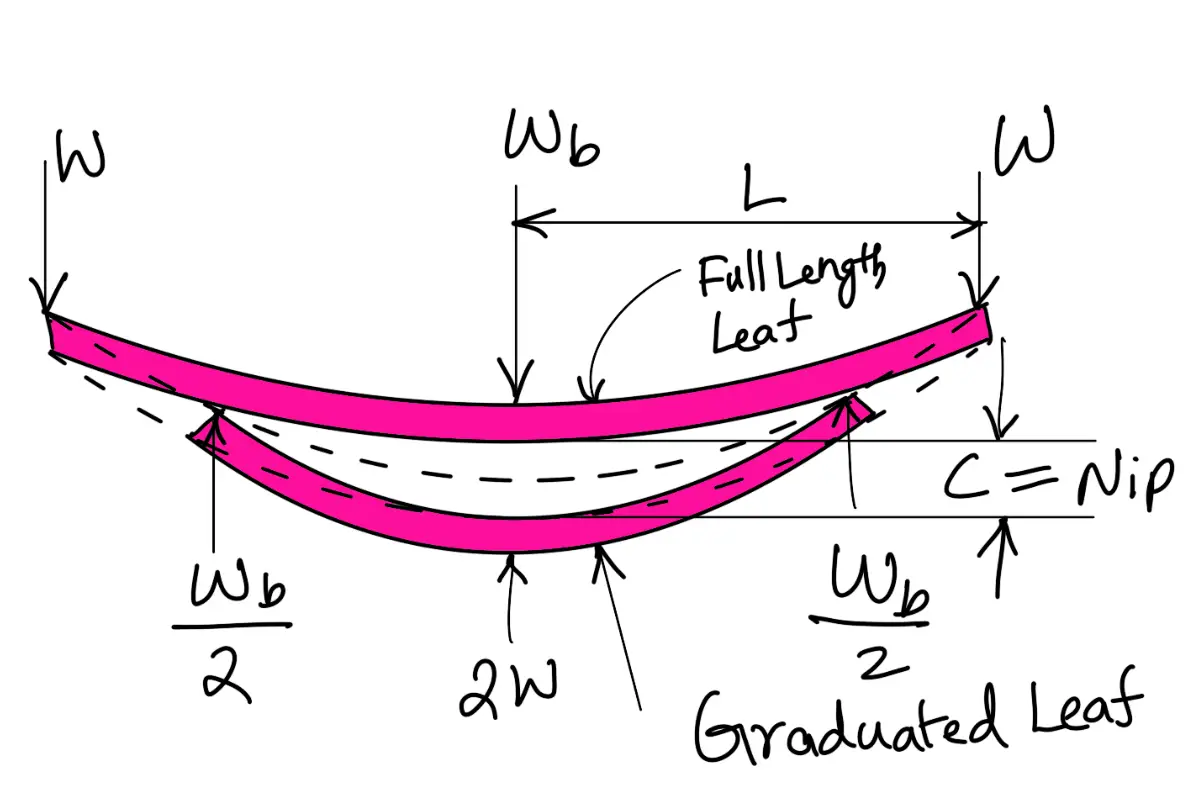
The graduated leaves will have an initial stress in the same direction as that of the normal load. When the load is gradually applied to the spring, the full length leaf is first relieved of this initial stress and then stressed in opposite direction. Consequently, the full length leaf will be stressed less than the graduated leaf. The initial gap between the leaves may be adjusted so that under maximum load condition the stress in all the leaves is equal, or if desired, the full length leaves may have the lower stress. This is desirable in automobile springs in which full length leaves are designed for lower stress because the full length leaves carry additional loads caused by the swaying of the car, twisting and in some cases due to driving the car through the rear springs. Let us now find the value of initial gap or nip C.

Consider that under maximum load conditions, the stress in all the leaves is equal. Then at maximum load, the total deflection of the graduated leaves will exceed the deflection of the full length leaves by an amount equal to the initial gap C. In other words,

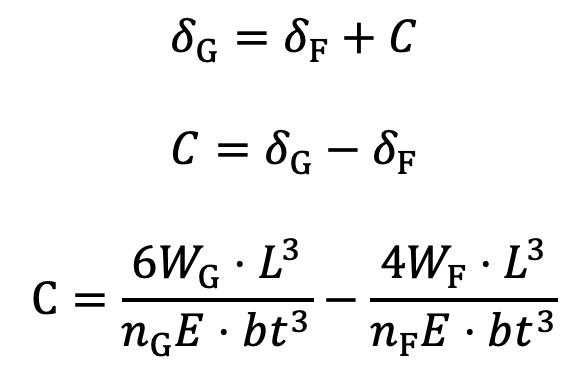
Since the stresses are equal, therefore

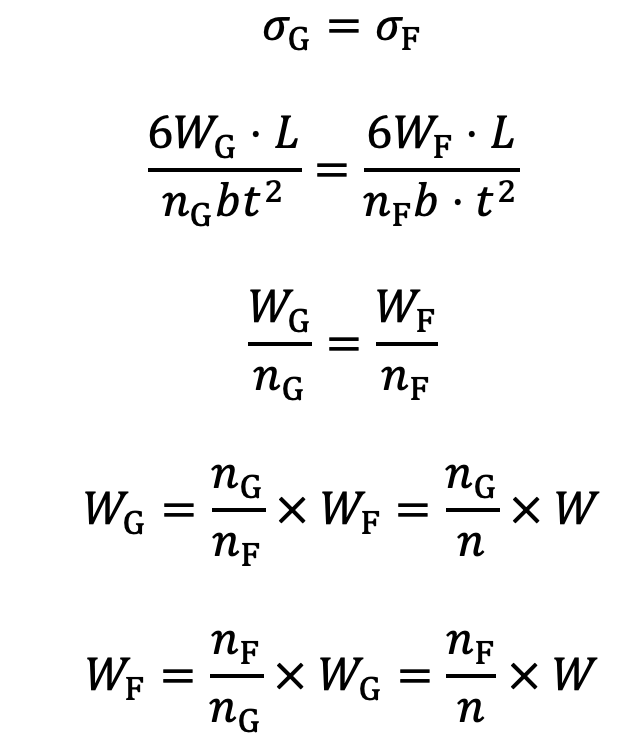
Substituting the values of W_G and W_F in the above equation, we get

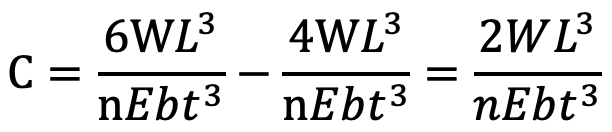
The load on the clip bolts (W_b) required to close the gap is determined by the fact that the gap is equal to the initial deflections of full length and graduated leaves.

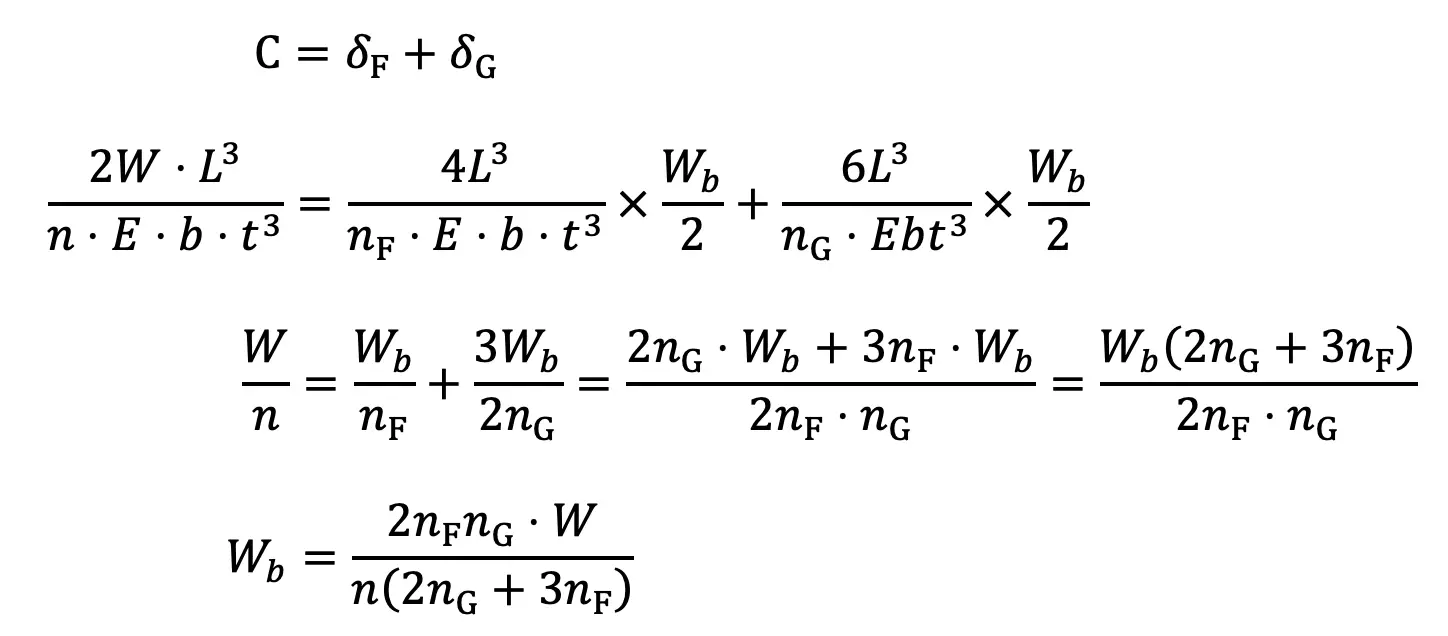
The final Stress in Leaf Springs Leaves will be the stress in the full length leaves due to the applied load minus the initial stress.

∴ Final Stress in Leaf Springs Leaves

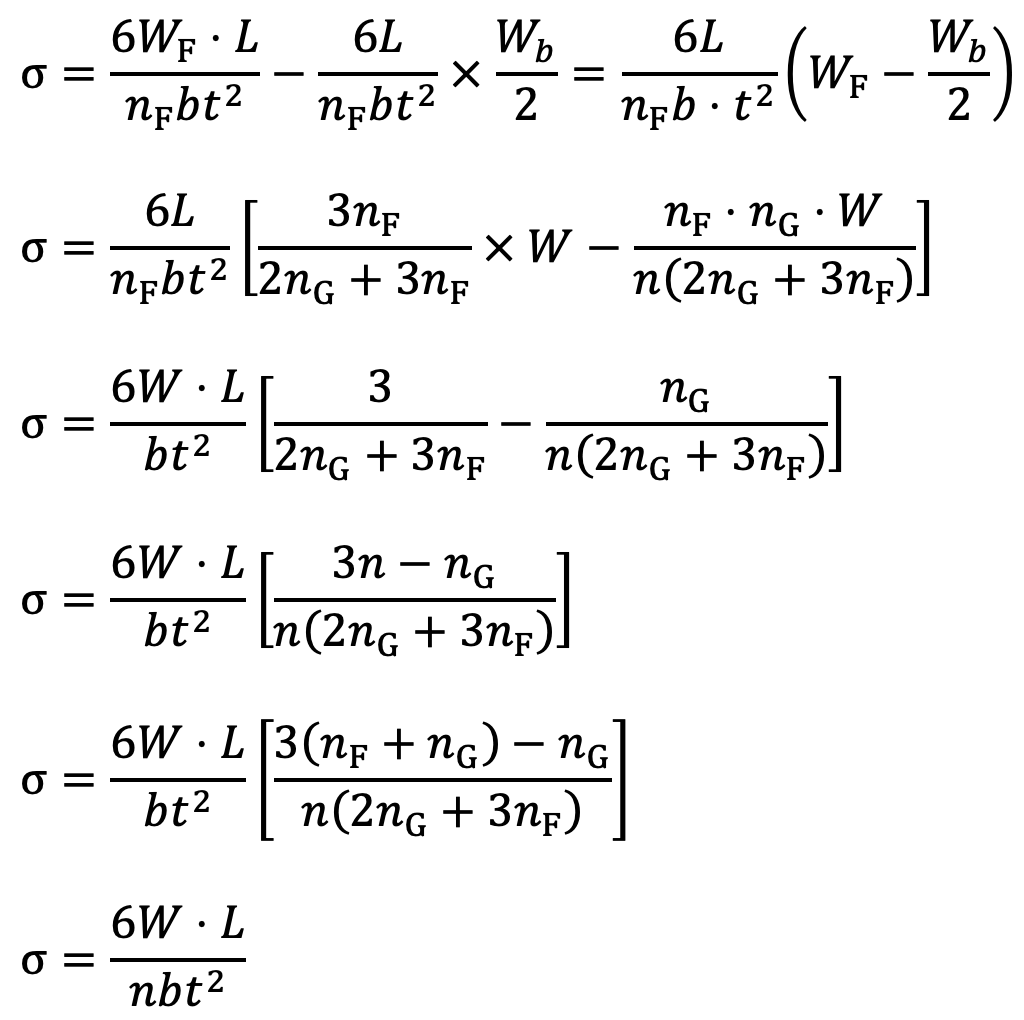
Notes :

1. The final stress in the leaves is also equal to the stress in graduated leaves due to the applied load plus the initial stress.
2. The deflection in the spring due to the applied load is same as without initial stress.