Sometimes it is necessary to refer to specific lattice planes of atoms within a crystal structure, or it may be of interest to know the crystallographic orientation of a plane or group of planes in a crystal lattice. To identify crystal planes in cubic crystal structures or hexagonal structures, the Miller notation system is used. Let us see how we can calculate Miller Indices for Crystallographic planes in the Cubic system and Hexagonal Crystal Structure.

Miller Indices for Crystallographic planes
The Miller indices of a crystal plane are defined as the reciprocals of the fractional intercepts (with fractions cleared) that the plane makes with the crystallographic x, y, and z axes of the three nonparallel edges of the cubic unit cell.
The cube edges of the unit cell represent unit lengths, and the intercepts of the lattice planes are measured in terms of these unit lengths.
Procedure for Determining Miller Indices for Cubic Crystal plane
The procedure for determining the Miller indices for a cubic crystal plane is as follows:
- Choose a plane that does not pass through the origin at (0, 0, 0).
- Determine the intercepts of the plane in terms of the crystallographic x, y, and z axes for a unit cube. These intercepts may be fractions.
- Form the reciprocals of these intercepts.
- Clear fractions and determine the smallest set of whole numbers that are in the same ratio as the intercepts. These whole numbers are the Miller indices of the crystallographic plane and are enclosed in parentheses without the use of commas. The notation (hkl) is used to indicate Miller indices in a general sense, where h, k, and l are the Miller indices of a cubic crystal plane for the x, y, and z axes, respectively.
The following figure shows three of the most important crystallographic planes of cubic crystal structures.
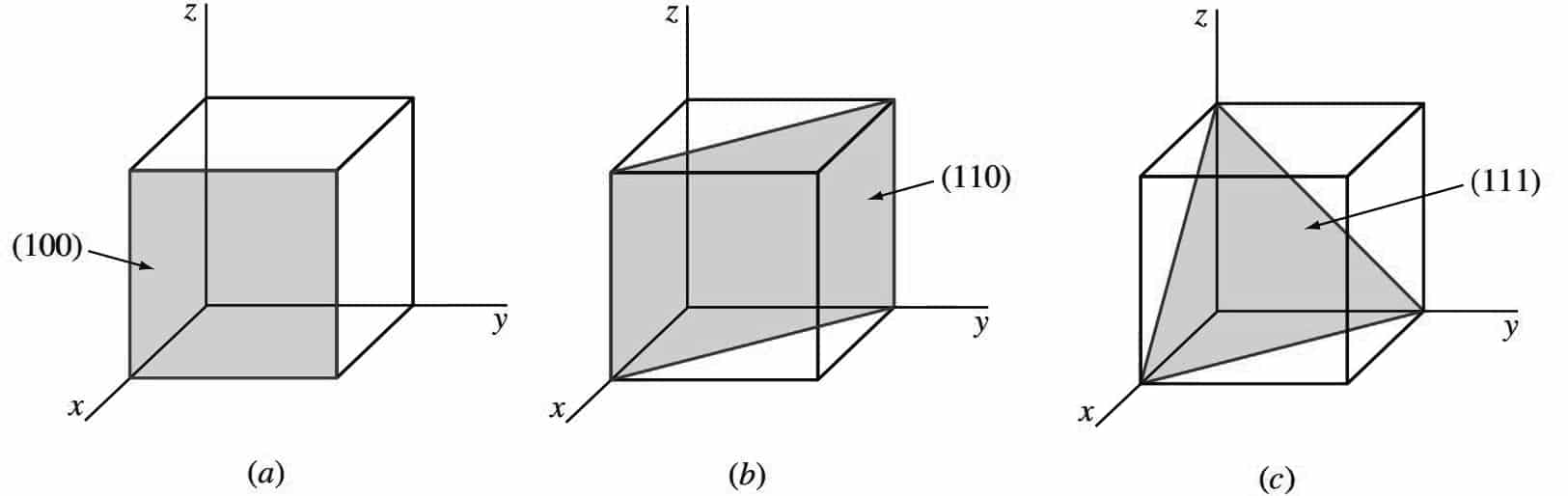
- Let us first consider the shaded crystal plane in Figure a, which has the intercepts 1, ∞, ∞ for the x, y, and z axes, respectively.
- We take the reciprocals of these intercepts to obtain the Miller indices, which are therefore 1, 0, 0.
- Since these numbers do not involve fractions, the Miller indices for this plane are (100), which is read as the one-zero-zero plane.
- Next, let us consider the second plane shown in Figure b. The intercepts of this plane are 1, 1, ∞.
- Since the reciprocals of these numbers are 1, 1, 0, which do not involve fractions, the Miller indices of this plane are (110).
- Finally, the third plane in the figure c has the intercepts 1, 1, 1, which give the Miller indices (111) for this plane
Let us Consider now the cubic crystal plane is shown in Figure below that has the intercepts 1/3, 2/3, 1.
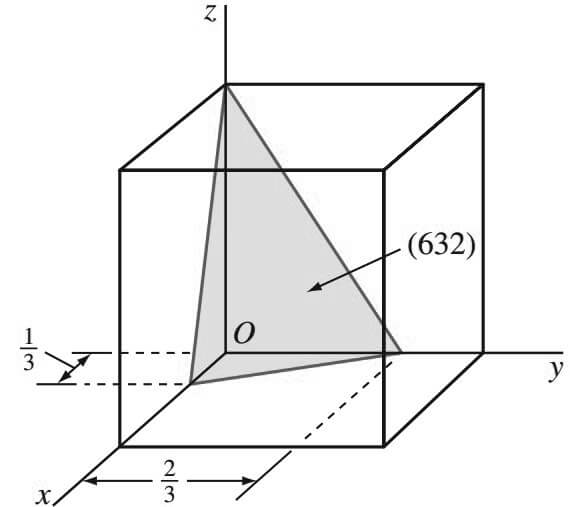
- The reciprocals of these intercepts are 3, 3/ 2 , 1.
- Since fractional intercepts are not allowed, these fractional intercepts must be multiplied by 2 to clear the 3/2 fractions.
- Thus, the reciprocal intercepts become 6, 3, 2, and the Miller indices are (6 3 2).
- Further examples of cubic crystal planes are discussed in the below Example Problem.
- If the crystal plane being considered passes through the origin so that one or more intercepts are zero, the plane must be moved to an equivalent position in the same unit cell, and the plane must remain parallel to the original plane.
- This is possible because all equispaced parallel planes are indicated by the same Miller indices.
- If sets of equivalent lattice planes are related by the symmetry of the crystal system, they are called planes of a family or form, and the indices of one plane of the family are enclosed in braces as {h k l} to represent the indices of a family of symmetrical planes.
For example, the Miller indices of the cubic surface planes (100), (010), and (001) are designated collectively as a family or form by the notation {100}.
Let us see an example problem to draw the crystallographic planes in cubic unit cells
Example problem on Crystallographic planes in Cubic unit cells
Draw the following crystallographic planes in cubic unit cells:
a. (1 0 1)
b. (1 1̄ 0)
c. (2 2 1)
d. Draw a (1 1 0) plane in a BCC atomic-site unit cell, and list the position coordinates of the atoms whose centers are intersected by this plane.
Answer:
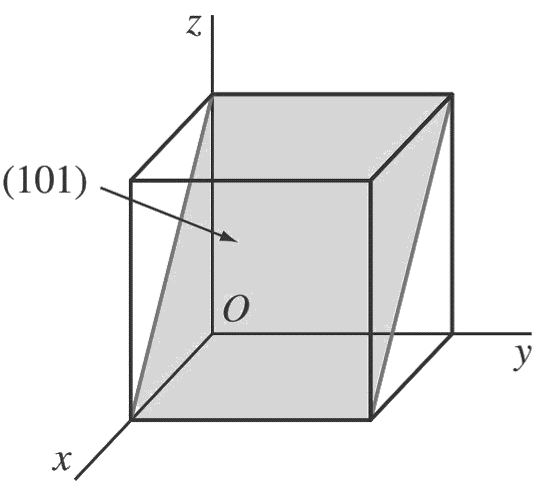
a. (1 0 1)
First, determine the reciprocals of the Miller indices of the (1 0 1) plane.
These are 1, ∞, 1. The (1 0 1) plane must pass through a unit cube at intercepts x = 1 and z = 1 and be parallel to the y axis.
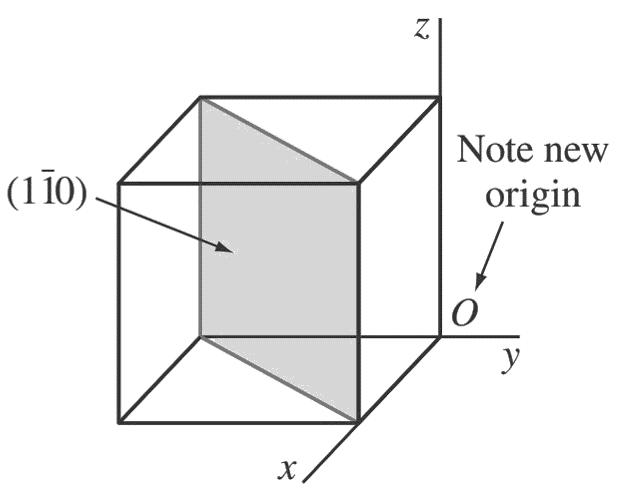
b. (1 1̄ 0)
First, determine the reciprocals of the Miller indices of the (1̄ 1 0) plane. These are 1, −1, ∞.
The (1̄ 1 0) plane must pass through a unit cube at intercepts x = 1 and y = −1 and be parallel to the z-axis.
Note that the origin of axes must be moved to the lower-right back side of the cube.
c. (2 2 1)
First, determine the reciprocals of the Miller indices of the (2 2 1) plane. These are 1/2, 1/2, 1.
The (2 2 1) plane must pass through a unit cube at intercepts x = 1/ 2 , y = 1/ 2 , and z = 1.
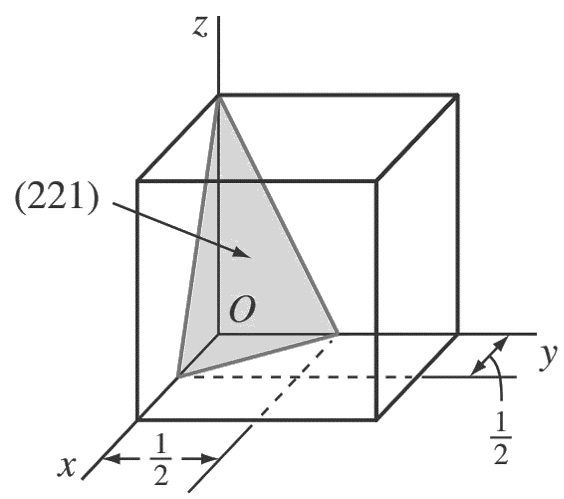
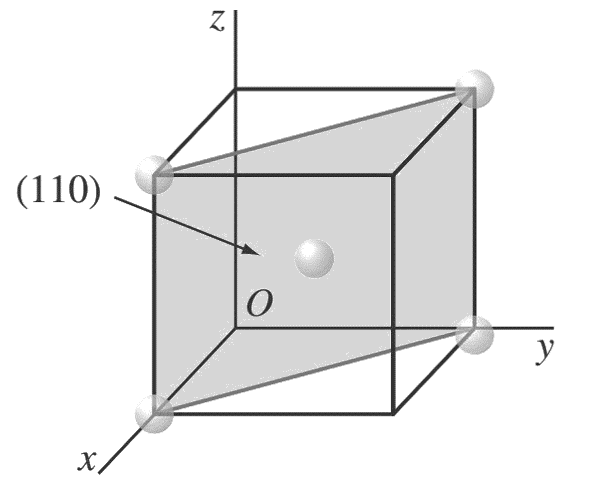
d.
Atom positions whose centers are intersected by the (1 1 0) plane are (1, 0, 0), (0, 1, 0), (1,0, 1), (0, 1, 1), and (1/2 ,1/2 ,1/2 ).
These positions are indicated by solid circles.
An important relationship for the cubic system, and only the cubic system, is that the direction indices of a direction perpendicular to a crystal plane are the same as the Miller indices of that plane.
For example, the [100] direction is perpendicular to the (100) crystal plane. In cubic crystal structures, the interplanar spacing between two closest parallel planes with the same Miller indices is designated dhkl, where h, k, and l are the Miller indices of the planes.
This spacing represents the distance from a selected origin containing one plane and another parallel plane with the same indices that are closest to it. For example, the distance between (110) planes 1 and 2, d110, in the below figure is AB
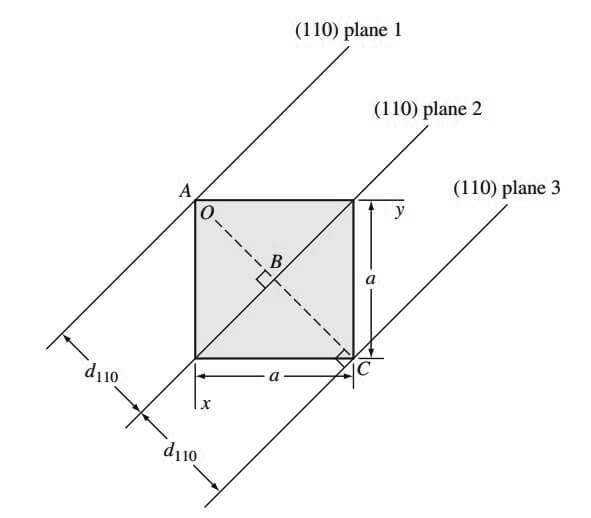
Also, the distance between (110) planes 2 and 3 is d110 and is length BC in the above figure.
From simple geometry, it can be shown that for cubic crystal structure
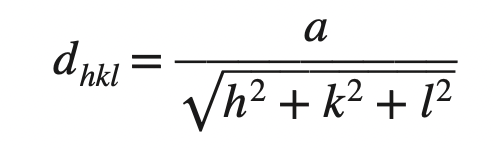
where
dhkl = interplanar spacing between parallel closest planes with Miller indices h, k, and l
a = lattice constant (edge of unit cube)
h, k, l = Miller indices of cubic planes being considered
Let us see an example problem to determine the Miller indices of the cubic crystallographic plane
Example problem on Miller indices of the cubic crystallographic plane
1. Determine the Miller indices of the cubic crystallographic plane shown in the below figure.
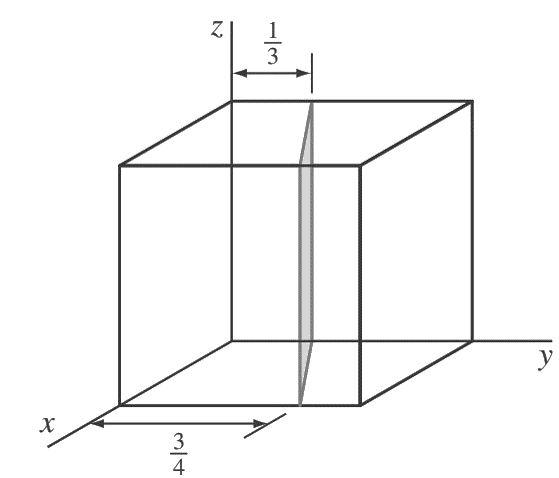

Answer:
First, transpose the plane parallel to the z-axis 1/4 unit to the right along the y axis as shown in the below figure.
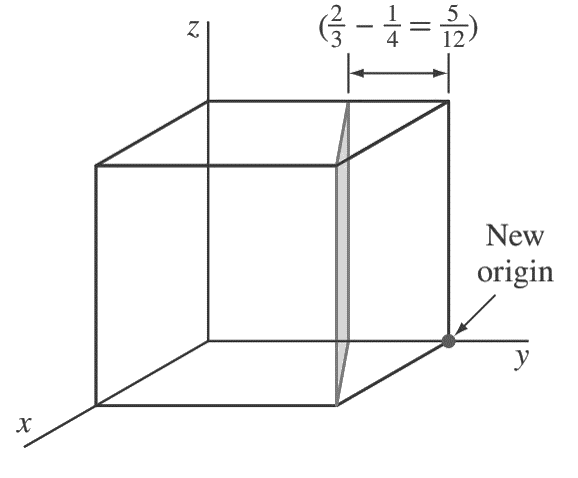
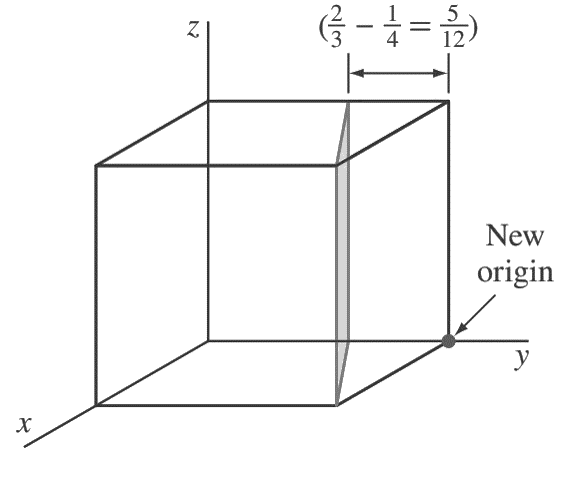
so that the plane intersects the x-axis at a unit distance from the new origin located at the lower-right back corner of the cube.
The new intercepts of the transposed plane with the coordinate axes are now (+1, −5/ 12, ∞).
Next, we take the reciprocals of these intercepts to give (1, −12/5, 0).
Finally, we clear the 12/5 fraction to obtain (5 12̄ 0) for the Miller indices of this plane.
2. Determine the Miller indices of the cubic crystal plane that intersects the position coordinates (1, 1/4, 0), (1, 1,/12 ), (3/4, 1,/1 4 ), and all coordinate axes.
Answer:
Solution
First, we locate the three position coordinates as indicated in the below figure at A, B, and C.
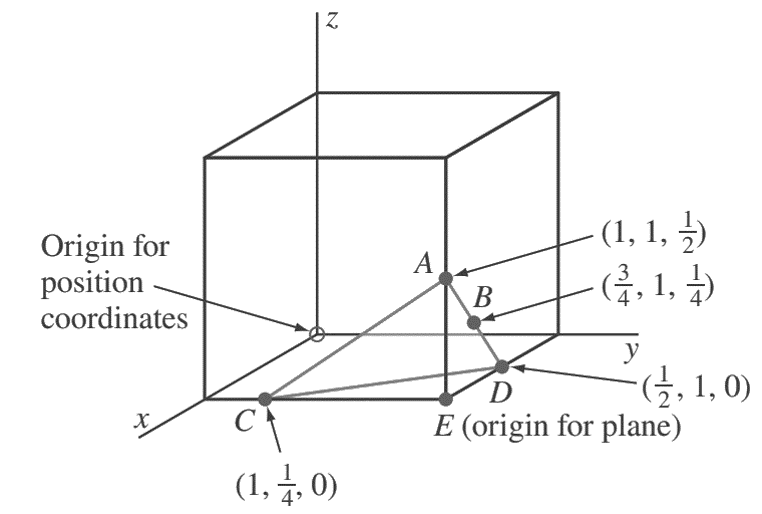
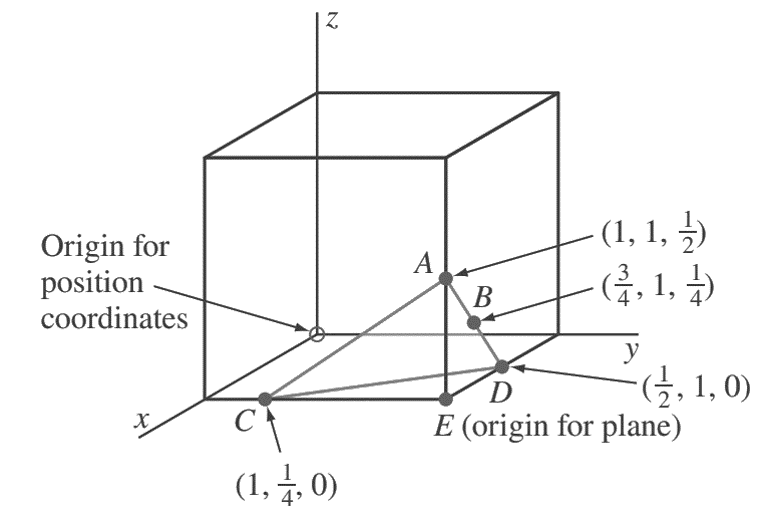
Next, we join A and B, extend AB to D, and then join A and C.
Finally, we join A to C to complete plane ACD.
The origin for this plane in the cube can be chosen at E, which gives axial intercepts for plane ACD at x = −1/2, y = −3/4, and z = 1/2.
The reciprocals of these axial intercepts are −2, −4/3, and 2.
Multiplying these intercepts by 3 clears the fraction, givingMiller indices for the plane of (6̄ 4̄ 6).
3. Copper has an FCC crystal structure and a unit cell with a lattice constant of 0.361 nm. What is its interplanar spacing d220?
Answer:
We know the interplanar spacing between parallel closest planes with Miller indices h, k, and l is given by
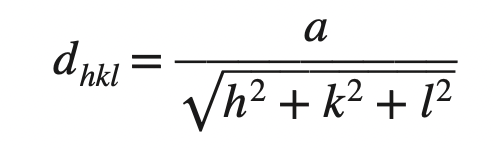
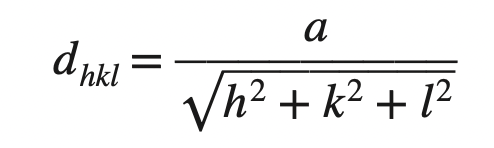
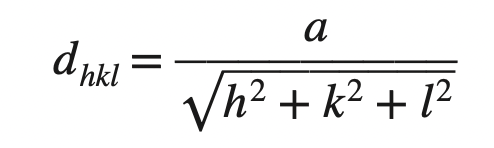
dhkl = 0.361 nm/ √((2)2 + (2)2 + (0)2)
dhkl = 0.128 nm
Indices for Crystal Planes in HCP Unit Cells
Crystal planes in HCP unit cells are commonly identified by using four indices instead of three. The HCP crystal plane indices, called Miller-Bravais indices, are denoted by the letters h, k, i, and l and are enclosed in parentheses as (h k i l).
This four-digit hexagonal index is based on a coordinate system with four axes, as shown in the below Figure in an HCP unit cell.
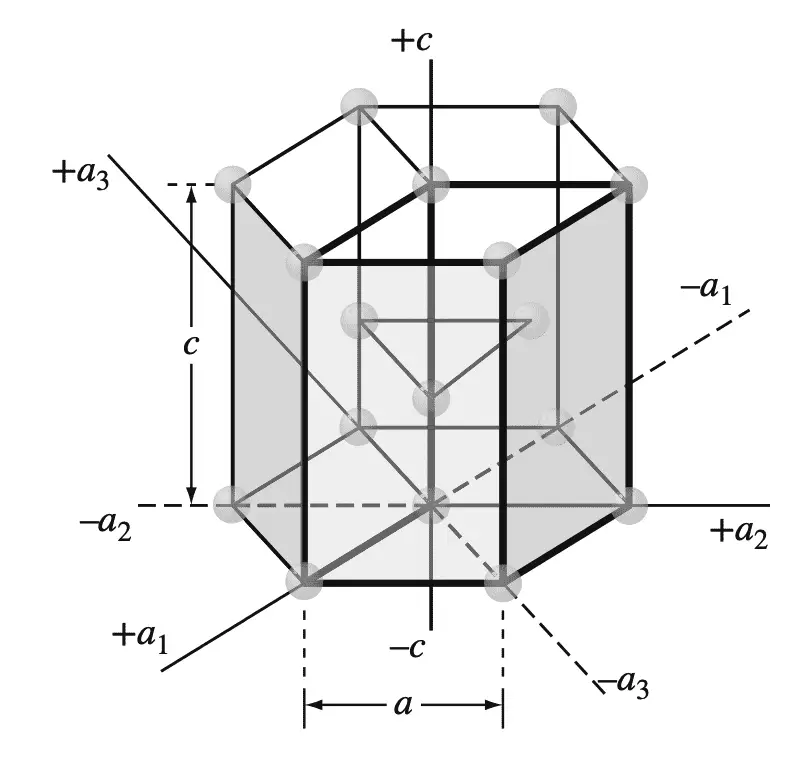
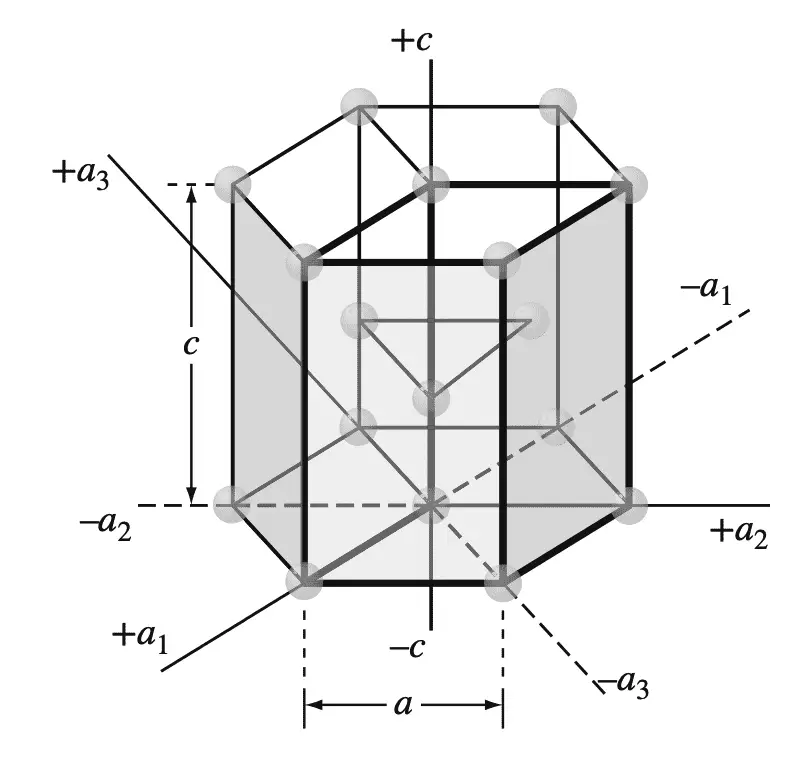
The four coordinate axes (a1, a2, a3, and c) of the HCP crystal structure.
There are three basal axes, a1, a2, and a3, which make 120° with each other. The fourth axis or c axis is the vertical axis located at the center of the unit cell.
The unit of measurement along the a1, a2, and a3 axes is the distance between the atoms along these axes and is indicated in the above Figure.
In the discussion of HCP planes and directions, we will use both the “unit cell” and the “larger cell” for the presentation of concepts. The unit of measurement along the c axis is the height of the unit cell. The reciprocals of the intercepts that a crystal plane makes with the a1, a2, and a3 axes give the h, k, and i indices, while the reciprocal of the intercept with the c axis gives the l index.
Basal Planes
The basal planes of the HCP unit cell are very important planes for this unit cell and are indicated in the below figure.
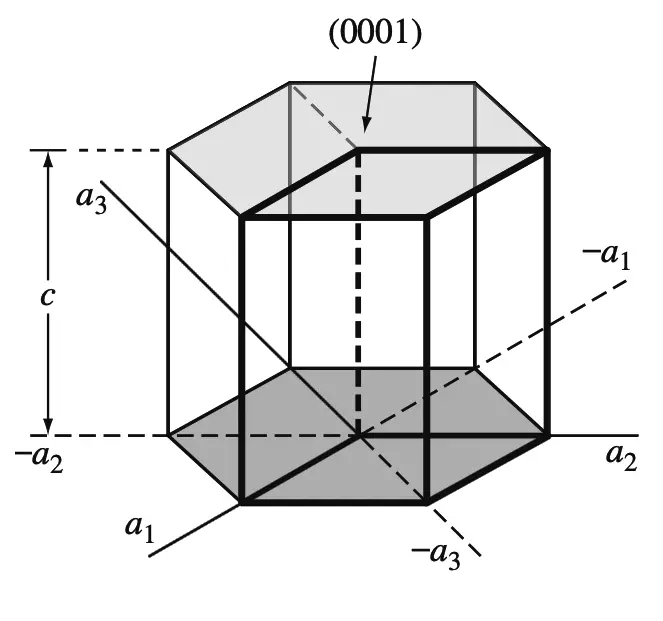

Since the basal plane on the top of the HCP unit cell in the above figure is parallel to the a1, a2, and a3 axes, the intercepts of this plane with these axes will be at infinity.
Thus,
a1intercept = ∞,
a2intercept = ∞,
a3intercept = ∞.
The c axis, however, is unity since the top basal plane intersects the c axis at a unit distance,
Cintercept = 1
Taking the reciprocals of these intercepts gives the Miller-Bravais indices for the HCP basal plane.
Thus h = 0, k = 0, i = 0, and l = 1.
The HCP basal plane is, therefore, a zero-zero-zero-one or (0001) plane.
Prism Planes
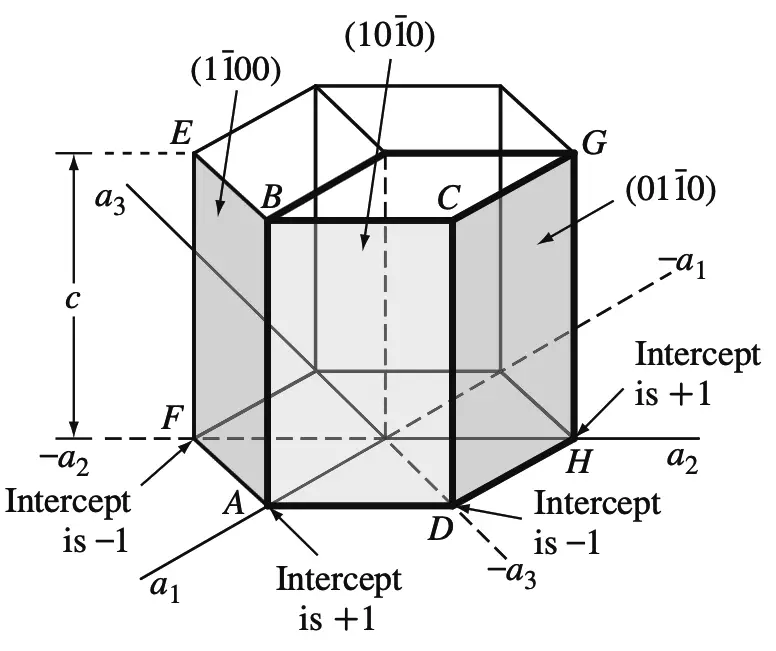
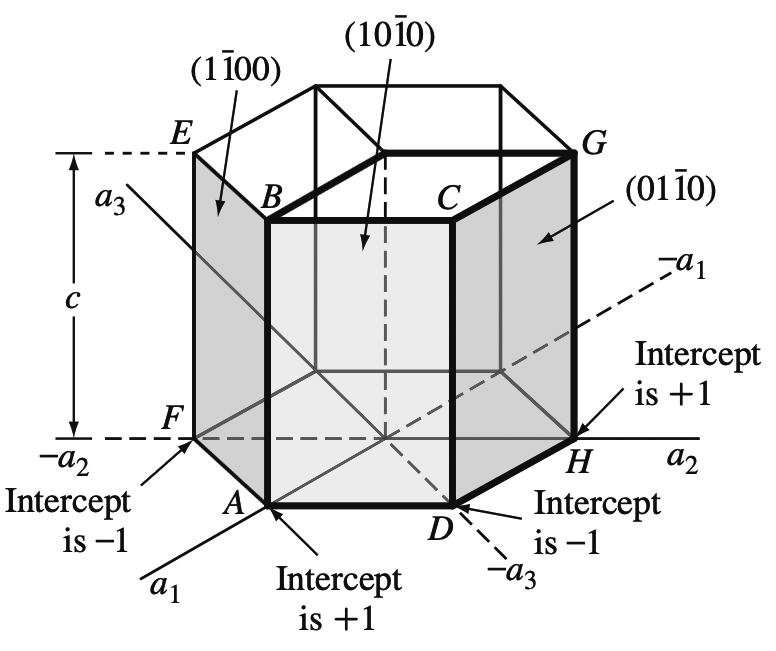
Miller-Bravais indices of hexagonal crystal planes: (a) basal planes and (b) prism planes
Using the same method, the intercepts of the front prism plane (ABCD) as shown in the above figure are a1intercept = +1
a2intercept = ∞
a3intercept = −1
cintercept = ∞
Taking the reciprocals of these intercepts gives h = 1, k = 0, i = −1, and l = 0, or the (1 0 1̄ 0) plane.
Similarly, the ABEF prism plane in the above figure has the indices (1 1̄ 0 0) and the DCGH plane the indices (0 1 1̄ 0).
All HCP prism planes can be identified collectively as the {1 0 1̄ 0} family of planes.
Sometimes HCP planes are identified only by three indices (h k l) since h + k = −i.
However, the (h k i l) indices are used more commonly because they reveal the hexagonal symmetry of the HCP unit cell.
Direction Indices in HCP Unit Cells
Directions in HCP unit cells are also usually indicated by four indices u, v, t, and w enclosed by square brackets as [u v t w].
The u, v, and t indices are lattice vectors in the a1, a2, and a3 directions, respectively, and the w index is a lattice vector in the c direction.
To maintain uniformity for both HCP indices for planes and directions, it has been agreed that u + v = −t for directions.
Let us now determine the Miller-Bravais hexagonal indices for the directions a1, a2, and a3, which are the positive basal axes of the hexagonal unit cell.
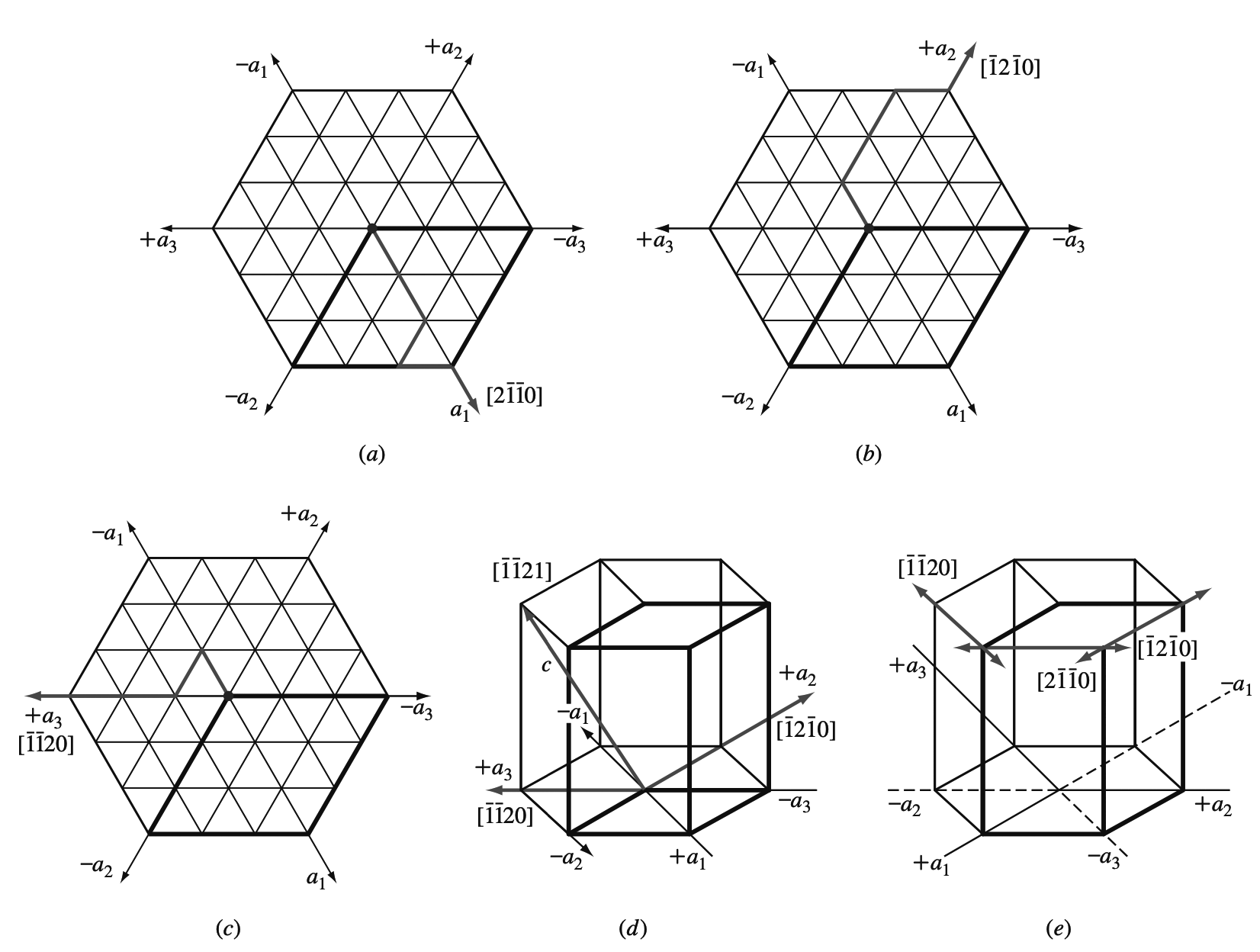
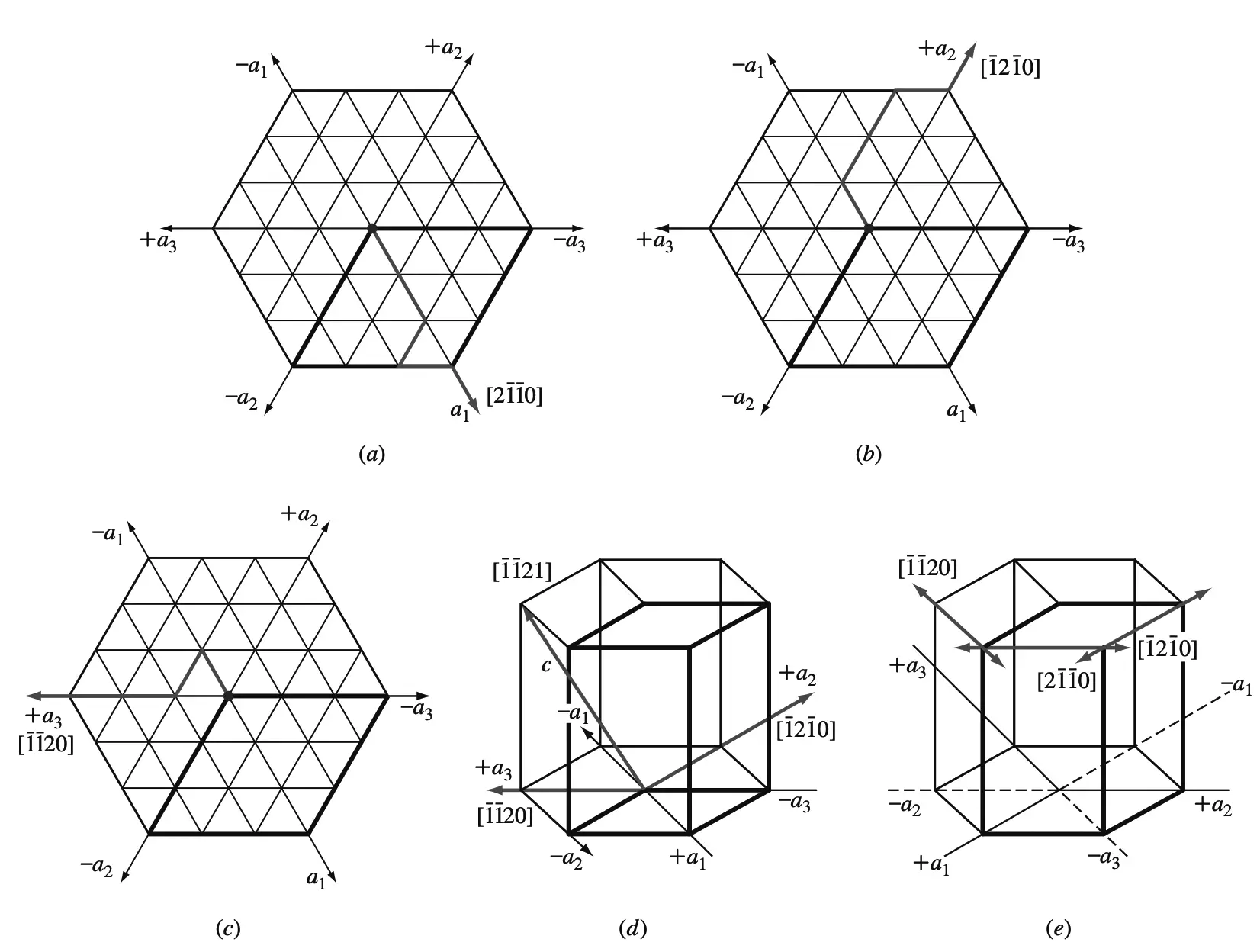
(a) +a1 axis direction on the basal plane,
(b) +a2 axis direction on the basal plane,
(c) +a3 direction axis on the basal plane,
(d) +a3 direction axis incorporating c axis.
(e) Positive and negative Miller-Bravais directions are indicated in simple hexagonal crystal structure on the upper basal plane.
The a1 direction indices are given in Figure a, the a2 direction indices in Figure b, and the a3 direction indices in Figure c.
If we need to indicate a c direction also for the a3 direction, this is shown in Figure d.
Figure e summarizes the positive and negative directions on the upper basal plane of the simple hexagonal crystal structure.

The concept is well elaborated, and helpful to my learning.
EXAMPLES SHOULD BE ADDED
Sure we will add it and let you know. Thanks for the feedback.