In Fluid Dynamics, A jet is a liquid stream projected into a surrounding medium or an object from the nozzle. Jet propulsion means the propulsion or movement of the bodies such as ships, aircraft, and rockets with the help of a jet. The reaction of the jet coming out from the orifice provided in the bodies is used to move the bodies. Let us Understand the Jet propulsion Principle and determine the essential parameters of Jet Propulsion of Ships such as the propelling force of the ships, and the efficiency of Jet propulsion.

Jet Propulsion
As we mentioned above Jet propulsion means the propulsion or movement of the bodies such as ships, aircraft, and rockets with the help of a jet. The reaction of the jet coming out from the orifice provided in the bodies is used to move the bodies.
A jet of fluid coming out from an orifice or nozzle, when strikes a plate, exerts a force on the plate. The magnitude of the force exerted on the plate can be determined depending on whether the plate is flat, inclined, curved, stationary or moving. This force exerted by the jet on the plate is called as “action of the jet’.
But according to Newton’s third law of motion, every action is accompanied by an equal and opposite reaction. Hence the jet while coming out of the orifice or nozzle exerts a force on the orifice or nozzle in the opposite direction in which the jet is coming out. The magnitude of the force exerted is equal to the ‘action of the jet’. This force which is acting on the orifice or nozzle in the opposite direction is called the ‘reaction of the jet’.
If the body in which the orifice or nozzle is fitted, is free to move, the body will start moving in the direction opposite to the jet. The following cases are important where this principle is used :
- Jet propulsion of a tank to which the orifice is fitted
- Jet propulsion of ships
Let us discuss these two cases in a detailed manner.
1. Jet Propulsion of a Tank with an Orifice
Consider a large tank fitted with an orifice in one of its sides as shown in the following figure.
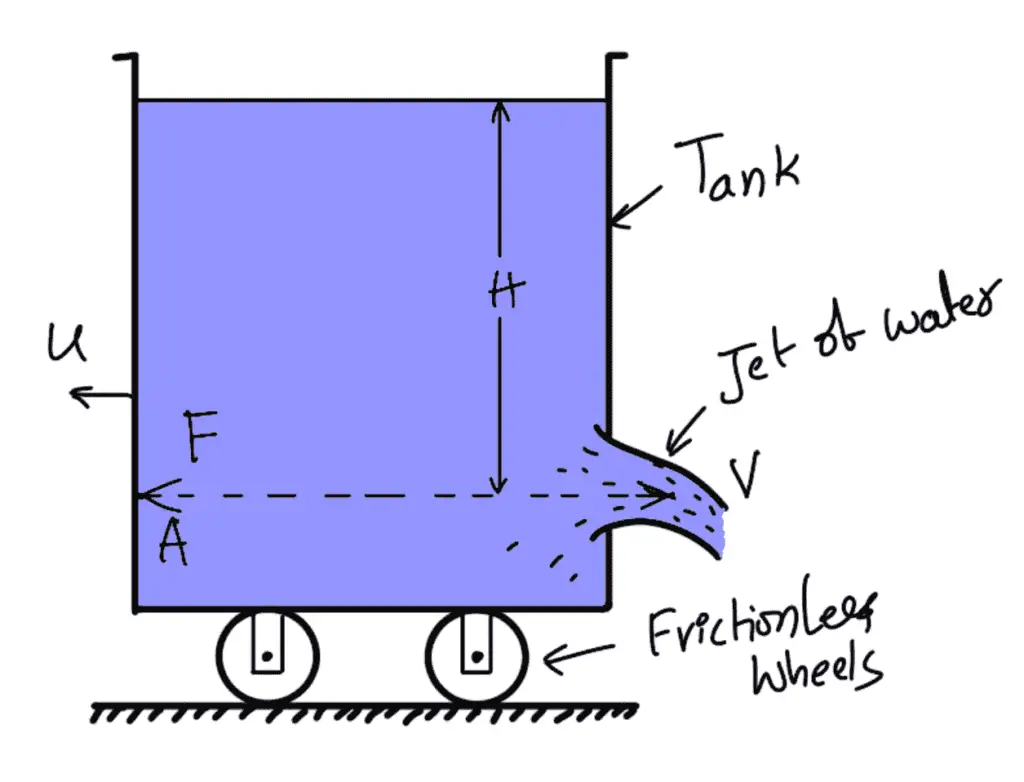
Let
H= Constant head of water in the tank from the centre of the orifice,
a = Area of the orifice,
V = Velocity of the jet of water,
Cv = Co-efficient of the velocity of the orifice.
Then
V = Cv √(2gH)
And the mass of water coming out from the orifice per second = ρ × Volume per second
mwater = ρ × (Area × Velocity)
mwater = ρ × a × V
Force acting on the water is equal to the rate of change of momentum.
F = Mass per second x [Change of velocity]
F = Mass per second x [Final velocity – Initial velocity]
Please note that Here the change of velocity is to be taken as final minus initial as we are finding force on water and not force exerted by water. The initial velocity of water in the tank is zero and the final velocity of water when it comes out in the form of the jet is equal to V.
F = ρaV [V-0]
F = ρaV2
Thus, F is the force exerted on the jet of water. This jet of water will exert a force on the tank which is equal to F but opposite in direction as shown in the above figure.
The force will be acting at A, the point on the tank in the horizontal line of the centre of the orifice. If the tank is free to move or the tank is fitted with a frictionless wheel, it will start moving with some velocity say, “u’ in the direction opposite to the direction of the jet. When the tank starts moving, the velocity of the jet with which it comes out of the orifice will not be equal to V but it will be equal to the relative velocity of the jet with respect to the tank.
Hence if
V = Absolute velocity of the jet
u = Velocity of tank
Vr = Velocity of jet with respect to tank
Then
Vr = Vectorial difference of absolute velocity (V) and velocity of the tank (u)
Vr = V – (- u) (as u is in opposite direction to V hence the velocity of the tank is taken as – u)
Vr = V + u
Hence when the tank is moving, the velocity with which the jet comes out from the orifice is (V + u).
Mass of water coming out from the orifice per sec = ρ × a × Velocity with which water comes out
mwater = ρ × a × Vr
mwater = ρa(V+ u)
Force exerted on the tank is given as
Fx = Mass of water coming out from orifice per second × [Change of velocity]
Fx = ρa(V + u) × [(V + u) – u]
Fx = ρa [V+ u] × [V]
Fx = ρa [V+ u] V
Thus, the force given by equation (17.30) is used for propelling the tank.
Work done on the moving tank by jet per second = Fx × u
W = pa(V + u) × V × u
Efficiency of Jet Propulsion
The efficiency of propulsion is given as,
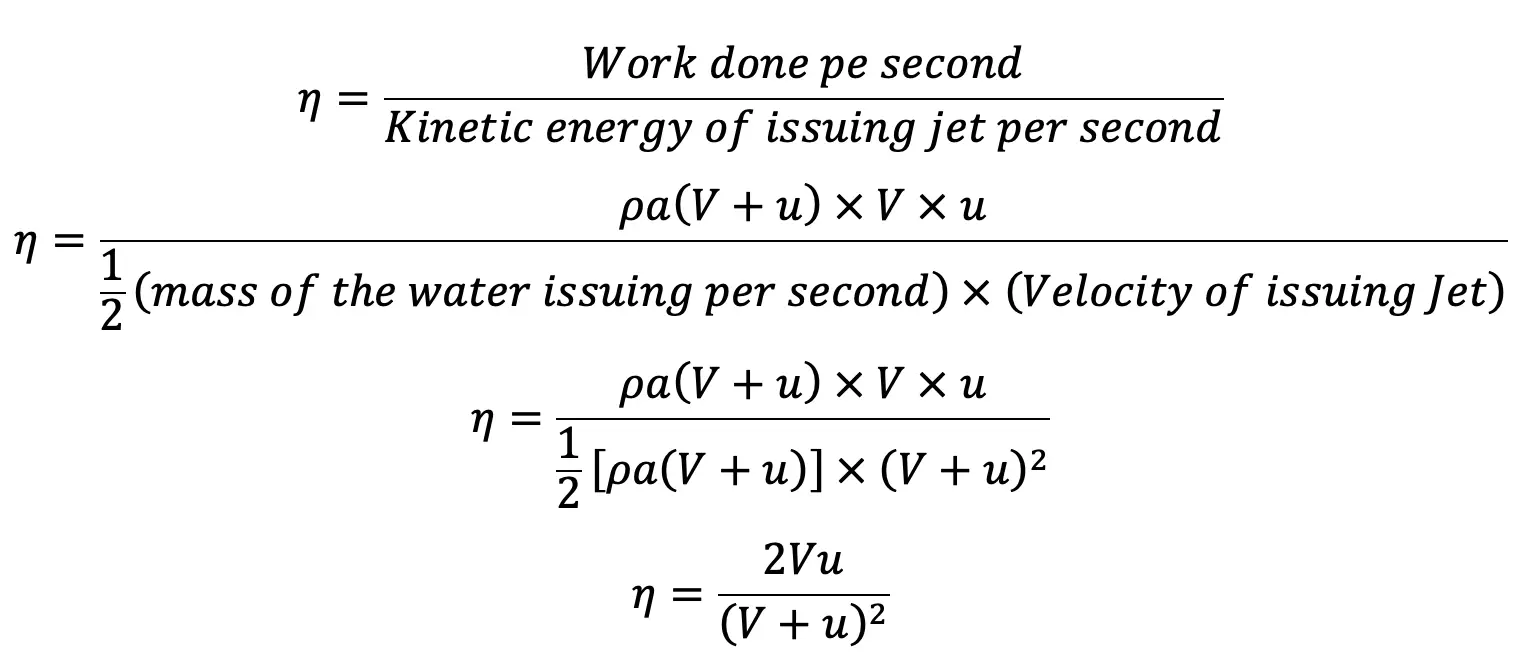
Condition for Maximum Efficiency and Expression for Maximum η
For a given value of V, the efficiency will be maximum when dη/du = 0
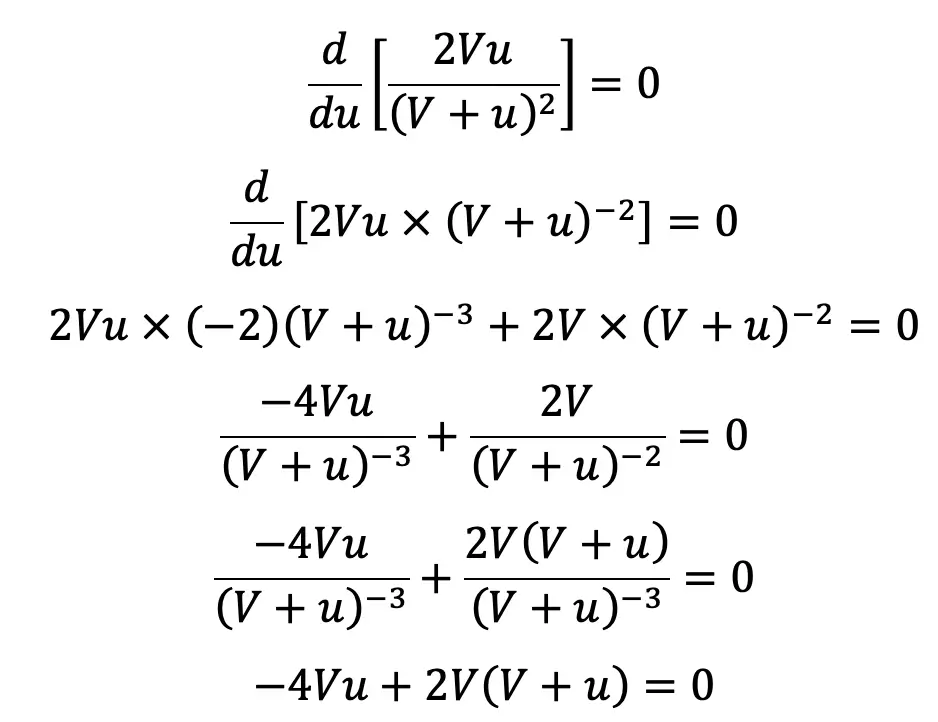
Dividing by 2V, we get
-2u + (V + u) = 0
-u + V= 0
u = V
….. Equation (b)
This Equation u = V is the condition for maximum efficiency. Substituting this equation in equation (a), the value of maximum efficiency is obtained as
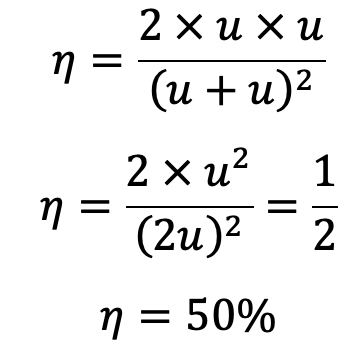
2. Jet Propulsion of Ships
By the application of the jet propulsion principle, a ship is driven through water. A jet of water which is discharged at the back (also called stern) of the ship, exerts a propulsive force on the ship. The ship carries centrifugal pumps which draw water from the surrounding sea. This water is discharged through the orifice provided at the back of the ship in the form of a jet. The reaction of the jet coming out at the back of the ship propels the ship in the opposite direction of the jet. The water from the surrounding sea by the centrifugal pump is taken by the following two ways :
- Through inlet orifices which are at right angles to the direction of the motion of the ship
- Through the inlet orifices, which are facing the direction of motion of the ship
1st Case: Jet propulsion of the ship when the inlet orifices are at right angles to the direction of the motion of the ship
The following figure shows a ship which is having inlet orifices at right angles to its direction.
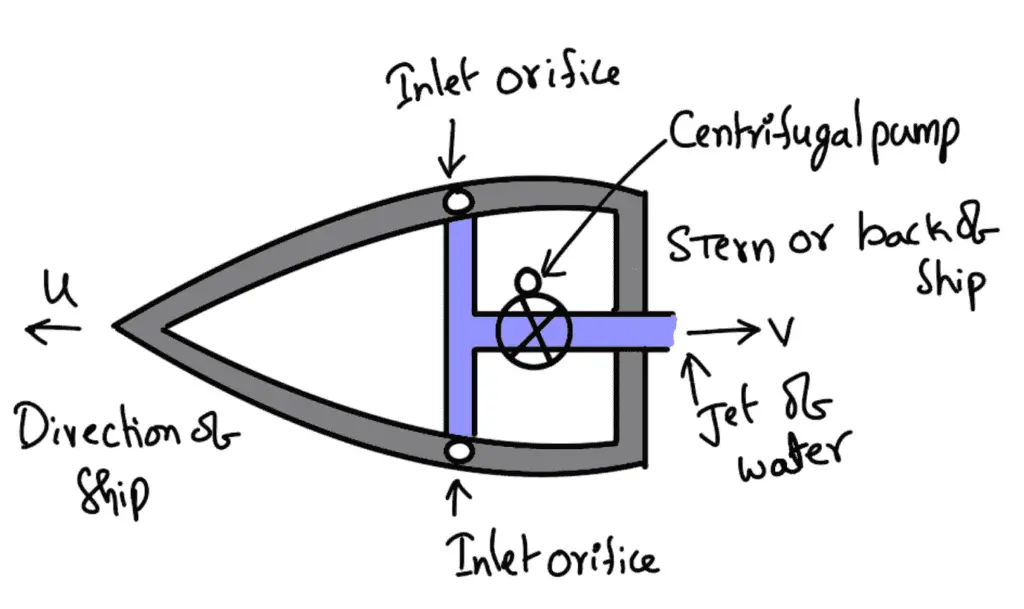
Let
V = Absolute velocity of jet of water coming at the back of the ship
u = Velocity of the ship
Vr = Relative velocity of jet with respect to ship = (V + u)
As the velocity, V and u are in opposite directions and hence relative velocity will be equal to the sum of these two velocities.
Mass of water issuing from the orifice at the back of the ship = ρaVr = ρa(V + u)
where a = Area of the jet of water Propulsive force exerted on the ship
The Propelling force F will be
F = Mass of water issuing per sec × Change of velocity
F = ρa(V + u) [Vr – u]
F = ρa(V + u) [(V + u) – u]
F = ρa(V + u) × V
….. Equation (d)
Work done per second
W = F × u
W = ρa(V + u) × V × u
The efficiency of propulsion, the condition of maximum efficiency and the expression for maximum
efficiency is given by equations (a), (b) and (c) respectively.
- When the inlet orifices are at right angles to the direction of motion of the ship, then this case is also known as water is drawn AMID SHIP which means the water is drawn at the middle of the ship.
- The centrifugal pump draws the water from the surrounding sea and discharges it through the orifice. The kinetic energy of the issuing jet is ½ × mass × velocity2
K.E = ½ [ρa(V + u)] × [V + u]2
K.E = ½ ρa(V + u)3
This energy is provided by a centrifugal pump i.e., work is done by a pump to provide this energy.
Example Problem on Jet Propulsion
Let us solve an Example to Calculate the propelling force of the ships, Power required to drive the pump and the efficiency of Jet propulsion when the inlet orifices are at right angles to the direction of the motion of the ship
Problem Statement: The water in a jet-propelled ship is drawn amid ship and discharged at the back with an absolute velocity of 20 m/s. The cross-sectional area of the jet at the back is 0.02 m2 and the ship is moving in seawater at a speed of 30 km/hour. Determine :
(i) Propelling force on the Ship
(ii) Power required to drive the pump
(iii) Efficiency of the jet propulsion
Answer:
Given data
Water is drawn amidships means water is drawn at the middle of the ship and inlet orifices are at right angles to the motion of the ship.
Absolute velocity of jet, V = 20 m/s
Area of the jet, a = 0.02 m2
Speed of ship, u = 30 km/hr = (30 × 1000) ÷ (60 × 60) = 8.33 m/s
(i) Propelling force on the Ship
Propelling force is given by equation (d) as
F = ρa(V + u) × V
F = 1000 × 0.02(20 + 8.33) × 20
F = 11332 N
(ii) Power required to drive the pump
The Power required to drive the pump in kW = Work done per sec ÷ 1000
P = (F × u) ÷ 1000
P = 11332 × 8.333 ÷ 1000
P = 94.4 kW
(iii)Efficiency of the jet propulsion
The Efficiency of the jet propulsion is given by equation (a) as
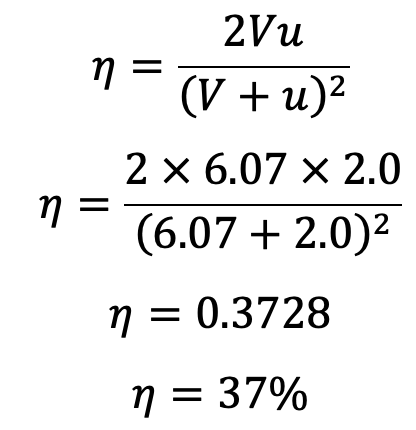
The Efficiency of jet propulsion is 37%.
2nd Case: Jet propulsion of ship when the inlet orifices face the direction of motion of the ship
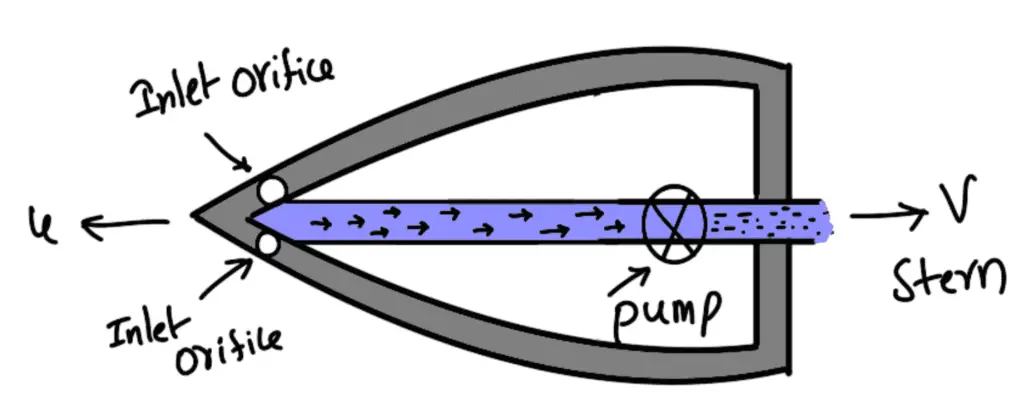
The above Figure shows a ship which is having inlet orifices facing the direction of the motion of the ship. In this case, the expression for propelling force and work done per second will be the same as in the 1st case in which inlet orifices are at right angles to the ship. But the energy supplied by the jet will be different, as in this case, the water enters with a velocity equal to the velocity of the ship, i.e., with a velocity u.
Hence the expression for the energy supplied by the jet.
Input Energy = ½ (Mass of water supplied per sec) × [Vr2 – u2]
Input Energy = ½ (ρ × a × Vr) × [Vr2 – u2]
Where Vr = (V + u)
The kinetic energy supplied by the jet we can write
K.E = ½ (ρ × a × Vr) × [Vr2 – u2]
K.E = ½ (ρ × a × (V + u)) × [(V + u)2 – u2]
K.E = ½ ρa × (V + u)× [(V + u)2 – u2]
….. Equation (e)
The efficiency of propulsion is
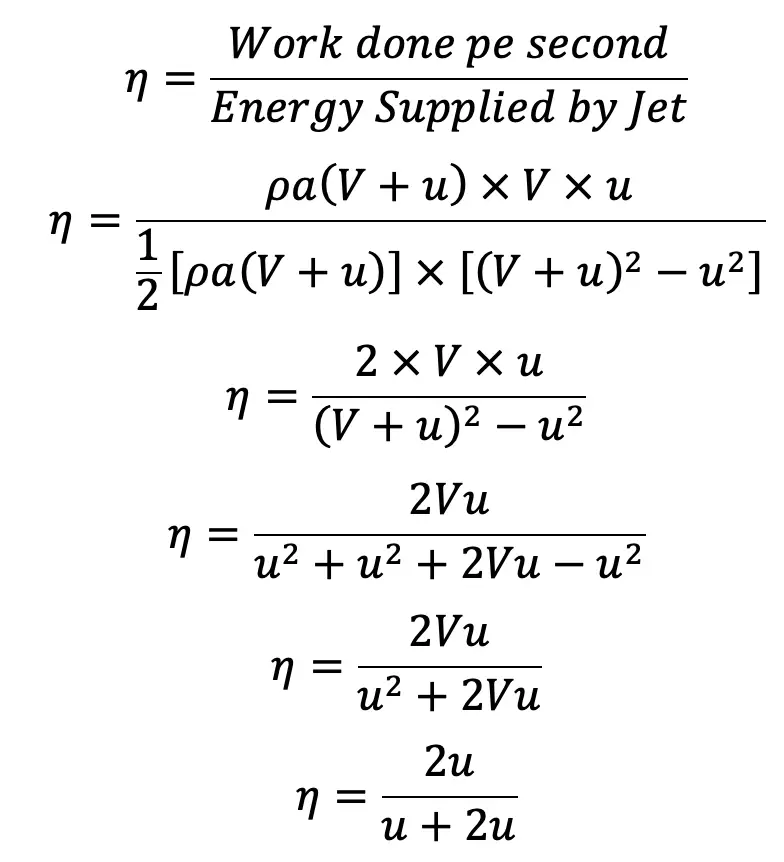
Example Problem on Jet Propulsion
Let us solve an Example to Calculate the propelling force of the ships, the Power required to drive the pump and the efficiency of Jet propulsion when the inlet orifices face the direction of motion of the ship.
Problem Statement: The water in a jet-propelled ship is drawn through inlet openings facing the direction of motion of the ship. The boat is moving in seawater at a speed of 30 km/hour. The absolute velocity of the jet of the water discharged at the back is 20 m/s and the area of the jet of water is 0.03 m2. Please find the propelling force and the efficiency of the Propulsion.
Answer:
Speed of ship, u = 30 km/hr = (30 × 1000) ÷ (60 × 60) = 8.33 m/s
Absolute velocity of jet, V = 20 m/s
Area of the jet, a = 0.03 m2
(i) Propelling force on the Ship
Propelling force is given by equation (d) as
F = ρa(V + u) × V
F = 1000 × 0.03(20 + 8.33) × 20
F = 16997.98 N
(ii)Efficiency of the jet propulsion
The Efficiency of the jet propulsion is given by equation (a) as
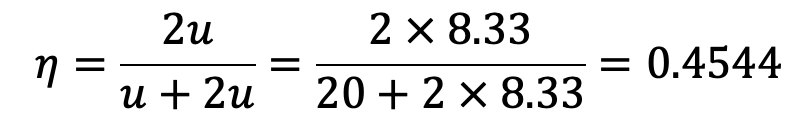
The Efficiency of jet propulsion is 45%.
This is all about the Jet Propulsion of a Ship or boat. Let us know what you think about this article in the comment section below.

Leave a Reply