The study of the corrosion of metals has been centered on equilibrium conditions and the tendency of metals to corrode, which has been related to the standard electrode potentials of metals. However, corroding systems are not at equilibrium, and thus thermodynamic potentials do not tell us about the rates of corrosion reactions. The kinetics of corroding systems are very complex and are not completely understood. Let us examine some of the basic aspects of corrosion kinetics and see how we can calculate the Corrosion Rate.

Uniform Corrosion Rate
The amount of metal uniformly corroded from an anode or electroplated on a cathode in an aqueous solution in a time period can be determined by using Faraday’s equation of general chemistry.
Do you know?
Michael Faraday (1791–1867) is an English scientist who made basic experiments in electricity and magnetism. He made experiments to show how ions of a compound migrated under the influence of an applied electric current to electrodes of opposite polarity.
Faraday’s Equation States that
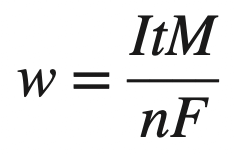
where
w = weight of the metal in grams (g), corroded or electroplated in an aqueous solution in time t in seconds (s)
I = current flow in Amps (A)
M = atomic mass of the metal, g/mol
n = number of electrons/atom produced or consumed in the process
F = Faraday”s constant = 96, 500 C/mol or 96,500 A · s/mol
Sometimes the uniform aqueous corrosion of metal is expressed in terms of current density I, which is often expressed in amperes per square centimeter.
Replacing I with it converts the above equation as follows
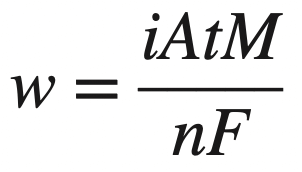
where
i = current density, A/cm2
A = area, (cm2 if the centimeter is used for length)
M = atomic mass of the metal, g/mol
n = number of electrons/atom produced or consumed in the process
F = Faraday”s constant = 96, 500 C/mol or 96,500 A · s/mol
Let us solve an example problem to calculate the Corrosion rate using the above equation.
Example Problem to Calculate Corrosion Rate
1. A copper electroplating process uses 15 A of current by chemically dissolving (corroding) a copper anode and electroplating a copper cathode. If it is assumed that there are no side reactions, how long will it take to corrode 8.50 g of copper from the anode?
Answer:
The time to corrode the copper from the anode can be determined from the above fraraday’s equation as follows
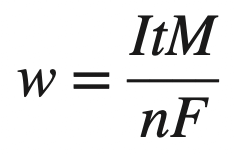
Let us write it in terms of t
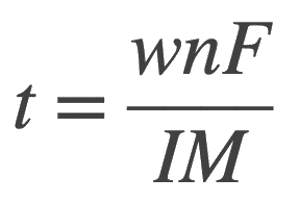
In this case from the given problem we have
w = 8.5 g
n = 2 for Cu → Cu2+ + 2e−
F = 96,500 A⋅s/mol
M = 63.5 g/mol for Cu
I = 15 A
t = ? (in seconds)
Let us substitute these values in the above relation, we get
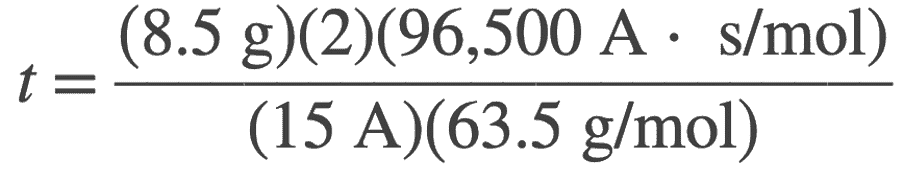
t = 1722 s
t = 28.7 minutes
2. A mild steel cylindrical tank 1 m high and 50 cm in diameter contains aerated water to the
60 cm level and shows a loss in weight due to corrosion of 304 g after six weeks.
(a) Calculate the corrosion current
(b) Calculate the current density involved in the corrosion of the tank.
Assume uniform corrosion on the tank’s inner surface and that the steel corrodes in the same
manner as pure iron.
Answer: a
We will use the following equation re-written from the above faraday’s equation to solve for the corrosion current:
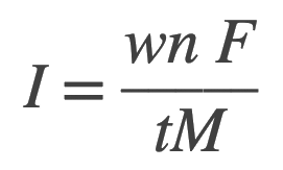
from the given data, we have
w = 304 g
n = 2 for Fe → Fe2+ + 2 e−
F = 96,500 A⋅s/mol
M = 55.85 g/mol for Fe
t = 6 weeks = 6×7×24×60 = 3.63×106s
I = ? A
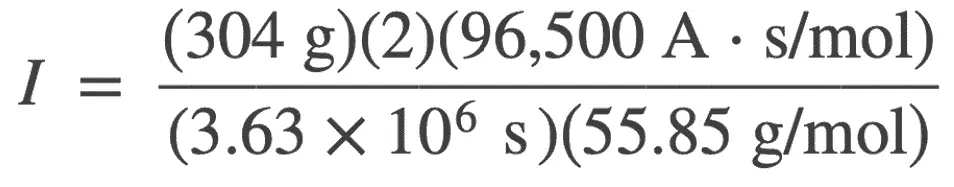
I = 0.289A
Answer: b
The current density is
Area of corroding surface of tank = area of sides + area of the bottom
Area of corroding surface of tank = πDh + πr2
Area of corroding surface of tank = π(50 cm)(60 cm) + π(25 cm)2
Area of corroding surface of tank = 9420 cm2 + 1962 cm2 = 11,380 cm2
Let us substitute in the above relation I
i =0.289 A /11,380 cm2 = 2.53 × 10−5A/cm2
The current density is 2.53 × 10−5A/cm2.
In experimental corrosion work, the uniform corrosion of a metal surface exposed to a corrosive environment is measured in a variety of ways.
One common method is to measure the weight loss of a sample exposed to a particular environment and then after a period of time express the corrosion rate as a weight loss per unit area of exposed surface per unit time. For example, uniform surface corrosion is often expressed as milligram weight loss per square decimeter per day (mdd).
3. The wall of a steel tank containing aerated water is corroding at a rate of 54.7 mdd. How long will it take for the wall thickness to decrease by 0.50 mm?
Answer:
The corrosion rate is 54.7 mdd, or 54.7 mg of metal is corroded on each square decimeter of surface per day.
Corrosion rate in g/(cm2⋅day) = (54.7 × 10−3 g) / (100 cm2 ⋅ day) = 54.7 × 10−4 g/(cm2⋅day)
The density of Fe = 7.87 g/cm3.
Dividing the corrosion rate in g/(cm2·day) by the density gives the depth of corrosion per day.
The depth of corrosion per day = (54.7 × 10−4 g/(cm2⋅day)) / 7.87 g/cm3
The depth of corrosion per day = 0.695 × 10−4 cm/day
The number of days required for a decrease in 0.50 mm can be obtained by a ratio as
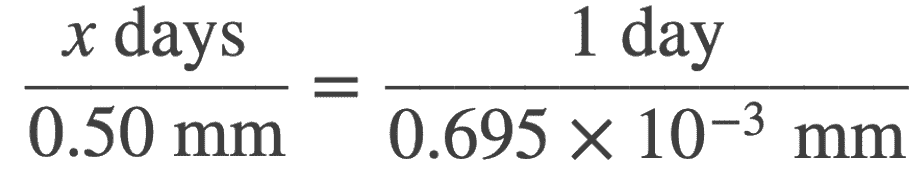
x = 719days
Another commonly used method is to express corrosion rate in terms of loss in depth of material per unit time. Examples of corrosion rates in this system are millimeters per year (mm/yr) and mils (1 mil = 0.001 in) per year (mils/yr). For uniform electrochemical corrosion in aqueous environments, the corrosion rate may be expressed as a current density.
Let us solve an example on this method to calculate the Corrosion Rate
4. A sample of zinc corrodes uniformly with a current density of 4.27 × 10−7 A/cm2 in an aqueous solution. What is the corrosion rate of the zinc in milligrams per decimeter per day? The reaction for the oxidation of zinc is Zn → Zn2+ + 2e−.
Answer:
To make the conversion from current density to mdd, we will use Faraday’s equation to calculate the milligrams of zinc corroding on an area of 1 dm2/day (mdd).
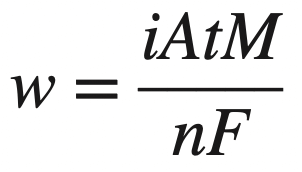
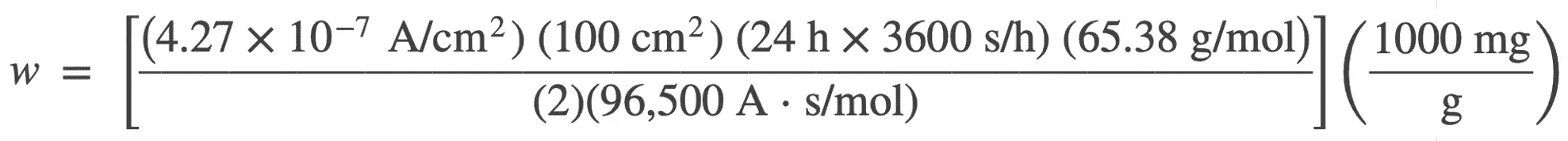
w = 1.25 mg of zinc which corrodes on an area of 1 dm2 in 1 day
or the corrosion rate is 1.25 mdd
Conclusion
We have discussed how to calculate the Corrosion rate using Faraday’s equation, also solve 4 example problems on calculating Corrosion Rate. Let us know what do you think about this article in the comment section below.

Leave a Reply