Do you know the difference between the Centroid and Centre Of Gravity?
In simple words, the Centroid is the geometrical centre of the body, whereas the centre of gravity is the point where the total weight of the body focuses upon. Let us see How we can Calculate the Centroid and Centre Of Gravity for any object.

Center of Gravity
The Center of gravity of a material body is a point that may be used for a summary description of gravitational interactions. The centre of gravity of anybody can also be determined by a simple physical procedure.
Centroid
Whereas the centroid of a plane figure is the arithmetic mean position of all the points in the figure. Informally, Centroid is the point at which a cutout of the shape could be perfectly balanced on the tip of a pin.
Finding Centroid and Centre Of Gravity of an Object
Consider the suspended body shown in the below figure.
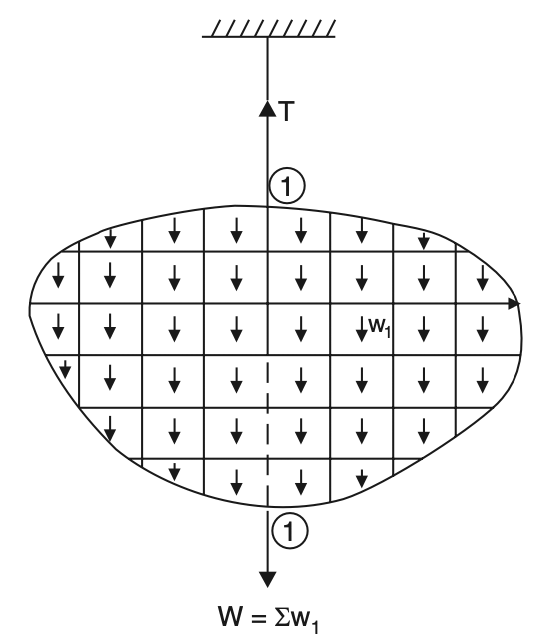
The self-weight of various parts of this body is acting vertically downward. The only upward force is the force T in the string.
To satisfy the equilibrium condition the resultant weight of the body W must act along the line of string 1–1.
Now, if the position is changed and the body is suspended again as shown in the below figure, it will reach an equilibrium condition in a particular position.
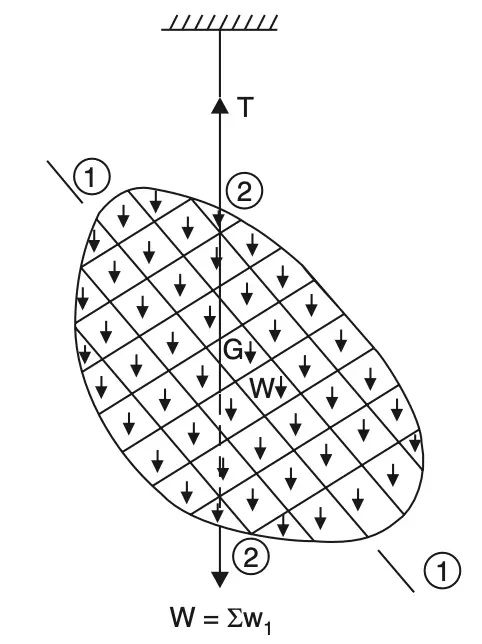
Let the line of action of the resultant weight be 2–2 intersecting 1–1 at G. It is obvious that if the body is suspended in any other position, the line of action of resultant weight W passes through G. This point is called the centre of gravity of the body.
Thus the centre of gravity can be defined as the point through which the resultant force of gravity of the body acts.
This method of locating the centre of gravity is a practical method. If one desires to locate the centre of gravity of a body analytically, it is to be noted that the results of the weight of various portions of the body are to be determined.
For this Varignon’s theorem, which states the moment of the resultant force is equal to the sum of moments of component forces, can be used.
Referring to the below figure,
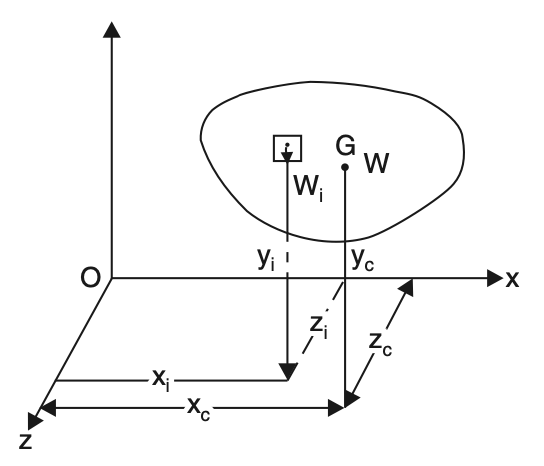
let Wi be the weight of an element in the given body.
W be the total weight of the body.
Let the coordinates of the element be xi, yi , zi and that of centroid G be xc, yc, zc.
Since W is the resultant of Wi forces,
W = W1 + W2 + W3 + . . .
W = ΣWi
and
Wxc = W1x1 + W2x2 + W3x3 + . . .
∴ Wxc = ΣWi xi = ∮ xdw
Similarly,
Wyc = ΣWi yi = ∮ ydw
Wzc = ΣWi zi = ∮zdw
……..Equation A
If M is the mass of the body and mi that of the element, then
M = W/g and mi = Wi/g , hence we get
Mxc = Σmi xi = ∮xi dm
Myc = Σmi yi = ∮yi dm
Mzc = Σmi zi =∮zi dm
……..Equation B
If the body is made up of uniform material of unit weight γ, then we know Wi = Vi γ, where V represents volume, then equation B reduces to
Vxc = ΣVi xi = ∮xdV
Vyc = ΣVi yi = ∮ydV
Vzc = ΣVi zi = ∮zdV
……..Equation C
If the body is a flat plate of uniform thickness as shown in the below figure, in x-y plane,
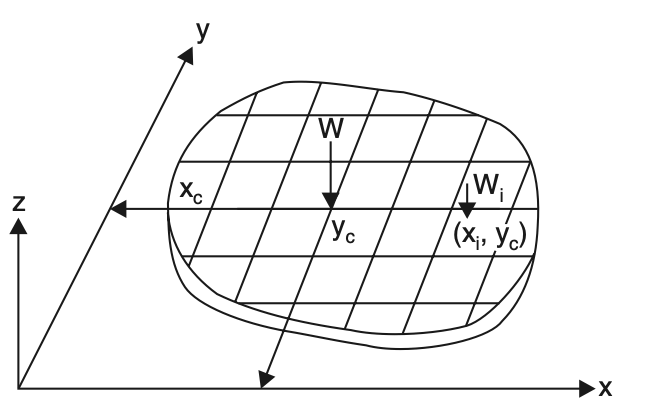
Wi = γ Ai t.
Hence we can rewrite the equation as follows
Axc = ΣAi xi = ∮x dA
Ayc = ΣAi yi = ∮y dA
……..Equation D
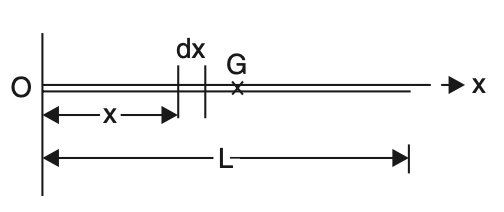
If the body is a wire of uniform cross-section in-plane x, y as shown in the below figure, then we can rewrite the relations as follows
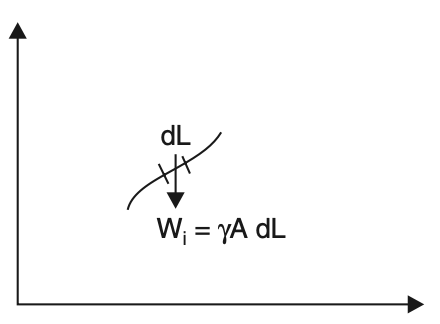
Lxc = Σ Li xi = ∮x dL
Lyc = Σ Li yi = ∮ y dL
……..Equation E
The term centre of gravity is used only when the gravitational forces (weights) are considered. This is the term applicable to solids.
Equation B in which only masses have used the point obtained is termed as the centre of mass.
The central points obtained for volumes, surfaces, and line segments (obtained by Equation C, D, and E) are termed centroids.
Centroid of a Line
The centroid of a line can be determined using equation E.
The method of finding the centroid of a line for some standard cases is illustrated below:
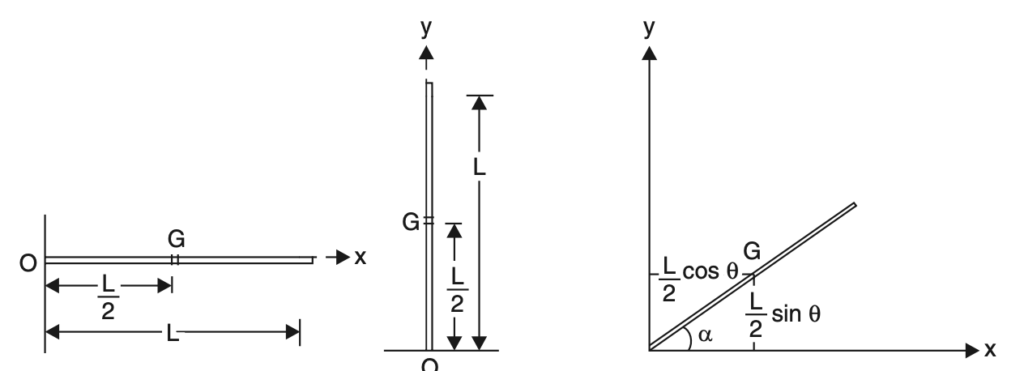
(i) Centroid of a straight line
Selecting the x-coordinate along the line as shown in the below figure.
Lxc = o∫Lx dx
Lxc = [x2/2]Lo
Lxc = L2/2
xc = L/2
Thus the centroid lies at the midpoint of a straight line as shown in the below figure, whatever be the orientation of the line
(ii) Centroid of an Arc of a circle
Referring to below figure
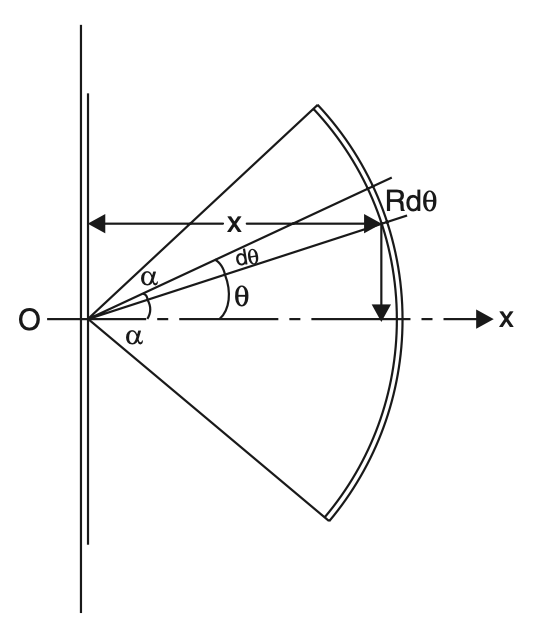
L = Length of arc = R 2α
dL = Rdθ
Hence from equation E
xcL = − -α∫α xdL
xc R 2α = -α∫αR cos θ . Rdθ
xc R 2α = R2[ sinθ]α-α
….. Equation (i)
xc = (R2 × 2sinα)/2Rα
xc = Rsinα/α
and
yc L -α∫α y dL = -α∫α R sin θ . Rdθ
yc L -α∫α y dL = R2 [cos θ]α-α
yc L -α∫α y dL = 0
yc = 0
….. Equation (ii)
From equations (i) and (ii) we can get the centroid of semicircle shown in the below figure by putting α = π/2.
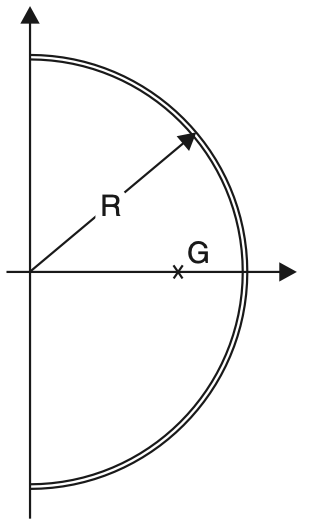
For semicircle xc = 2R/π
yc = 0
For a quarter of a circle shown in the below figure by putting α varying from zero to π/2.
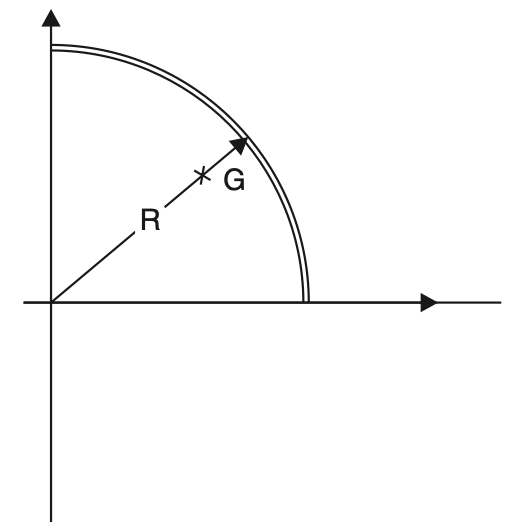
For a quarter of a circle,
xc = 2R/π
yc = 2R/π
(iii) Centroid of composite line segments
The results obtained for standard cases may be used for various segments and then the equations E in the form
xcL = ΣLi xi
ycL = ΣLi yi
The above relations are used used to get centroid xc and yc.
If the line segments are in space the expression zcL = ΣLi zi may also be used.
Let us solve an example problem to find the Centroid of different wire objects.
Example problems to calculate Centroid of wire objects
Problem Statement 1: Determine the centroid of the wire shown in the below figure.
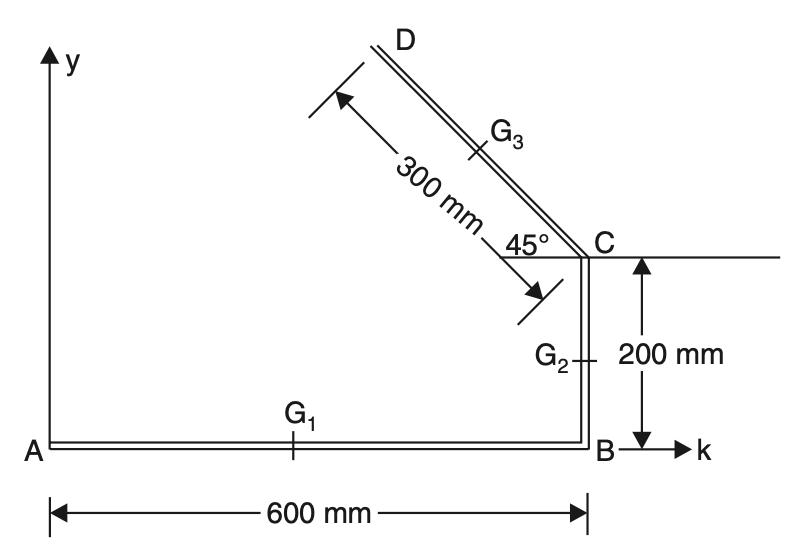
Answer:
The wire is divided into three segments AB, BC, and CD.
Taking A as origin the coordinates of the centroids of AB, BC and CD are
G1(300, 0);
G2(600, 100)
G3 (600 – 150 cos 45°, 200 + 150 sin 45°) = G3 (493.93, 306.07)
L1 = 600 mm,
L2 = 200 mm,
L3 = 300 mm
Total length L = 600 + 200 + 300 = 1100 mm
From the equation Lxc = ΣLi xi , we get
1100 xc = L1x1 + L2x2 + L3x3
1100 xc = (600 × 300) + (200 × 600) + (300 × 493.93)
xc = 407.44 mm
Now, Lyc = ΣLi yi
1100 yc = (600 × 0) + (200 × 100) + (300 × 306.07)
yc = 101.66 mm
Problem Statement 2: Locate the centroid of the uniform wire bent as shown in the given figure below.
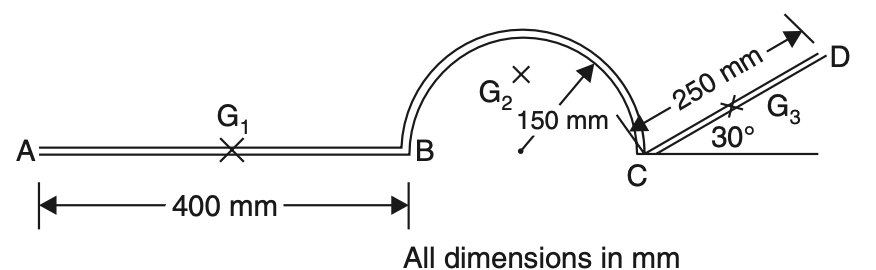
Answer:
The composite figure is divided into three simple figures and taking A as origin coordinates of their centroids noted down as shown below:
AB —a straight line
L1 = 400 mm,
G1 (200, 0)
BC —a semicircle
L2 = 150 π = 471.24,
G2 [475, 2× 150/π] it will be G2 (475, 95.49)
CD —a straight line
L3 = 250;
x3 = 400 + 300 + 250/2 cos 30° = 808.25 mm
y3 = 125 sin 30° = 62.5 mm
Total length L = L1 + L2 + L3 = 1121.24 mm
Lxc = ΣLi xi gives
1121.24 xc = (400 × 200) + (471.24 × 475) + (250 × 808.25)
xc = 451.20 mm
Lyc = ΣLi yi gives
1121.24 yc = (400 × 0) + (471.24 × 95.49) + (250 × 62.5)
yc = 54.07 mm
Problem statement 3: Locate the centroid of uniform wire shown in the figure below.
Note: portion AB is in x-z plane, BC in y-z plane and CD in x-y plane. AB and BC are semi-circular in shape.
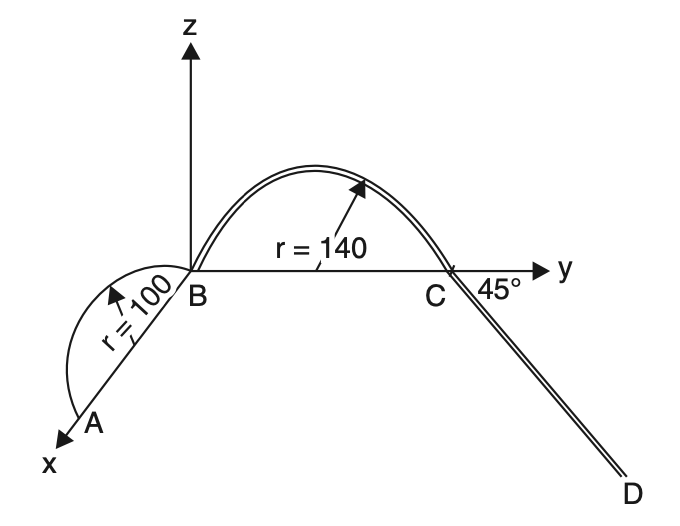
Answer:
The length and the centroid of portions AB, BC, and CD are as shown in the table below:
| Portion | Li | xi | yi | zi |
| AB | 100π | 100 | 0 | (2 × 100)/ π |
| BC | 140π | 0 | 140 | (2 × 140)/ π |
| CD | 300 | 300 sin 45° | 280 + 300 cos 45° = 492.13 | 0 |
L = 100π + 140π + 300 = 1053.98 mm
From equation Lxc = ΣLi xi , we get
1053.98 xc = 100π × 100 + 140π × 0 + 300 × 300 sin 45°
xc = 90.19 mm
Similarly,
1053.98 yc = (100π × 0) + (140π × 140) + (300 × 492.13)
yc = 198.50 mm
1053.98 zc = (100π × 200/π) + (140π × 2/140/π) + (300 × 0)
zc = 56.17 mm
First Moment Of Area And Centroid
We know from the equation A
xc = (Wi xi) / W
yc = (Wi yi)/ W
zc = (Wi zi) / W
From the above equation, we can make the statement that the distance of the centre of gravity of a body from an axis is obtained by dividing the moment of the gravitational forces acting on the body, about the axis, by the total weight of the body.
Similarly from equation D, we have,
xc = Ai xi /A
yc = Ai yi /A
By terming ΣAi x: as the moment of area about the axis, we can say the centroid of the plane area from any axis is equal to the moment of area about the axis divided by the total area.
The moment of area ΣAi x: is termed as the first moment of the area also just to differentiate this from the term ΣAi xi 2, which will be dealt with later.
It may be noted that since the moment of area about an axis divided by total area gives the distance of the centroid from that axis, the moment of area is zero about any centroidal axis.
Difference between Centroid and Centre of Gravity
From the above discussion, we can draw the following differences between the Centroid and centre of gravity:
- The term centre of gravity applies to bodies with weight, and centroid applies to lines, plane areas, and volumes.
- The Centre of gravity of a body is a point through which the resultant gravitational force (weight) acts for any orientation of the body whereas the centroid is a point in a line plane area volume such that the moment of area about any axis through that point is zero.
Use of Axis of Symmetry
The centroid of an area lies on the axis of symmetry if it exists. This is a useful theorem to locate the centroid of an area.
This theorem can be proved as follows:
Consider the area shown in the below figure. In this figure y-y is the axis of symmetry.
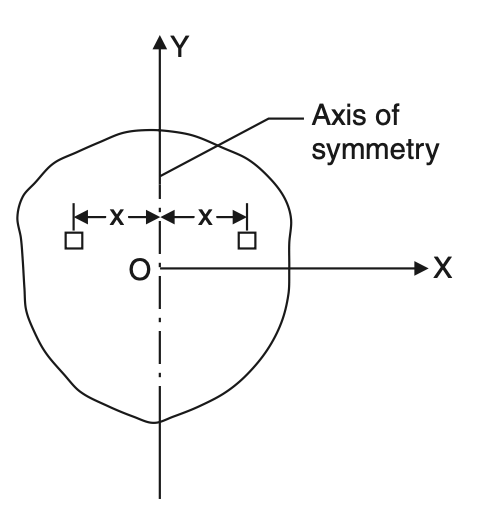
From Equation D, the distance of the centroid from this axis is given by:
(ΣAi xi) / A
Consider the two elemental areas shown in the above figure, which are equal in size and are equidistant from the axis, but on either side.
Now the sum of moments of these areas cancel each other since the areas and distances are the same, but signs of distances are opposite.
Similarly, we can go on considering an area on one side of the symmetric axis and corresponding image area on the other side, and prove that total moments of area (ΣAi xi) about the symmetric axis is zero.
Hence the distance of the centroid from the symmetric axis is zero, i.e., the centroid always lies on the symmetric axis. Making use of the symmetry we can conclude that:
(1) Centroid of a circle is its centre as shown in the below figure
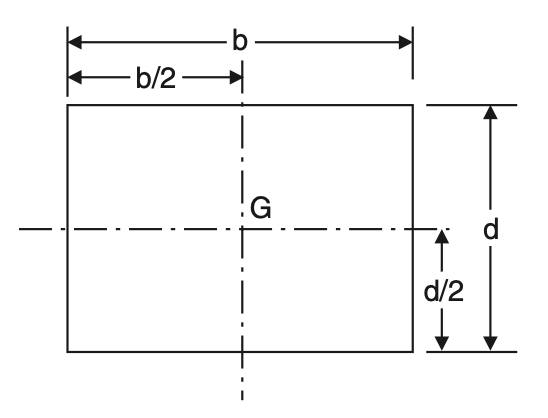
(2) Centroid of a rectangle of sides b and d is a distance b/2 and d/2 from the corner as shown in
the below figure.
Determination of Centroid of Simple Figures From First Principle
For simple figures like triangles and semicircles, we can write a general expression for the elemental area
and its distance from an axis. Then equation D reduces to:
ȳ = (∫ydA)/A
x̅ = (∫xdA)/A
The location of the centroid using the above equations may be considered as finding centroid from the first principle. Now, let us find the centroid of some standard figures from the first principle.
1. Centroid of a Triangle
Consider the triangle ABC of base width b and height as shown in the below figure. Let us locate the distance of the centroid from the base.
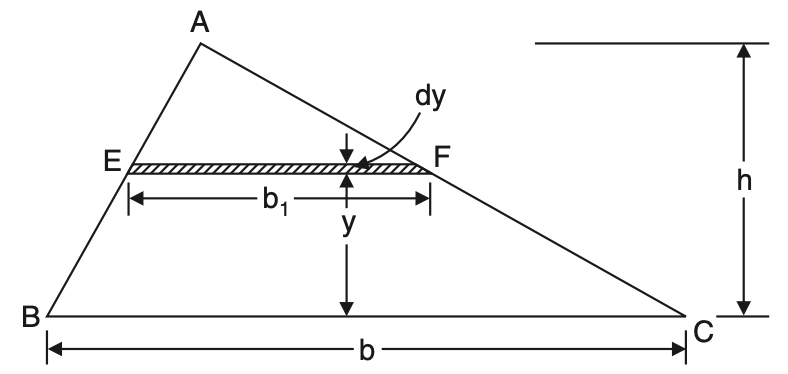
Let b1 be the width of the elemental strip of thickness dy at a distance y from the base. Since AEF and ABC are similar triangles, we can write:
b1/b = (h- y)/ h
b1 =[ (h- y) / h] b
b1 = [1- (y/h)] b
∴ Area of the element
= dA
= b1dy
= [1- (y/h)] b dy
Area of the triangle A = 1/2 bh
From equation D
ȳ = Moment of area/Total area
ȳ = (∫ydA)/A
Now,
∫ ydA = o∫h y [1- (y/h)] b dy
∫ ydA = o∫h [y- (y2/h)] b dy
∫ ydA = b[(y2/2) – (y3/3h)]ho
∫ ydA = (bh2)/6
ȳ = (∫ydA)/A
ȳ = bh2/6 ×1/(1/2bh)
ȳ = h/3
Thus the centroid of a triangle is at a distance of h/3 from the base (or 2h/3 from the apex) of the triangle, where h is the height of the triangle.
2. Centroid of a Semicircle
Consider the semicircle of radius R as shown in the below figure. Due to symmetry centroid must lie on the y-axis.
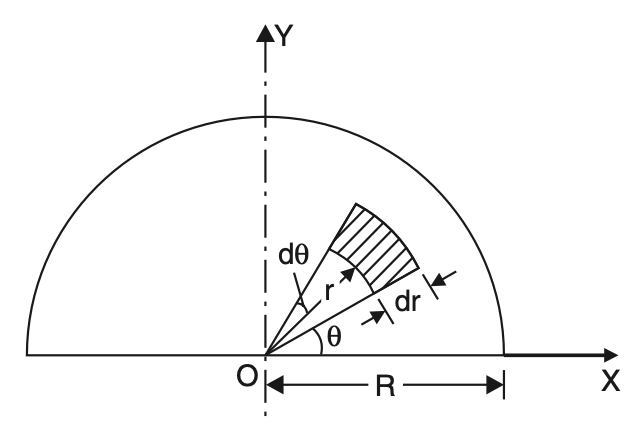
Let its distance from the diametral axis be ȳ.
To find ȳ, consider an element at a distance r from the centre O of the semicircle, radial width being dr and bound by radii at θ and θ + dθ.
Area of element = r dθ dr.
Its moment about diametral axis x is given by:
rdθ × dr × r sin θ = r2sin θ dr dθ
The Total moment of area about the diametral axis,
o∫πo∫R r2 sin θ dr dθ = o∫π[r3/3]Ro sin θ dθ
o∫πo∫R r2 sin θ dr dθ = (R3/3)[-cosθ]πo
o∫πo∫R r2 sin θ dr dθ = (R3/3) [1 + 1]
o∫πo∫R r2 sin θ dr dθ = 2R3/3
Area of semicircle A = 1/2 = πR2
ȳ = Moment of area /Total area
ȳ = (2R3/3) / (1/2πR2)
ȳ = 4R/3π
Thus, the centroid of the circle is at a distance of 4R/3π from the diametral axis.
3. Centroid of Sector of a Circle
Consider the sector of a circle of angle 2α as shown in the below figure. Due to symmetry, the centroid lies on the x-axis.
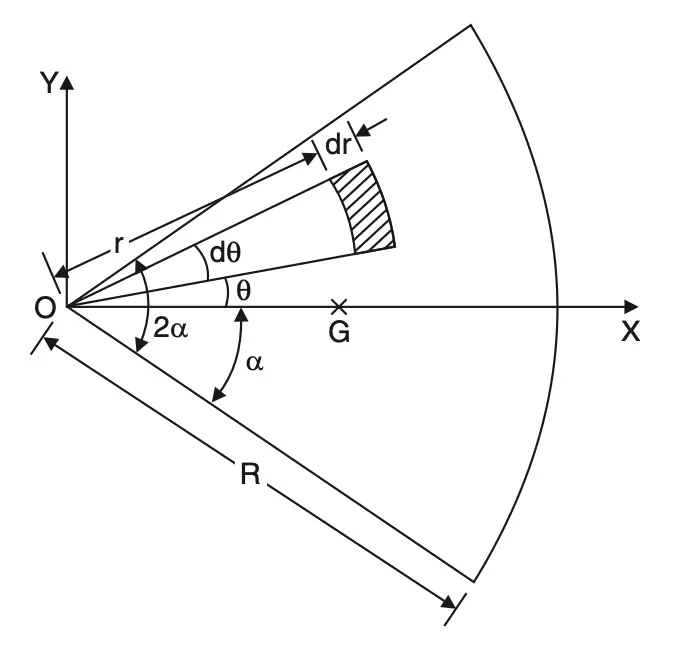
To find its distance from the centre O, consider the elemental area shown.
Area of the element =rdθ dr
Its moment about y-axis
= rdθ × dr × r cos θ
= r2cos θ drdθ
Total moment of area about the y-axis
= -α∫αo∫R r2 cos θ drdθ
= [r3/3]Ro [sinθ]α-α
= (R3/3) 2 sin α
The total area of the sector
= -α∫αo∫Rrdrdθ
= -α∫α[R2/2]dθ
= (R2/2) [θ]α-α
= R2α
The distance of the centroid from center O = Moment of the area about y-axis / Area of the figure
= [(2R3/3) sinα] / R2α
= [2R/3α] sinα
The distance of the centroid from centre O is [2R/3α] sinα.
4. Centroid of Parabolic Spandrel
Consider the parabolic spandrel shown in the below figure.
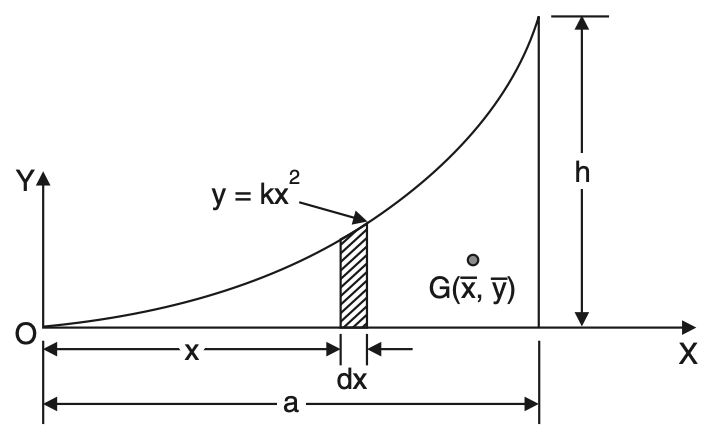
Height of the element at a distance x from O is
y = kx2
Width of element = dx
Area of the element = kx2 dx
Total area of spandrel is
= o∫akx2dx
= [kx3/3]ao
= ka3/3
Moment of area about y axis
= o∫a kx3 dx
= [kx4/4]ao
= kx4/4
Moment of area about x axis
= o∫a dA y/2
= o∫a kx2 dx (kx2/2)
= o∫a(k2x4/2)dx
= k2a2/10
x̅ = (kx4/4) ÷ (kx3/3)
x̅ = 3a/4
ȳ = k2a5+ka3/3
ȳ = (3/10)ka2
From the above figure, at x = a, y = h
∴ h = ka2 or k =h/a2
ȳ = (3/10) × (h/a2) a2
∴ ȳ = 3h/10
Thus, centroid of spandrel is [3a/4 3h/10]
Centroid of Commonly used Geometries
Following are some of the commonly used geometries.
1. Triangle
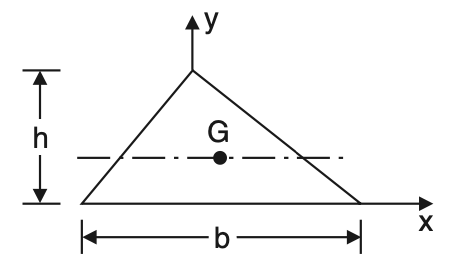
x̅ = –
ȳ = h/3
Area = bh/3
2. SemiCircle
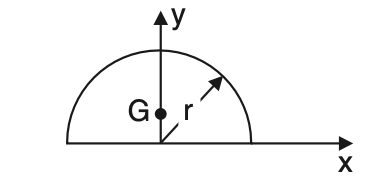
x̅ = 0
ȳ = 4R/3π
Area = πR2/2
3. Quarter circle
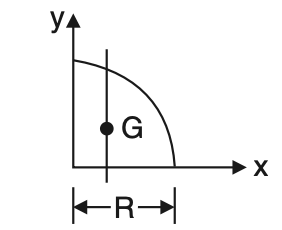
x̅ = 4R/3π
ȳ = 4R/3π
Area = πR2/4
4. Sector of a circle
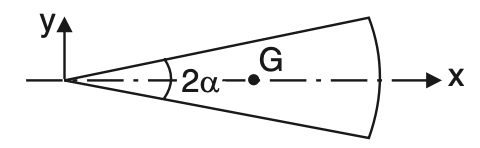
x̅ = (2R/3α) sin a
ȳ = 0
Area = α R2
5. Parabola
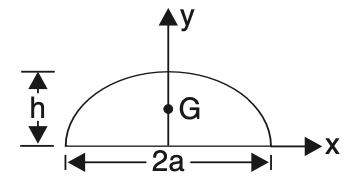
x̅ = 0
ȳ = 3h/5
Area = 4ah/3
6. Semi Parabola
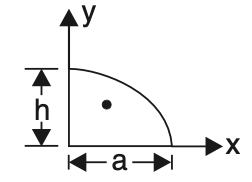
x̅ = 3a/8
ȳ = 3h/5
Area = 2ah/3
7. Parabolic spandrel
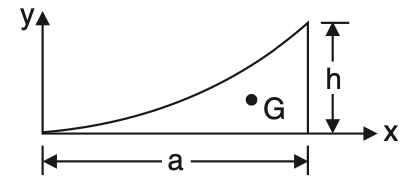
x̅ = 3a/4
ȳ = 3h/10
Area = ah/3
Determination of Centroid of Composite Sections
So far, the discussion was confined to locating the centroid of simple figures like rectangle, triangle, circle, semicircle, etc. In engineering practice, the use of sections that are built up of many simple sections is very common. Such sections may be called built-up sections or composite sections.
To locate the centroid of composite sections, one need not go for the first principle (method of integration). The given composite section can be split into suitable simple figures and then the centroid of each simple figure can be found by inspection or using the standard formulae listed in the above table. Assuming the area of the simple figure is concentrated at its centroid, its moment about an axis can be found by multiplying the area with the distance of its centroid from the reference axis. After determining the moment of each area about the reference axis, the distance of the centroid from the axis is obtained by dividing the total moment of the area by the total area of the composite section.
Example problems to calculate Centroid of Composite Sections
Problem Statement 4: Locate the centroid of the T-section shown in the below figure.
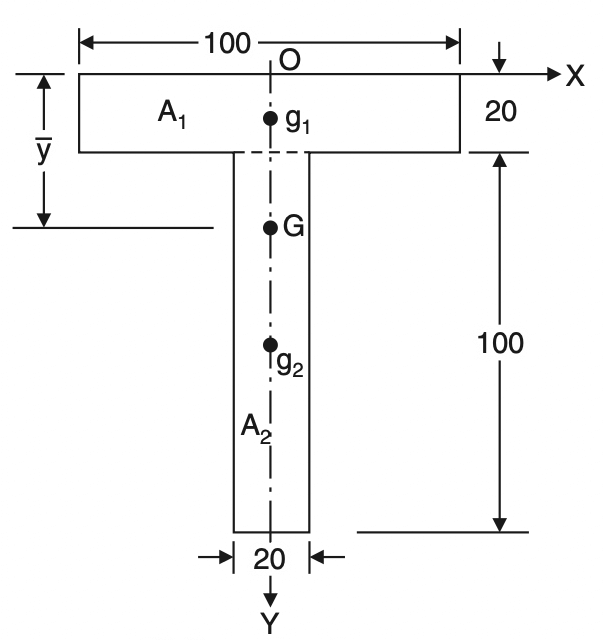
Answer:
Selecting the axis as shown in the above figure, we can say due to symmetry centroid lies on the y-axis which is x = 0.
Now the given T– section may be divided into two rectangles A1 and A2 each of size 100 × 20 and 20 × 100.
The centroid of A1 and A2 are g1(0, 10) and g2(0, 70) respectively.
ȳ = [(100×20×10)+(20×100×70)]/ [100×20)+(20×100)]
ȳ = 40mm
Hence, the centroid of the given T-section is on the symmetric axis at a distance of 40 mm from the top.
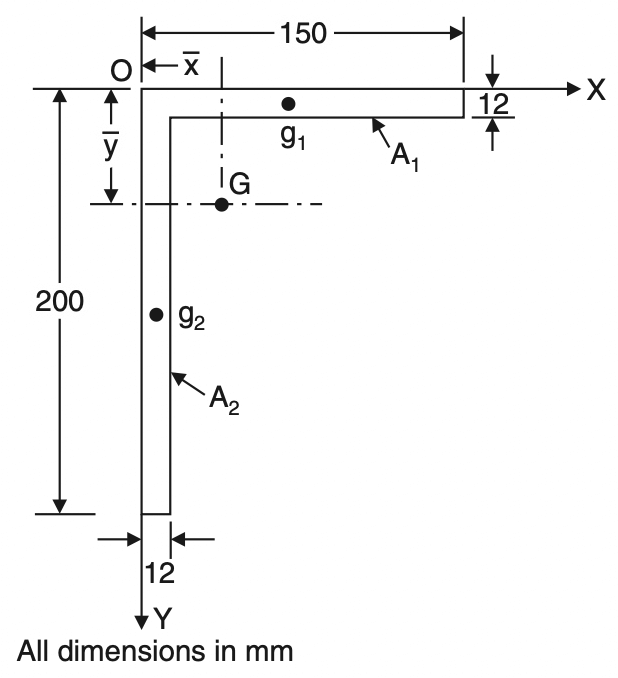
Problem Statement 5: Locate the centroid of the I-section shown in the below figure.
Answer:
Selecting the coordinate system as shown in the above figure, due to symmetry centroid must lie on the y-axis,
x̅ = 0
Now, the composite section may be split into three rectangles
A1 = 100×20 = 2000mm2
The centroid of A1 from the origin is:
y1 = 30 + 100 +(20/2) = 140mm
A2 = 100 × 20 = 2000 mm2
y2 = 30+ (100/2) = 80mm
A3 = 150×30 = 4500mm2
y3 = 30/2 = 15 mm
ȳ = (A1y1+A2y2+A3y3)/A
ȳ = [(2000×140) + (2000×80) + (4500×15)] / [2000 + 2000 + 4500]
ȳ = 59.71mm
Thus, the centroid is on the symmetric axis at a distance of 59.71 mm from the bottom as shown in the above figure.
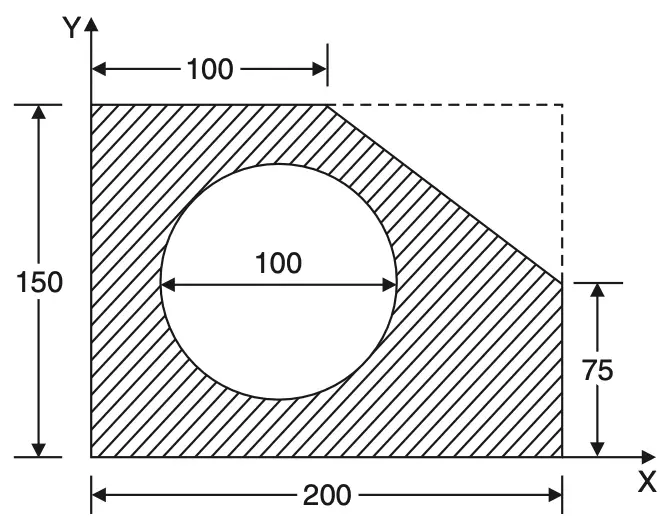
Problem Statement 6: Determine the coordinates xc and yc of the centre of a 100 mm diameter circular hole cut in a thin plate so that this point will be the centroid of the remaining shaded area shown in the below figure (All dimensions are in mm).
Answer:
If xc and yc are the coordinates of the centre of the circle, the centroid also must have the coordinates xc and yc as per the condition laid down in the problem.
The shaded area may be considered as a rectangle of size 200 mm × 150 mm minus a triangle of sides 100 mm × 75 mm and a circle of diameter 100 mm.
The total area will be
Atotal = 200 × 150 – (1/2) × 100 × 75 –[π/4] 1002
Atotal = 18396 mm2
xc = x̅ = {200 × 150 × 100 -(1/2) ×100 × 75 × [200 – (100/3)-(π/4) × 1002 × xc} / 18396
xc(18396) = 200 × 150 × 100 – (1/2) × 100 × 75 × 166.67 – (π/4) × 1002 xc
xc = 2375000/26250
xc = 90.48 mm
Similarly,
18396 yc = 200 × 150 × 75 – 1/2 × 100 × 75 × (150 – 25) – (π/4) × 1002 yc
yc = 1781250.0/26250
yc = 67.86 mm
The Centre of the circle should be located at (90.48, 67.86) so that this point will be the centroid of the remaining shaded area as shown in the above figure.
Note that the centroid of the given figure will coincide with the centroid of the figure without a circular hole. Hence, the centroid of the given figure may be obtained by determining the centroid of the figure without the circular hole also.
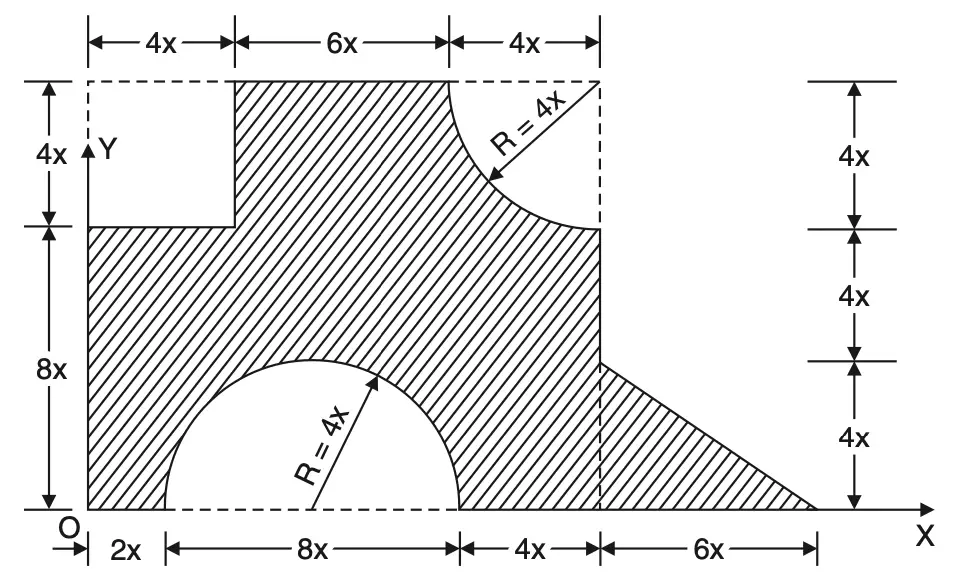
Problem Statement 7: Determine the coordinates of the centroid of the plane are shown in the below figure with reference to the axis shown. Take x = 40 mm.
Answer:
The composite figure is divided into the following simple figures:
(1) A rectangle
A1 = (14x) × (12x) = 168x2
x1 = 7x
y1 = 6x
(2) A triangle
A2 = 1/2 (6x) × (4x) = 12x2
x2 = 14x + 2x = 16x
y2 = 4x/3
(3) A rectangle to be subtracted
A3 = (–4x) × (4x) = –16x2
x3 = 2x
y3 = 8x + 2x = 10x
(4) A semicircle to be subtracted
A4 = – 1/2 π (4x)2 = –8πx2
x4 = 6x
y4 = 4R/3π = 4 ×4(x)/3x =16x/3π
(5) A quarter of a circle to be subtracted
A5 = (-1/4) × π (4x)2 = –4πx2
x5 = 14x – (4R/3π) = 14x – (4)[4x/3π] = 12.3023x
y5 = 12x – 4 ×[4x/3π] = 10.3023x
Total area Atotal = 168x2+12x2– 16x2– 8πx2– 4πx2 = 126.3009x2
x̅ = Σ(Aixi) /Atotal
ΣAi xi = 168x2 × (7x + 12x2) × (16x – 16x2) × (2x – 8πx2)× (6x – 4πx2) × 12.3023x
ΣAi xi = 1030.6083x3
x̅ =1030.6083x3/126.3009x2
x̅ = 8.1599x
x̅ = 8.1599 × 40 (∴ since x = 40 mm)
x̅ = 326.40 mm
Similaryly
ȳ = ΣAiyi) /Atotal
Σ Aiyi = 168x2× (6x + 12x2) × [(4x/3) – 16x2] × (10x – 8πx2) × [(16x/3π) – 4πx2] × 10.3023x
Σ Aiyi = 691.8708x3
ȳ = 691.8708x3/126.3009x2
ȳ = 5.4780x
ȳ = 219.12 mm (∴ since x = 40 mm)
Centroid is at (326.40, 219.12).
Conclusion
We have discussed how to calculate the centroid and centre of gravity in a detailed manner. We also discussed the difference between the Centroid and the Center of gravity. We have used 7 example problems to illustrate how to calculate the Centroid and Centre of Gravity. Let us know what do you think in the comment section below.

Leave a Reply