Euler’s Equation of Motion in Fluid Dynamics | Bernoulli’s Equation

In the previous article, we discussed the velocity and acceleration at a point in a fluid flow, without taking into consideration the forces causing the flow. In this article, we will study the behaviour of fluid flow due to the forces exerted by gravity and pressure with help of the Euler’s Equation of Motion.

Equation of Motion of Fluid Flow

To study the dynamics of fluid flow by considering the forces causing the flow by analysing Newton’s second law of motion, which relates the acceleration with the forces. The fluid is assumed to be incompressible and non-viscous.

According to Newton’s second law of motion, the net force ‘F_x‘ acting on a fluid element in the direction of ‘x’ is equal to the mass ‘m’ of the fluid element multiplied by the acceleration ‘a_x‘ in the x-direction.

Thus mathematically,

F_x = m × a_x

….. Equation (a)

In the fluid flow, There are different forces present, those were mentioned below.

• F_g = gravity force.
• F_p = the pressure force
• F_v = force due to viscosity
• F_t = force due to turbulence
• F_c = force due to compressibility

Thus in equation (a), the net force

F_x = (F_g)_x + (F_p)_x + (F_v)_x + (F_t)_x + (F_c)_x

1. If the force due to compressibility, F_c is negligible, the resulting net force
   F_x = (F_g)_x + (F_p)_x + (F_v)_x + (F_t)_x
   and the equations of motion are called Reynold’s equations of motion.
2. For flow, where (F_t) is negligible, the resulting equations of motion are known as Navier-Stokes Equation.
3. If the flow is assumed to be ideal, viscous force (F_v) is zero and the equation of motions is known as Euler’s equation of motion.

Euler’s Equation of Motion of Fluid Flow

With Euler’s Equation of Motion, the forces due to gravity and pressure are taken into consideration.

This Euler’s Equation of Motion is derived by considering the motion of a fluid element along a streamline.

Let us consider a streamline in which flow is taking place in the s-direction as shown in the following.

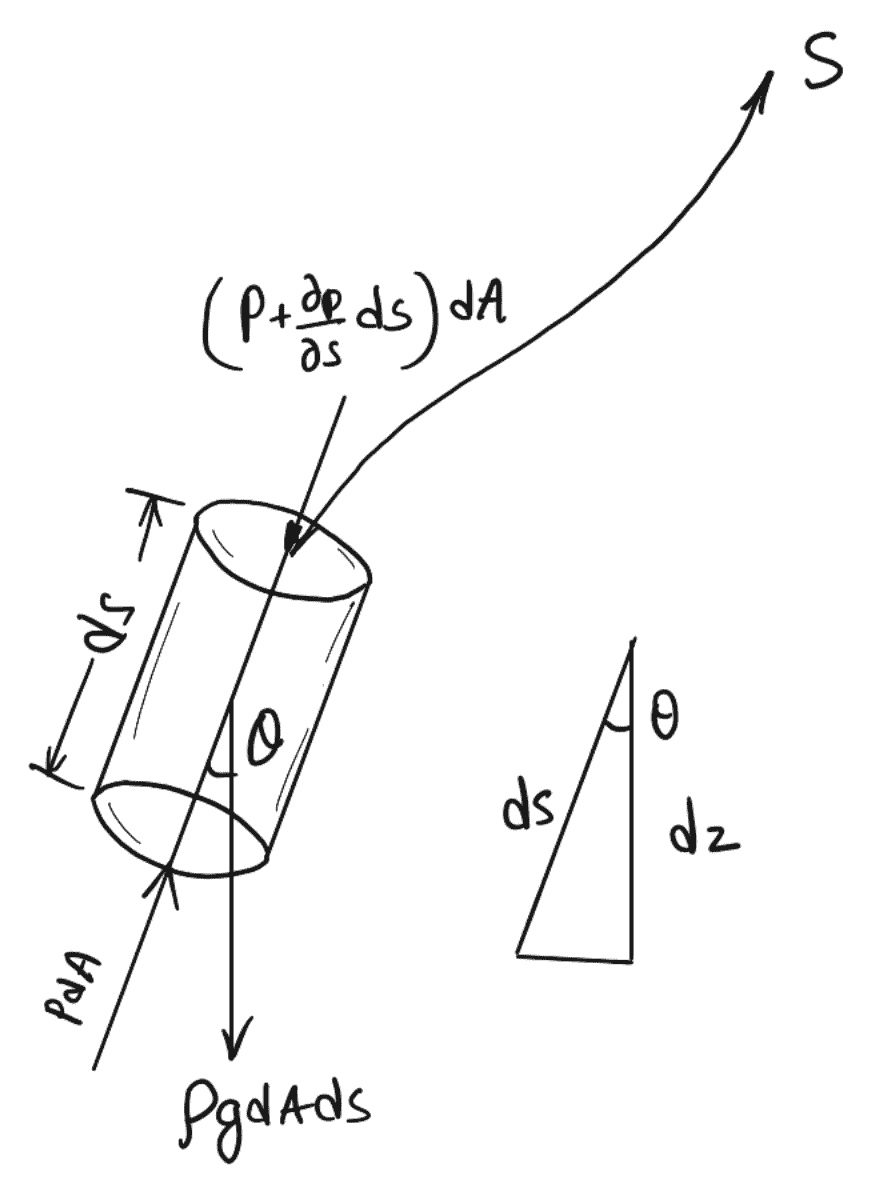
Now consider the cylindrical element of cross-section dA and length ds.

The forces acting on the cylindrical element are as follows.

1. Pressure force, pdA, in the direction of flow.
2. Pressure force, [p + (∂p/∂s) ds] dA opposite to the direction of flow.
3. Weight of the element ρgdAds.

Let θ is the angle between the direction of flow and the line of action of the weight of the element.

The resultant force on the fluid element in the direction of ‘s’ must be equal to the mass of the fluid element × acceleration in the direction s.

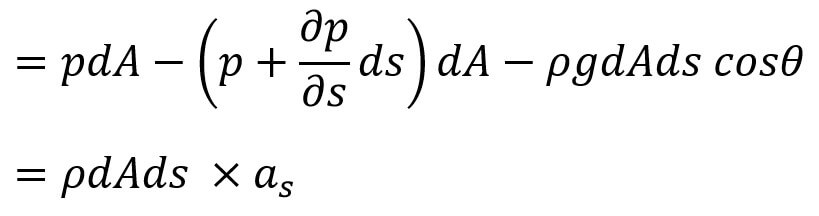
where
a_s = the acceleration in the direction of s.

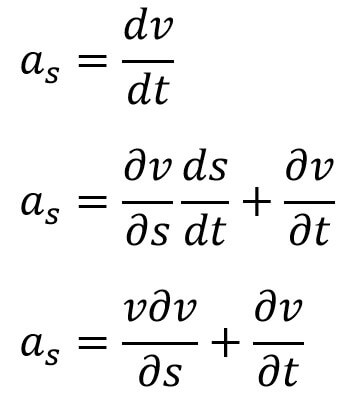
If the Flow is steady then

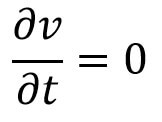
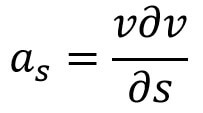
Substituting the value of a_s in equation (b) and simplifying, we will get

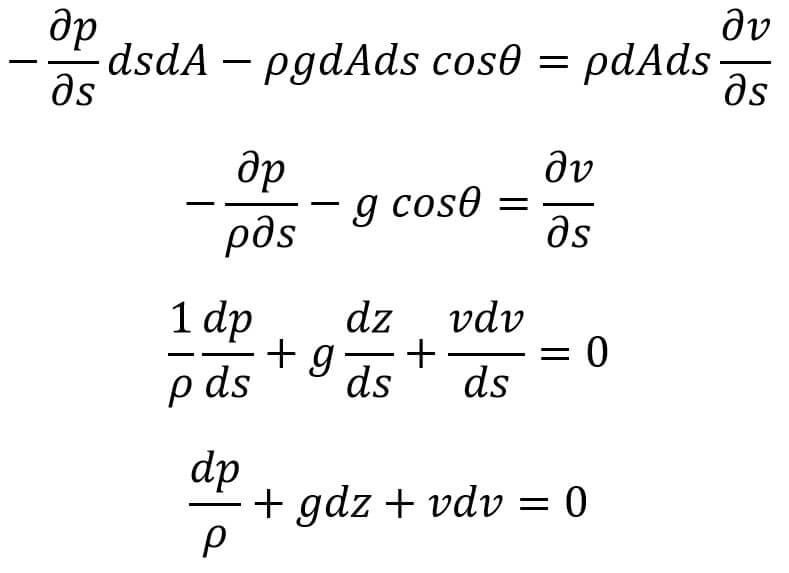
This is the Euler’s Equation of Motion.

Integrating this Euler’s Equation of Motion, we get Bernoulli’s Equation of Motion.

Bernoulli’s Equation of Motion

Bernoulli’s Principle states that as the speed of a moving fluid increases (liquid or gas), the pressure within the fluid decreases.

Bernoulli’s equation can be obtained by integrating Euler’s equation of motion (c),

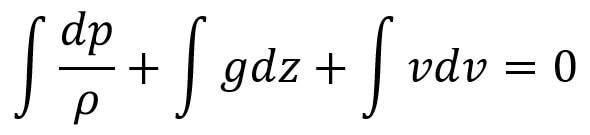
If the flow is incompressible, then the ρ is constant and

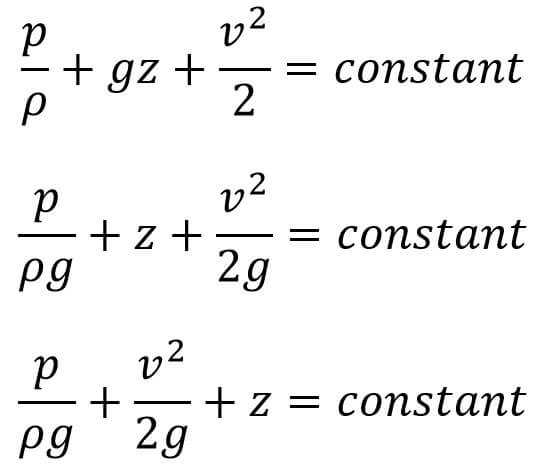
This is the Bernoulli’s Equation of Motion

where
p/ρg = Pressure energy per unit weight of the fluid or pressure head.
v²/2g = kinetic energy per unit weight or kinetic head
z = Potential energy per unit weight or potential head

Assumptions made for Bernoulli’s Equation of Motion

The following are the assumptions made in the derivation of Bernoulli’s equation

(i) The fluid is ideal, (viscosity is zero)
(ii) The flow is steady
(iii) The flow is incompressible
(iv) The flow is irrotational

Bernoulli’s Equation of Motion of a Real Fluid

Bernoulli’s equation was derived on the assumption that fluid is inviscid (non-viscous) and therefore frictionless. But all the real fluids are viscous and hence offer resistance to flow. Thus there are always some losses in fluid flows and hence in the application of Bernoulli’s equation, these losses have to take into consideration.

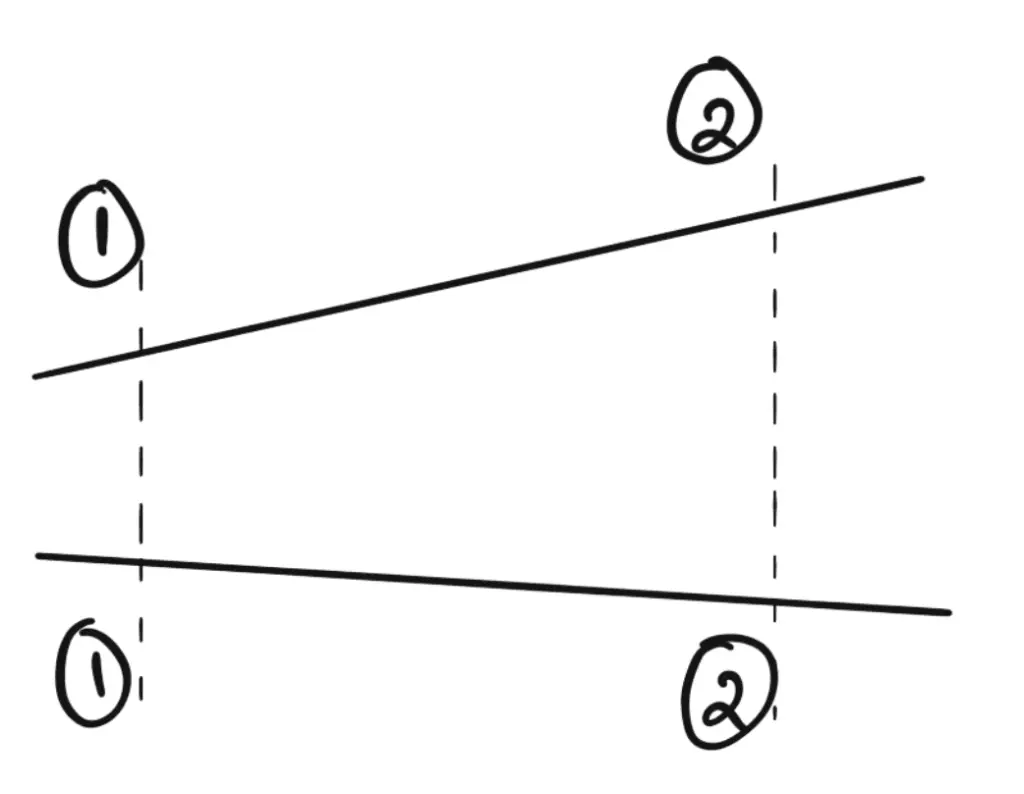
Thus Bernoulli’s equation for real fluids between points 1 and 2 is given by

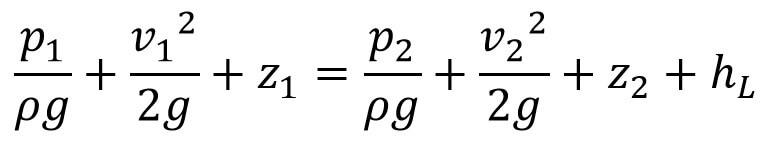
Where h_L is the loss of energy between points 1 and 2

Applications of Bernoulli’s Equation of Motion

Bernoulli’s equation is applied in all problems of incompressible fluid now where energy considerations are involved. But we shall consider its application to the following measuring devices :

1. Venturimeter
2. Orifice meter
3. Pitot-tube

This is all about Bernoulli’s Equation of Motion which is derived from Euler’s Equation of motion. Let us know what you think about this in the comment section below.