How to calculate the Torque required to lift the load by a Screw Jack?

Jackscrew, also known for the screw jack or a worm screw jack, machine screw jack, lead screw jack like many names. This device is used to lift heavy loads with a comparatively smaller effort with a hand lever. It basically converts the rotary motion into linear motion with a screw and nut.

Screw Jack

As we said it used to lift heavy loads by applying relatively less effort with a lever. This mainly consists of a square threaded rod, nut, leaver and thrust collar head. The simple form of a screw jack is shown below.

The square threaded rod is fitted into the nut(which is internally threaded with the same form as the screw rod. and the thrust collar is fitted on the top of the screw rod.

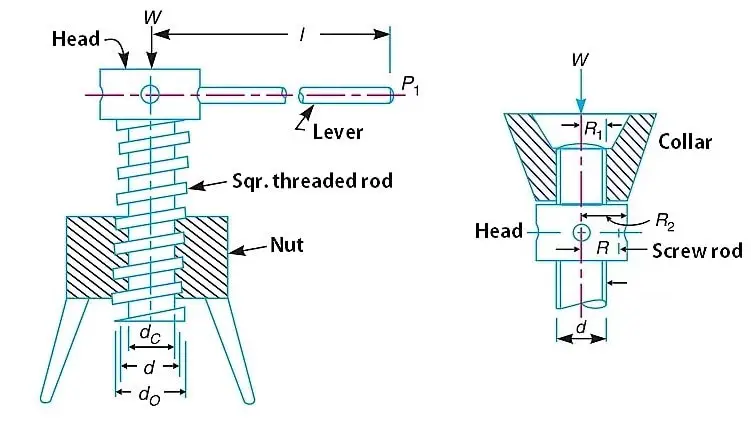
A lever is used to rotate the thrust collar located on the head of the screw rod which will be locked with the screw rod as the collar rotates, the screw rod also rotates in the nut. With one rotation of the collar, it will be lifted by a linear distance same as the pitch of the screw.

The torque required to lift the load by a Screw Jack

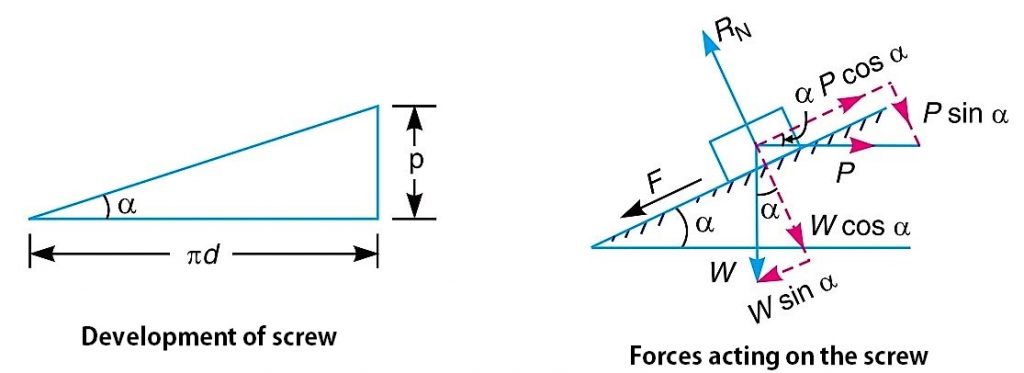
If one complete turn of a screw thread by imagined to be unwound, from the body of the screw and developed, it will form an inclined plane as shown in below figure

• p = Pitch of the screw,
• d = Mean diameter of the screw,
• α = Helix angle,
• P = Effort applied at the circumference of the screw to lift the load,
• W = Load to be lifted, and
• µ = tan φ Coefficient of friction, between the screw and nut (= tan φ), where φ is the friction angle

From the geometry shown above, we can write

tan α = p/π d

Since the principle on which a screw jack works is similar to that of an inclined plane, therefore the force applied on the lever of a screw jack may be considered to be horizontal as shown above figure(right side).

Since the load is being lifted, therefore the force of friction (F = µ.R_N) will act downwards. All the forces acting on the screw are shown in the above figure(right side).

Resolving the forces along the plane,

P cos α = W sin α + F = W sin α + µ.R_N ——–(a)

and resolving the forces perpendicular to the plane,

R_N = P sin α + W cos α ——(b)

Substituting (b) (value of R_N) in equation (a),

P cos α = W sin α + µ (P sin α + W cos α)

P cos α = W sin α + µ P sin α + µ W cos α

P cos α – µ P sin α = W sin α + µ W cos α

P (cos α – µ sin α) = W (sin α + µ cos α)

P = ( W (sin α + µ cos α) )/ (cos α – µ sin α)

Substituting the value of µ = tan φ in the above equation, we get

P = ( W (sin α + tan φ cos α) )/ (cos α – tan φ sin α)

Multiplying the numerator and denominator by cos φ,

P = ( W (sin α cos φ + tan φ cos α cos φ ) )/ (cos α cos φ – tan φ sin α cos φ )

P = ( W (sin α cos φ + sin φ cos α ) )/ (cos α cos φ – sin φ sin α)

P = ( W (sin (α + φ) )/ (cos (α +φ))

P = W tan ( α+φ)

Torque required to overcome friction between the screw and nut

T₁ = P × (d/2)

T₁ = W tan ( α+φ) × (d/2)

When the axial load is taken up by a thrust collar or a flat surface, as shown in above figure, so that the load does not rotate with the screw, then the torque required to overcome friction at the collar,

T₂ = µ₁ × W × (R₁+R₂)/2

T₂ = µ₁ × W × R

• R1 and R2 = Outside and inside radii of the collar
• R = Mean radius of the collar, and
• µ₁ = Coefficient of friction for the collar

∴ Total torque required to overcome friction (i.e. to rotate the screw),

T = T₁ + T₂

T = (P × (d/2)) + (µ₁ × W × R)

If an effort P1 is applied at the end of a lever of arm length l, then the total torque required to overcome friction must be equal to the torque applied at the end of the lever, i.e.

T = P × (d/2) = P₁ × l

Since the mechanical advantage is the ratio of load lifted (W) to the effort applied (P1) at the end of the lever, therefore a mechanical advantage,

M.A.= W/ P₁

M.A.= (W × 2l ) /p.d …( ∴ P₁ = p.d / 2l )

M.A. = (W × 2l )/(W tan ( α+φ) d)

M.A. = 2l / d tan ( α+φ)

When the nominal diameter (d₀) and the core diameter (d_c) of the screw thread is given, then the mean diameter of the screw,

d = (d₀ + d_c)/2

d = d₀-(P/2)

d = d_c -(P/2)

With these equations, we can calculate the torque required to lift the load by a Screw Jack. Following is the example problem for calculating the torque required to overcome friction. Solve it and post the answer in the comments box, I will respond to your comments.

Problem: An electric motor-driven power screw moves a nut in a horizontal plane against a force of 75 kN at a speed of 300 mm/min. The screw has a single square thread of 6 mm pitch on a major diameter of 40 mm. The coefficient of friction at the screw threads is 0.1. Estimate power of the motor.

Note: Use the following formulas to calculate the power of the motor after calculating the Torque.

Power of the motor can be calculated from = Torque × Angular Speed

Angular Speed (ω) = (2 π × N)/60

Conclusion

We have discussed how we can calculate the Torque required to lift the load by a Screw Jack, and also given an example problem for the torque calculation. Solve it, post the answer or comment below, I will post the answer. Or post any doubts, I will answer. Thank you.