In machine Design, each machine member will be mated with another machine member with the defined fit. There are the different type of fits available. They are Clearance Interference, Transition fits. These fits are controlled with some Tolerances and allowances according to some Standards. Actually, these tolerances values can be calculated. According to Indian Standard system of limits and Fits, we have tolerance grades and relative magnitudes, Fundamental deviations. With the help of these, we can calculate the tolerances for the hole or shaft.

To begin with the calculation of hole or shaft tolerances we must understand what is a fundamental deviation.

The fundamental deviation is an allowance rather than tolerance. The allowance is simply the deviation between the hole minimum diameter to the shaft maximum diameter.

See the below the Fundamental deviation chart

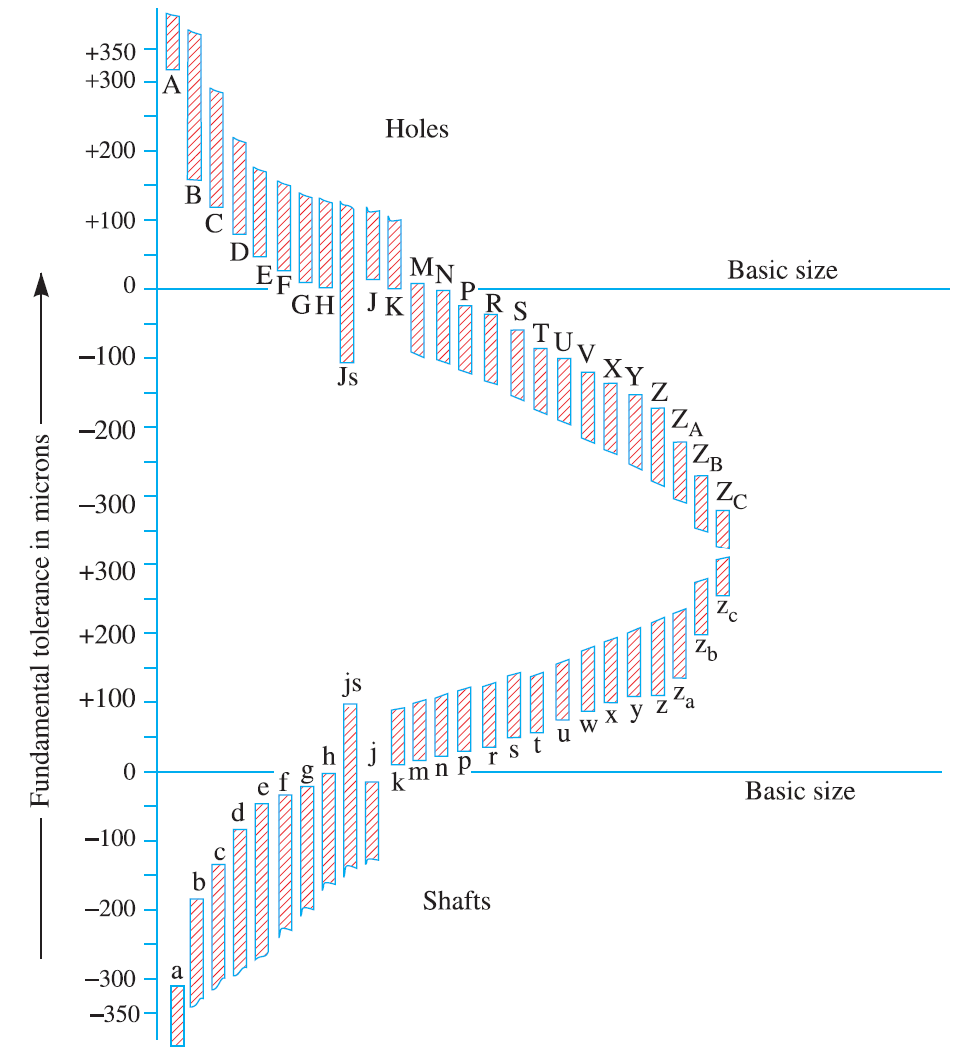
There is a total of 25 fundamental deviations available. All these 25 deviations are represented with the alphabets for holes and shafts. These alphabets are case-sensitive. Block letters are used to represent the hole and small letters are used to represent the shaft deviations. all these deviations are in micrometres(Microns)

Holes deviations: A, B, C, D, E, F, G, H, JS, J, K, M, N, P, R, S, T, U, W, X, Y, Z, Z_A, Z_B, Z_C

Shafts deviations: a, b, c, d, e, f, g, h, js, j, k, m, n, p, r, s, t, u, w, x, y, z, z_a, z_b, z_c

Next, we need to know the International tolerance Grades

International Tolerance Grades

According to Indian standard system of limits and fits, there are total 18 International Tolerance(IT) grades. These grades determine the tolerances for the given designated shaft value. The following are the International tolerance grades.

IT01, IT0, IT1, IT2, IT3, IT4, IT5, IT6, IT7, IT8, IT9, IT10, IT11, IT12, IT13, IT14, IT15, IT16.

But how we will use this tolerance grades?

Here is how we use these grades.

IT01 to IT4 – For the production of gauges, plug gauges, measuring instruments
IT5 to IT 7 – For fits in precision engineering applications
IT8 to IT11 – For General Engineering
IT12 to IT14 – For Sheet metal working or press working
IT15 to IT16 – For processes like casting, general cutting work

Where

 (Units in Microns, 1Micron = 0.001)

D = Geometric mean diameter in mm

(Tolerances for the grades IT2, IT3, IT4 are scaled approximately)

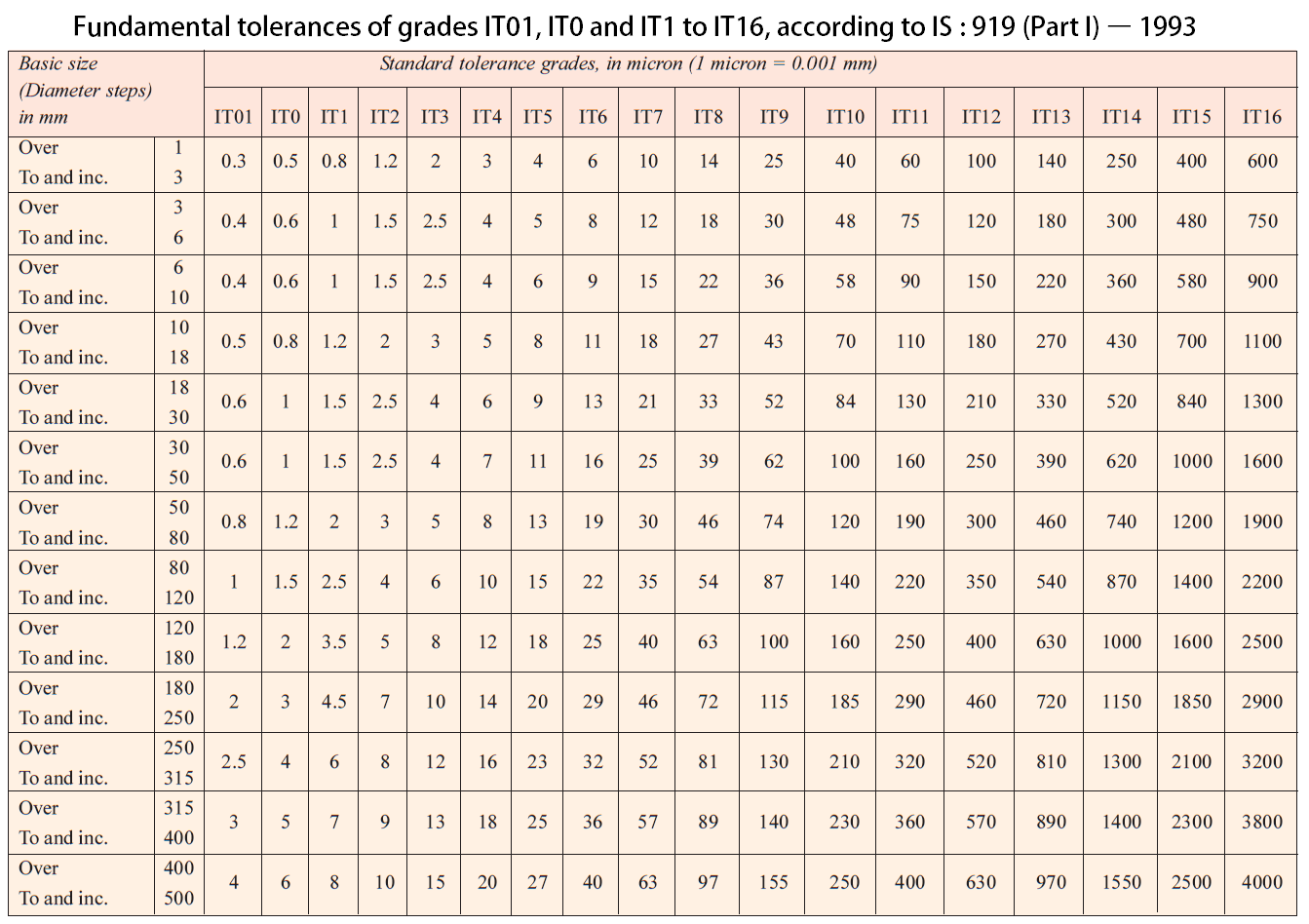
These tolerance values are calculated and listed in the following table For all 18 grades according to the diameter steps range from 1 to 500mm

Now we have an idea what is a fundamental deviation and a tolerance right? Let’s go to next

For example, If a shaft designated as 40H8/f7 it represents that 40mm id=s the basic size and the tolerance grade for the hole is 8(IT8) with a deviation H and the tolerance for the shaft is 7 (IT7) with the shaft deviation of f

Let’s see how we can calculate Tolerances and the Fundamental deviations for the Hole or a Shaft.

Procedure to Calculate tolerance values for shaft or a hole

1. Calculating Fundamental Deviation

a) Calculation of Fundamental Deviation for Shafts

The upper deviation and the lower deviation for the shafts are represented as es, ei

IT may be noted that the shafts from a to h, the upper deviation are considered, whereas the shafts j to z_c, The lower deviation will be considered.

ei = es – IT     (or)   es = ei +IT

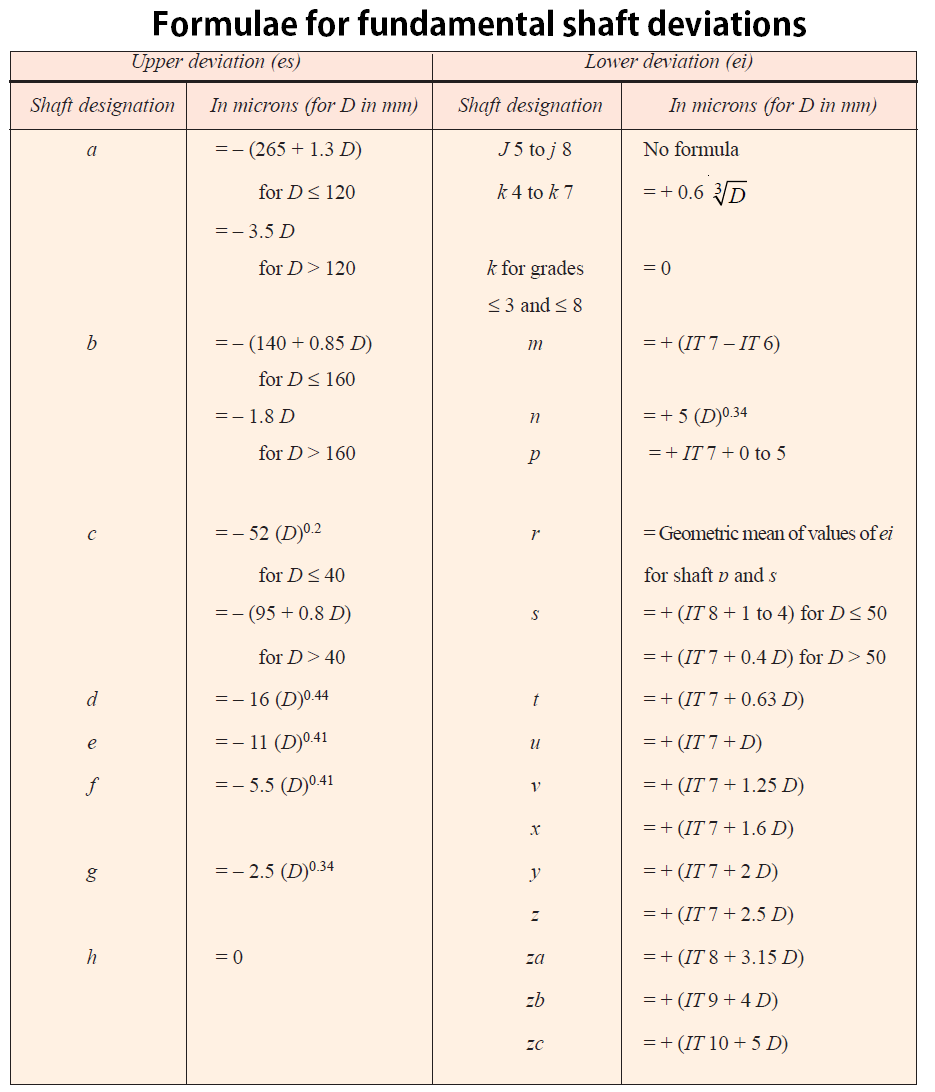
Exception: For js the shaft (Upper and lower) deviation is ±IT/2

with these formulas, the deviation can be calculated

where

D = Geometric mean diameter in mm

it will be taken from the below table

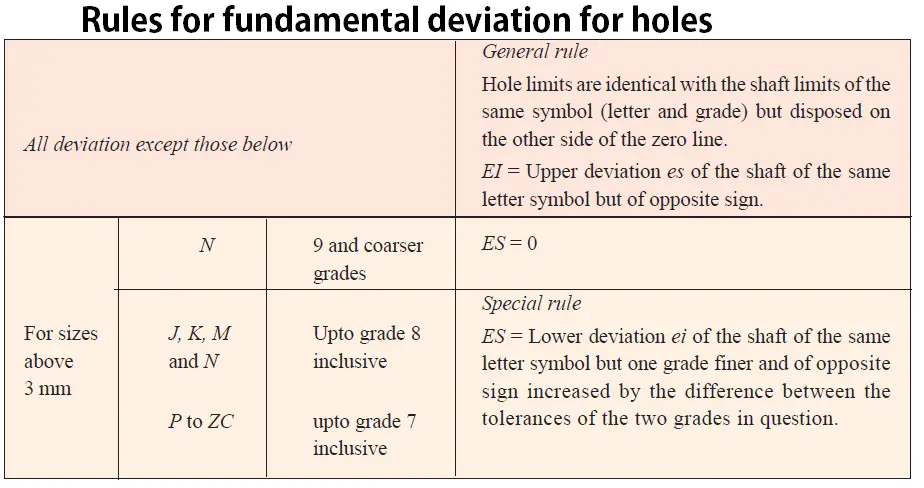
b) Calculation of Fundamental Deviation for Holes

The upper deviation and the lower deviation for the Hole are represented with EI, ES

EI = ES – IT    (or) ES = EI + IT

See the below tabular for calculating the Deviation for the holes

Example Problem to Calculate tolerance values for shaft or a hole

Problem: Calculate the tolerances, Fundamental Deviations and limits of sizes for the shaft designated as 40H8/f7.

Solution:

A Shaft designation is given as 40H8/f7

40 is lies between the diameters 30and 50 (These values are taken from the standard Tables [Table: 1])

D = √(30×50) = 38.73

From above equation i = 0.00156  (1 micron = 0.001mm)

The relevant magnitude for the grade IT8 = 25i = 25 x 0.00156 = 0.039   …………………….i

The relevant magnitude for the grade IT7 = 16i = 16 x 0.00156 = 0.025    ……………………ii

[These values can be directly taken from the Table 1 ]

Fundamental Deviation

The fundamental Lower deviation for the hole always will be (EI) = 0   ……………. iii

Fro the Table: 2

The fundamental deviation (Upper deviation) for the shaft f

es = -5.5 (D)^0.41

es = -5.5 (38.73)^0.41 

es = -24.63 microns (25 microns) = -0.025mm ……………….iv

The fundamental deviation (lower deviation) for the shaft f

ei = es – IT

ei = -0.025-0.025 = -0.050  ………………………v     ( where IT7 = 0.025 from above)

This negative sign indicates the fundamental deviation lies below the zero line

Limits of Sizes

From above the lower deviation for the hole is (EI) = 0

The lower limit will be 40.000

The upper limit for the hole = Lower limit for hole + Tolerance value for the hole

The upper limit for the hole =  40.000+0.039 = 40.039

The hole Limits will be 40.000/40.039

The upper limit for the shaft = Lower limit for the hole(Basic Size) – Fundamental Deviation

The upper limit for the shaft = 40.000-0.025 = 39.975

The lower Limit for the shaft =  Upper limit for the shaft – Tolerance For shaft

The lower Limit for the shaft = 39.975-0.025 = 39.950

The shaft limits will be 39.975/39.950

Conclusion

This is a quick calculation procedure to calculate the tolerance for the designated shaft or holes. [Reference Machine Design by RS kurmi]