How to Calculate the Force Exerted by Jet on Stationary Objects?

A Nozzle is the portion of the pipe where the cross-sectional area varies from larger diameter to smaller diameter, and it can be used to direct or modify the flow of a fluid. A jet is a liquid stream projected into a surrounding medium or an object from the nozzle. In this article, we will discuss the force exerted by Jet on Stationary objects.

The liquid comes out in the form of a jet from the outlet of a nozzle, which is fitted to a pipe through which the liquid is flowing under pressure. If some plate, which may be fixed or moving, is placed in the path of the jet, a force is exerted by the jet on the plate. This force is obtained from Newton’s second law of motion or from the impulse-momentum equation. Thus the impact of a jet means the force exerted by the jet on a plate which may be stationary or moving. Following are the cases of the impact of a jet i.e., the force exerted by the jet on a plate, will be considered

Force exerted by the jet on a stationary plate when

• The plate is vertical to the jet
• The plate is inclined to the jet
• The plate is curved

Force exerted by the jet on a moving plate, when

• The plate is vertical to the jet
• The plate is inclined to the jet
• The plate is curved

Force Exerted by Jet on Stationary Objects

In this article, we will discuss the Force Exerted by Jet on Stationary Objects.

Following are the 3 cases we will discuss how we can calculate the Force Exerted by Jet on Stationary Objects.

1. Force Exerted By the Jet on Stationary Vertical Plate
2. Force Exerted by the Jet on Stationary Inclined Flat Plate
3. Force Exerted by the Jet on Stationary Curved Plate

1. Force Exerted By the Jet on Stationary Vertical Plate

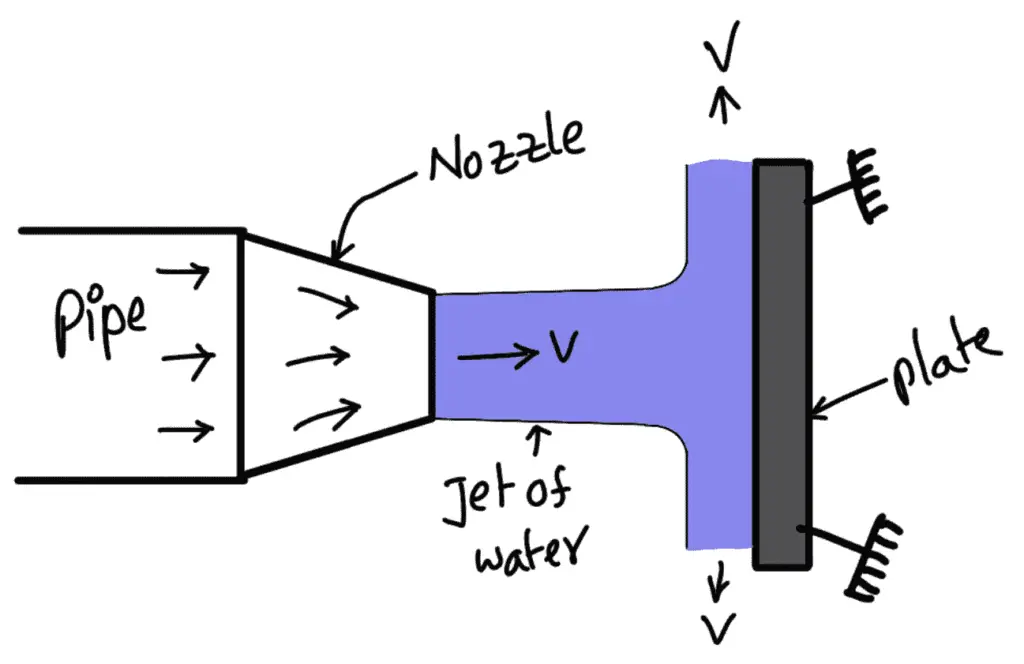
Consider a jet of water coming out from the nozzle, that strikes a flat vertical plate as shown in the following figure

Let
V= velocity of the jet
d = diameter of the jet
a = area of cross-section of the jet = (π/4)d²

The jet after striking the plate will move along the plate. But the plate is at right angles to the jet. Hence the jet after striking will get deflected through 90°. Hence the component of the velocity of the jet, in the direction of the jet, after striking will be zero.

The force exerted by the jet on the plate in the direction of jet,

F_x = Rate of change of momentum in the direction of force

F_x = (Initial momentum – Final momentum) ÷ Time

F_x = (Mass × Initial velocity – Mass × Final velocity) ÷ Time

F_x = Mass × [Initial velocity – Final velocity] ÷ Time

F_x = (Mass/sec) × (velocity of jet before striking – velocity of jet after striking)

F_x = ρaV[V – 0]

F_x = ρaV²

For deriving the above equation, we have taken initial velocity minus final velocity and not final velocity minus initial velocity. If the force exerted on the jet is to be calculated then the final minus initial velocity is taken. But if the force exerted by the jet on the plate is to be calculated, then initial velocity minus final velocity is taken.

For calculating the Force Exerted by Jet on Stationary Object with the above equation, the value of density (ρ) is taken in S.I. units (i.e., kg/m³), and the force (F_x) will be in Newton (N). The value of ρ for water in S.1. units is equal to 1000 kg/m³.

2. Force Exerted by the Jet on Stationary Inclined Flat Plate

Let a jet of water coming out from the nozzle, strikes an inclined flat plate as shown in the following figure.

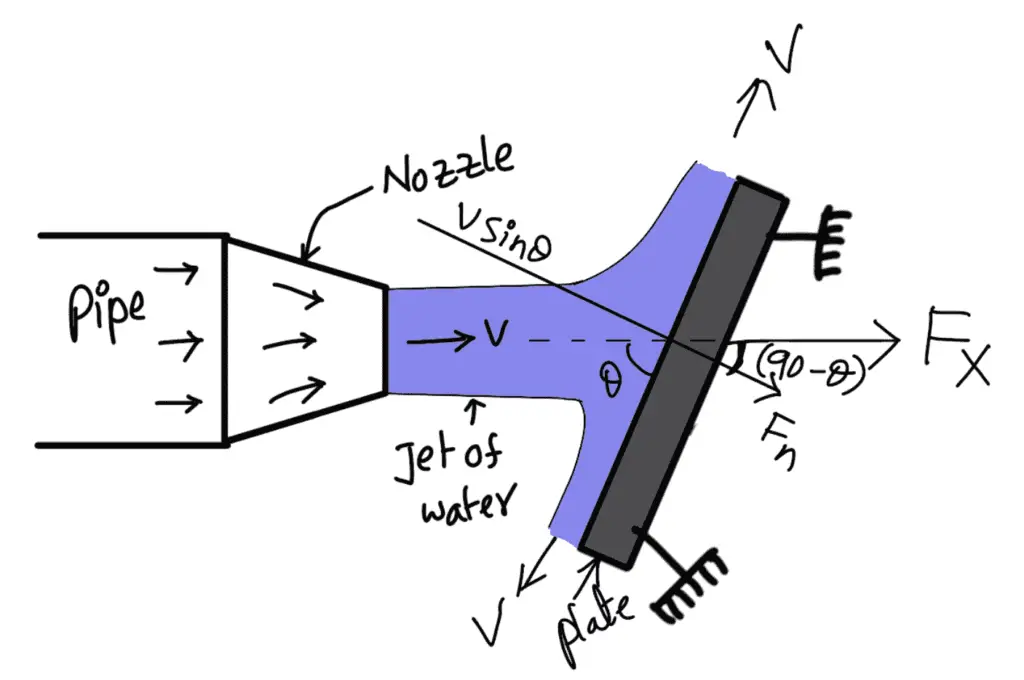
V = Velocity of the jet in the direction of x
θ = Angle between the jet and plate
a = Area of a cross-section of the jet

Then the mass of water per sec striking the plate = ρ x aV

If the plate is smooth and if it is assumed that there is no loss of energy due to the impact of the jet, then the jet will move over the plate after striking with a velocity equal to the initial velocity i.e., with a velocity V.

Let us find the force exerted by the jet on the plate in the direction normal to the plate. Let this force is represented by F_n

F_n = mass of jet striking per second × [ Initial velocity of the jet before striking in the direction of n – Final velocity of jet after striking in the direction of n]

F_n = ρaV [V sin θ – 0 ]

F_n = ρaV² sin θ

This force can be resolved into two components, one in the direction of the jet and another perpendicular to the direction of flow. Then we have,

F_x = component of F_n in the direction of flow
F_x = F_n cos (90° – θ)
F_x = F_n sin θ
F_x = ρAV² sin θ × sin θ
F_x = ρAV² sin² θ

F_y = component of F_n perpendicular to flow
F_y = F_n sin (90° – θ)
F_y = F_n cos θ
F_y = ρAV² sin θ × cos θ

These are the forces exerted by the jet of water in the directions of x and y when the Jet strikes the Stationary Inclined Flat Plate.

3. Force Exerted by a Jet on Stationary Curved Plate

In this third case, we can further derive an expression for the force exerted by a Jet on a Stationary Curved Plate in further 3 more scenarios

• Jet strikes the curved plate at the centre
• Jet strikes the curved plate at one end tangentially when the plate is symmetrical
• Jet strikes the curved plate at one end tangentially when the plate is unsymmetrical

3.1 Jet strikes the curved plate at the centre

Let a jet of water strikes a fixed curved plate at the centre as shown in the following figure.

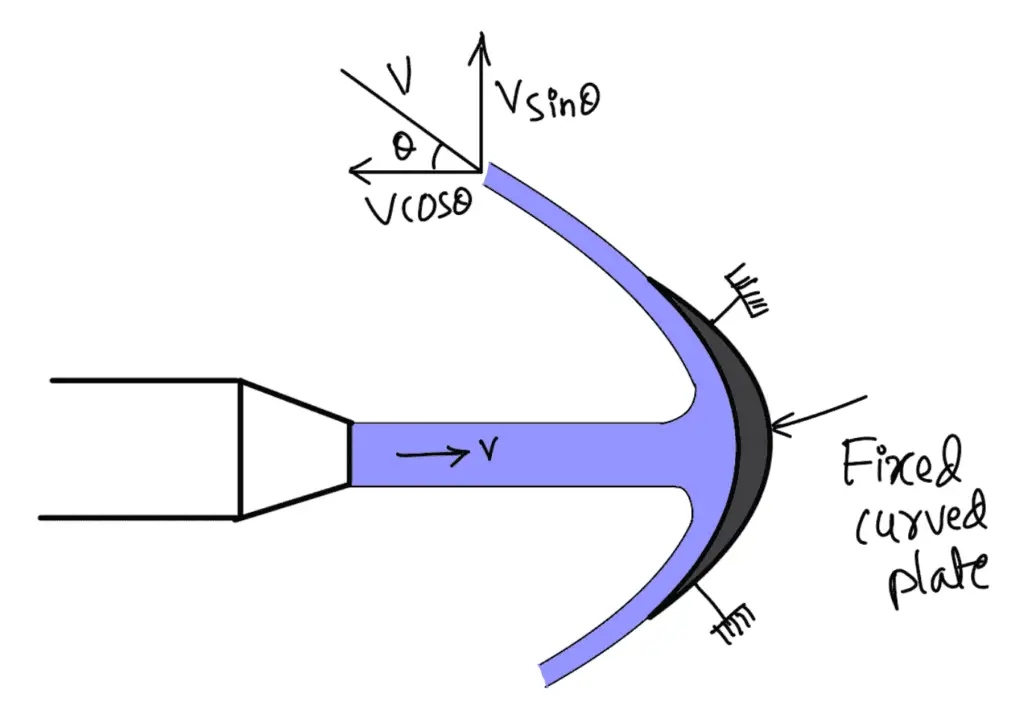
The jet after striking the plate comes out with the same velocity if the plate is smooth and there is no loss of energy due to the impact of the jet, in the tangential direction of the curved plate. The velocity at the outlet of the plate can be resolved into two components, one in the direction of the jet and another perpendicular to the direction of the jet.

Component of velocity in the direction of jet = – V cos θ

(-ve sign is taken as the velocity at the outlet is in the opposite direction of the jet of water coming out from the nozzle).

Force exerted by the jet in the direction of jet F_x = Mass per sec × [V_1x -V_2x]

where
V_1x = Initial velocity in the direction of jet = V
V_2x = Final velocity in the direction of jet = – V cos θ

F_x = ρaV[V – (- V cos θ)]
F_x = ρaV[V + V cos θ]
F_x = ρaV²(1 + cos θ]

F_y = Mass per sec × [V_1y -V_2y]

where
V_1y = Initial velocity in the direction of y = 0
V_2y = Final velocity in the direction of y = V sin θ

F_y = ρaV[0 – V sin θ]
F_y = – ρaV² sin θ

These are the forces exerted by the jet of water in the directions of x and y when the Jet strikes the curved plate at the centre.

-ve sign means that force is acting in the downward direction. In this case the angle of deflection of the jet = (180° – θ)

3.2 Jet strikes the curved plate at one end tangentially when the plate is symmetrical

Let the jet strikes the curved fixed plate at one end tangentially as shown in the following figure.

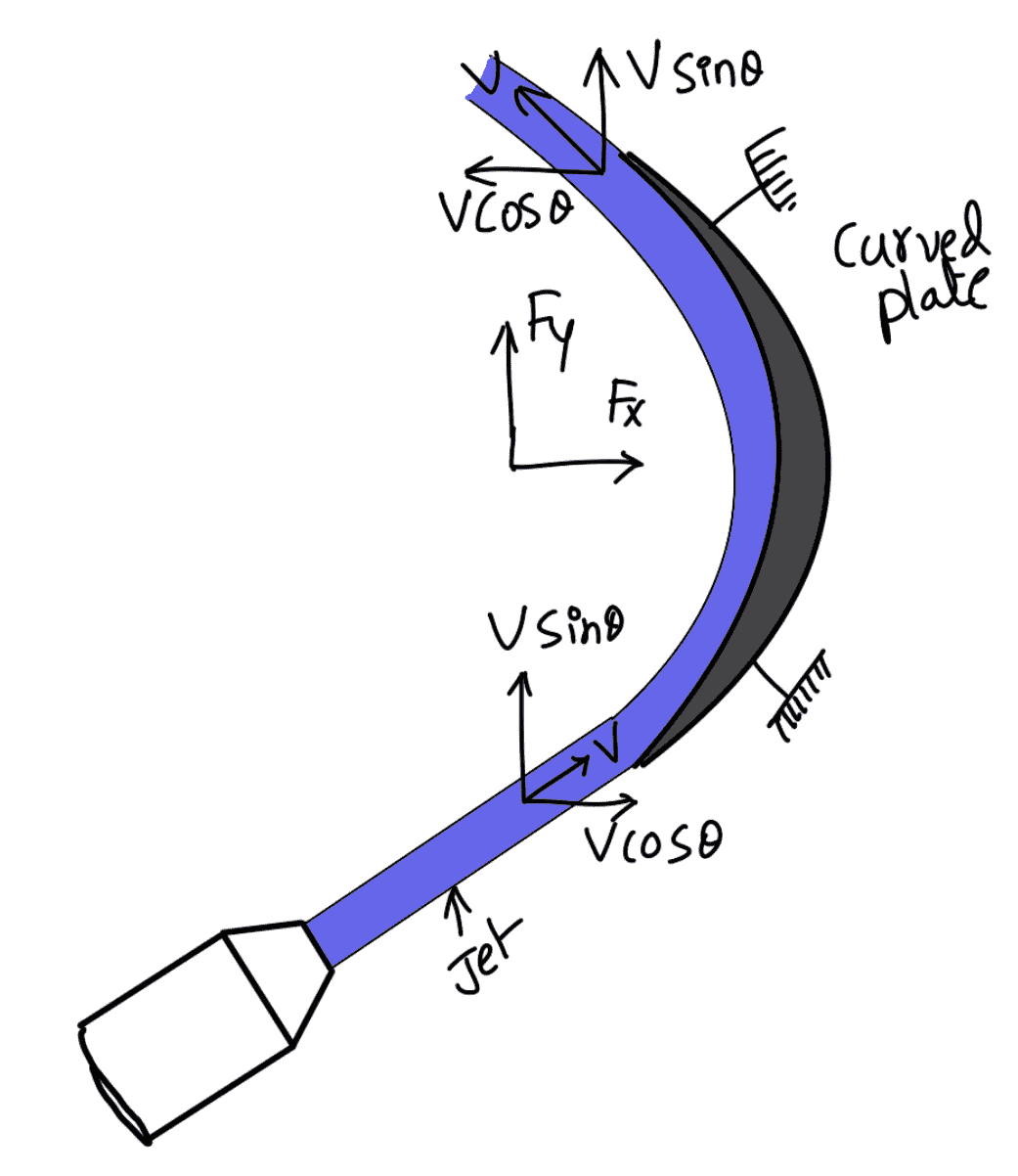
Let the curved plate is symmetrical about the x-axis.

Then the angle made by the tangents at the two ends of the plate will be the same.

Let
V= Velocity of the jet of water,
θ = Angle made by jet with r-axis at inlet tip of the curved plate

If the plate is smooth and the loss of energy due to impact is zero, then the velocity of water at the outlet tip of the curved plate will be equal to V. The forces exerted by the jet of water in the directions of x and y are

F_x = Mass per sec × [V_1x -V_2x]
F_x = ρaV[V cos θ – (- V cos θ)]
F_x = ρaV[V cos θ + V cos θ]
F_x = 2ρaV² cos θ

F_y = ρaV[V_1y -V_2y]
F_y = ρaV[V sin θ – V sin θ ]
F_y = 0

These are the forces exerted by the jet of water in the directions of x and y when Jet strikes the curved plate at one end tangentially when the plate is symmetrical.

3.3 Jet strikes the curved plate at one end tangentially when the plate is unsymmetrical

When the curved plate is unsymmetrical about the x-axis, then the angle made by the tangents drawn at the inlet and outlet tips of the plate with the x-axis will be different.

θ = angle made by tangent at inlet tip with the x-axis,
φ = angle made by tangent at outlet tip with the x-axis

The two components of the velocity at the inlet are

V_1x = V cos θ and V_1y, = V sin θ

The two components of the velocity at the outlet are

V_2x = – V cos φ and V_2y, = V sin φ

The forces exerted by the jet of water in the directions of x and y are

F_x = Mass per sec × [V_1x -V_2x]
F_x = ρaV[V cos θ – (- V cos φ)]
F_x = ρaV[V cos θ + V cos φ]
F_x = ρaV²[cos θ + cos φ]

F_y = Mass per sec × [V_1y -V_2y]
F_y = ρaV[V sin θ – V sin φ]
F_y = ρaV²[sin θ + sin φ]

These are the forces exerted by the jet of water in the directions of x and y when the Jet strikes the curved plate at one end tangentially when the plate is unsymmetrical.

Example Problems to calculate Force Exerted by Jet on Stationary Objects

Problem Statement: Water is flowing through a pipe at the end of which a nozzle is fitted. The diameter of the nozzle is 100 mm and the head of water at the centre nozzle is 100 m. Find the force exerted by the jet of water on a fixed vertical plate. The coefficient of velocity is given as 0.95.

Answer:

Diameter of nozzle d = 100 mm = 0.1 m
Head of water, H = 100 m
Co-efficient of velocity, C_v = 0.95

Also, we know the Density of water (SI units) ρ = 1000 kg/m³

Area of the nozzle, a = (π/4)d² = (π/4)(0.1)² = 0.007854 m²

The theoretical velocity of a jet of water is given as V_th = √(2gH)

V_th = √(2 × 9.81 × 100)
V_th = 44.294 m/s

C_v = Actual velocity / Theoretical velocity

Actual velocity of jet of water, V = C_v × V_th = 0.95 × 44.294 = 42.08 m/s

Force on a fixed vertical plate is given by equation as we discussed above is

F_x = ρaV²
F_x = 1000 × 0.007854 × (42.08)²
F_x = 13907.2 N
F_x = 13.9 kN

A force of 13.9 kN will be exerted by the jet of water on a fixed vertical plate.

Can you solve an example problem by using the above formulas?

Problem Statement: A jet of water of diameter 75 mm moving with a velocity of 25 m/s strikes a fixed plate in such a way that the angle between the jet and plate is 60°. Find the force exerted by the jet on the plate
(i) in the direction normal to the plate
(i) in the direction of the jet.

Solve it and let me know the answer in the comment section below. I will help you get it if you ask any doubt.