Energy Losses in Fluid Flow Through Pipe

With Reynold’s experiment, we have discussed the laminar flow and turbulent flow, and how the transition happens from Laminar to turbulent. In fluid flow, we need to understand and study different energy losses. In this article, we will discuss what are the different major and minor energy losses in a fluid flow.

Energy Losses in Fluid Flow through Pipe

From the previous article, we know when the Reynolds number is less than 2000 for pipe flow, the flow is known as laminar flow whereas when the Reynolds number is more than 4000, the flow is known as turbulent flow.

In order to study and understand different energy losses in fluid flow, we will consider the turbulent flow of fluids through pipes running full will be considered. If the pipes are partially full as in the case of sewer lines, the pressure inside the pipe is the same and equal to atmospheric pressure. Then the flow of fluid in the pipe is not under pressure.

• Major Energy Losses
  • Loss Of Energy (Or Head) Due To Friction
    • Darcy-Weisbach Formula
    • Chezy’s Formula

• Minor Energy Losses
  • Sudden expansion of the pipe
  • Sudden contraction of the pipe
  • Bend in pipe
  • Pipe fittings
  • An obstruction in the pipe

Loss Of Energy (Or Head) Due To Friction

Darcy Weisbach Formula

The loss of head (or energy) in pipes due to friction is calculated from the Darcy Weisbach equation.

Consider a uniform horizontal pipe, having steady flow as shown in the following figure. Let us assume 1-1 and 2-2 are two sections of pipe.

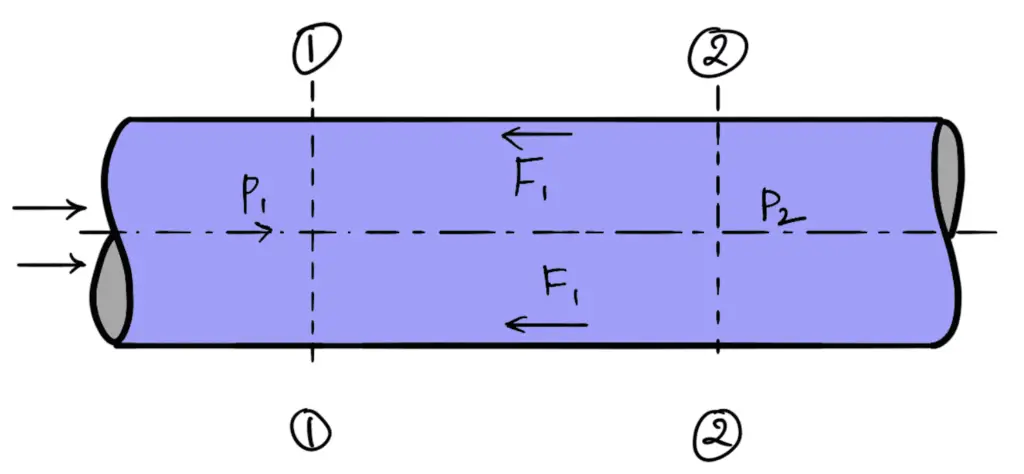
Let
p₁ = pressure intensity at section 1-1
p₂ = pressure intensity at section 2-2
V₁ = velocity of flow at section 1-1
V₂ = velocity of flow at section 2-2
L = length of the pipe between sections 1-1 and 2-2.
d = diameter of pipe
f’= frictional resistance per unit wetted area per unit velocity
h_f = loss of head due to friction

Now, let us apply Bernoulli’s equations between sections 1-1 and 2-2,

Total head at 1-1 = Total head at 2-2 + loss of head due to friction between 1-1 and 2-2

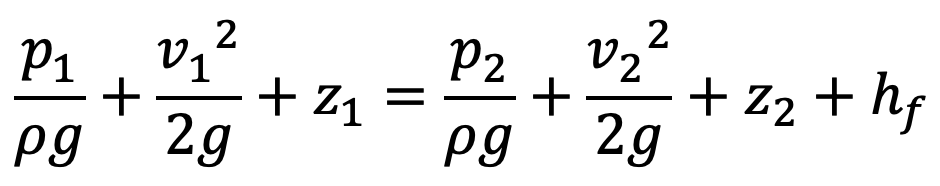
z₁ = z₂ as pipe is horizontal
V₁ = V₂ as the diameter of the pipe is the same at 1-1 and 2-2

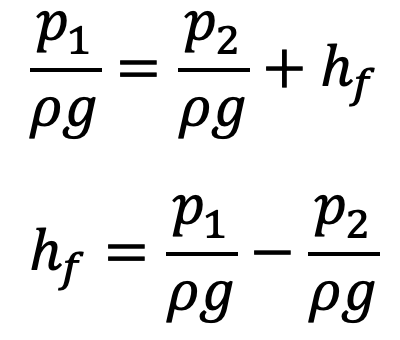
But h_e is the Loss of Energy due to friction and hence the intensity of pressure will be reduced in the direction of flow by frictional resistance.

Frictional resistance = frictional resistance per unit wetted area per unit velocity × wetted area × velocity²
F₁ = f’ × πdL × V²
F₁ = f’ × P × L × V²

The forces acting on the fluid between sections 1-1 and 2-2 are :

1. Pressure force at section 1-1 = p₁ × A ( ∴ where A = Area of pipe)
2. Pressure force at section 2-2 = p₂ × A
3. Frictional force F₁ as shown in the above figure

Resolving all forces in the horizontal direction, we have

p₁ A – p₂ A – F₁ = 0
(p₁ – p₂)A = F₁ = f’ × P × L × V²
p₁ – p₂ = (f’ × P × L × V²) ÷ A

But from above equation (a) equation p₁ – p₂ = ρgh_f

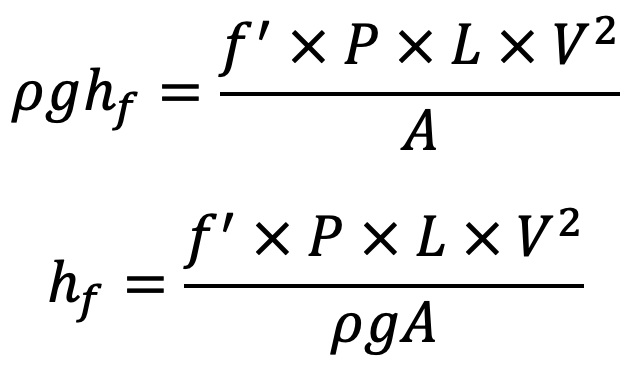
In the above equation, we can put the following

Substituting this in the above equation (b), we get

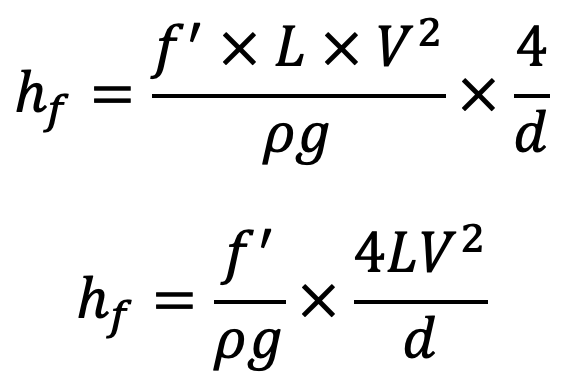
Putting f’/ρ = f/2, we get

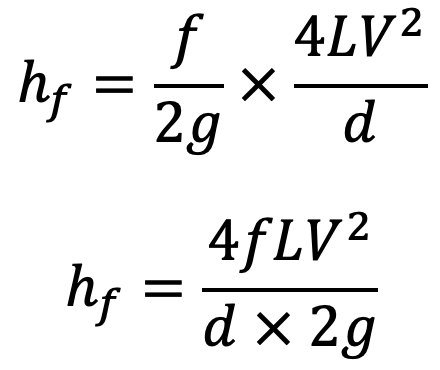
where f is the coefficient of friction

This equation is known as Darcy Weisbach Formula. With help of this equation, we can find out the loss of head due to friction in pipes.

We can also write this equation in the following form.

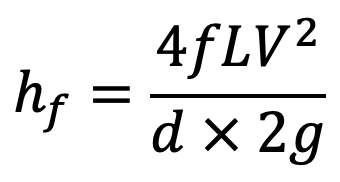
Where
h_f is the loss of head due to friction
f is known as the friction factor or the coefficient of friction which is a function of Reynold’s Number

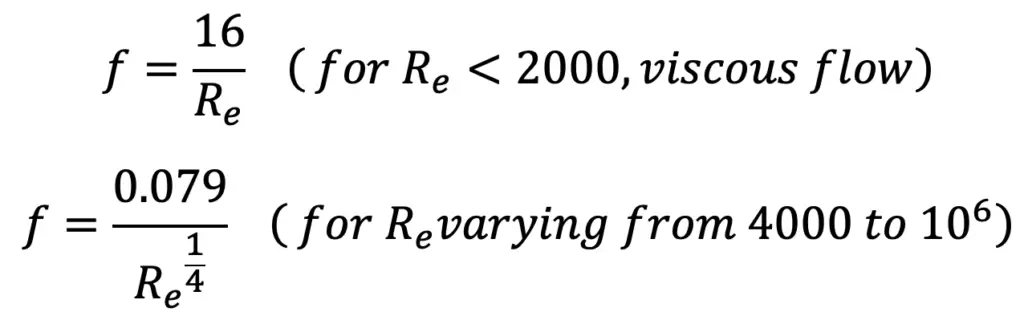
L = length of pipe
V = mean velocity of flow
d = diameter of the pipe

Chezy’s Formula for loss of head due to friction in pipes

We already derived the expression for the loss of head due to friction in pipes which is equation (b)

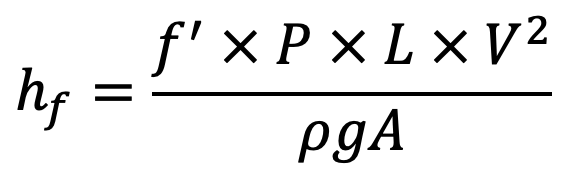
The ratio of the Area of flow to the perimeter (A/P) is called the hydraulic mean depth or hydraulic radius and is denoted by m.

Hydraulic Mean depth m will be

Let us substitute m = A/P = d/4 and P/A = 1/m in the above equation, we get

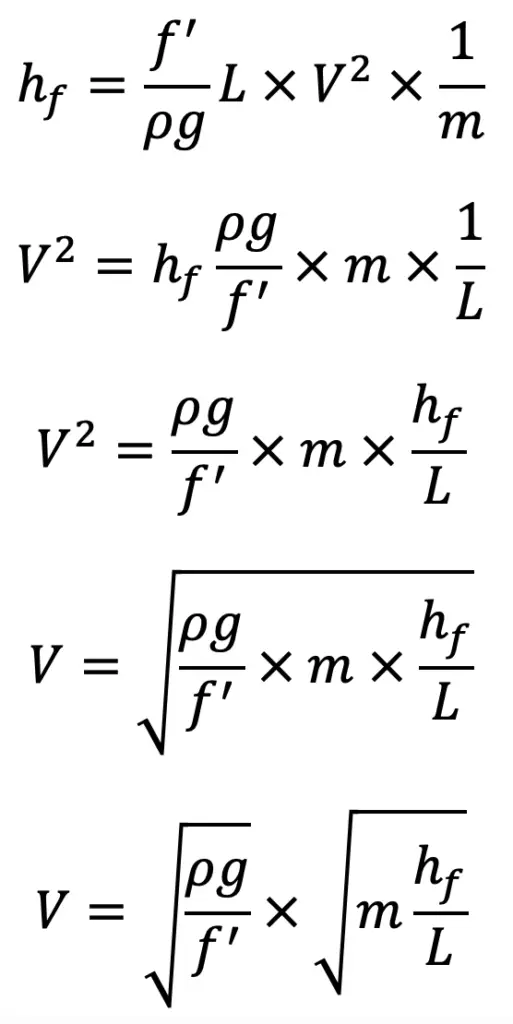
Let us assume

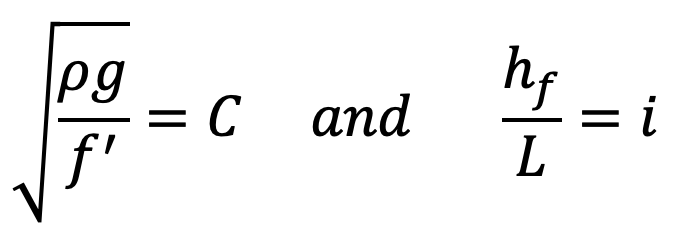
Where
C = a constant known as Chezy’s constant
i = loss of head per unit length of pipe

Let us substitute these into the above equation, we get

V = C √(mi)

…. Equation (d)

Equation (d) is known as Chezy’s formula. Thus the loss of head due to friction in the pipe from Chezy’s formula can be obtained if the velocity of flow through the pipe and also the value of C is known. The value of m for pipe is always equal to d/4.

Example Problem on Energy Losses due to Friction

Let us solve an example problem on the loss of Head or the Energy loss due to the friction in the pipe.

Problem Statement: Find the head lost due to friction in a pipe with a diameter of 300 mm and length of 50 m, through which water is flowing at a velocity of 3 m/s using Darcy formula Chezy’s formula for which C = 60. Take v for water = 0.01 stoke.

Answer:

Given data
Diameter of pipe d = 300 mm = 0.30 m
Length of pipe L = 50 m
Velocity of flow V= 3 m/s
Chezy’s constant C = 60
Kinematic viscosity V = 0.01 stoke = 0.01 cm²/s = 0.01 x 10⁴ m²/s

Energy loss due to friction in pipe by Darcy Formula

Darcy Formula is given by equation (c) as

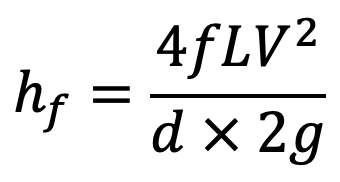
where f = coefficient of friction is a function of Reynolds number, R_e

We know R_e can be calculated from the following relation

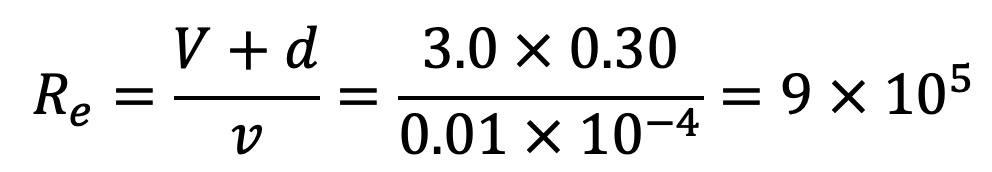
The value of f can be calculated from the following relation

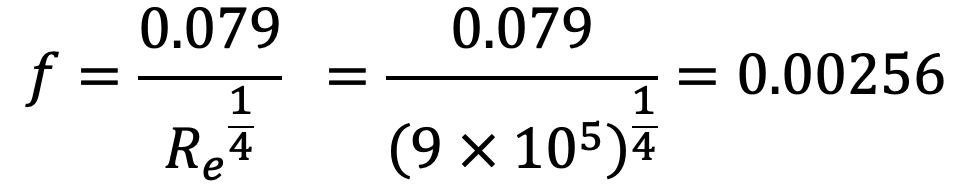
From this, the Loss of Energy due to friction can be calculated as follows

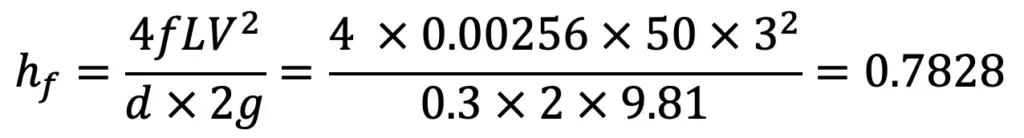
The loss of head due to friction by the using Darcy Formula is 0.7828m

Energy loss due to friction in the pipe by using Chezy’s Formula

Chezy’s Formula is given by equation (d) as

V = C √(mi)

where
C = 60
m = d/4 = 0.30/4 = 0.075m

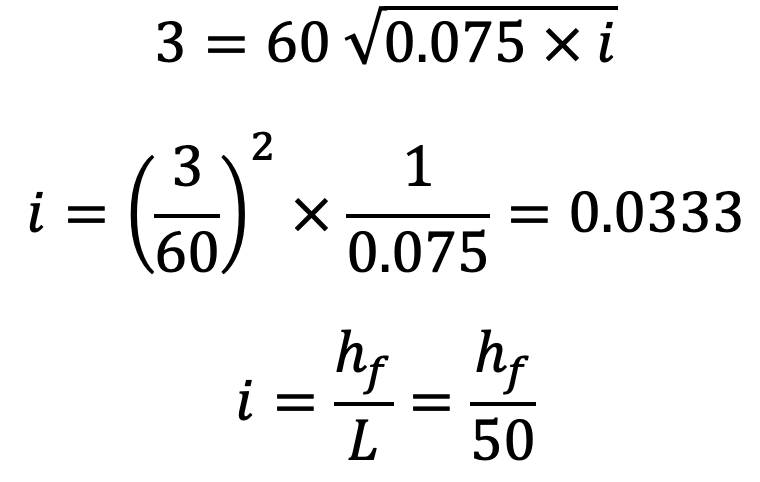
Equating the two values of i, we have

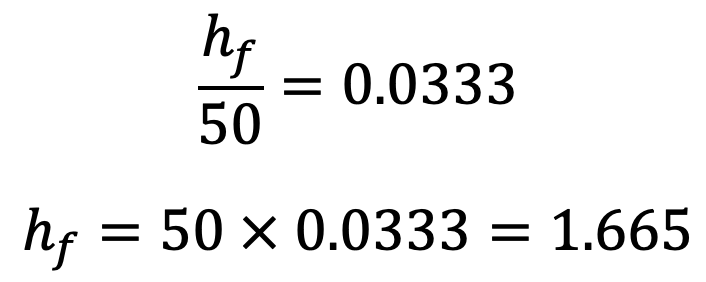
The loss of head due to friction by the using Chezy’s Formula is 1.665m

Minor Energy (Head) Losses

The loss of head or energy due to friction in a pipe is known as a major loss while the loss of energy due to a change of velocity of the following fluid in magnitude or direction is called minor loss of energy. The minor loss of energy (or head) includes the following cases:

1. Loss of head due to sudden enlargement
2. Loss of head due to a sudden contraction
3. Loss of head at the entrance of a pipe
4. Loss of head at the exit of a pipe
5. Loss of head due to an obstruction in a pipe
6. Loss of head due to bending in the pipe
7. Loss of head in various pipe fittings

In the case of a long pipe, the above losses are small as compared with the loss of head due to friction and hence they are called minor losses and even may be neglected without serious error. But in the case of a short pipe, these losses are comparable with the loss of head due to friction.

1. Loss of Head Due To Sudden Enlargement

Consider a liquid flowing through a pipe which has sudden enlargement as shown in the following figure. Consider two sections (1)-(1) and (2)-(2) before and after the enlargement.

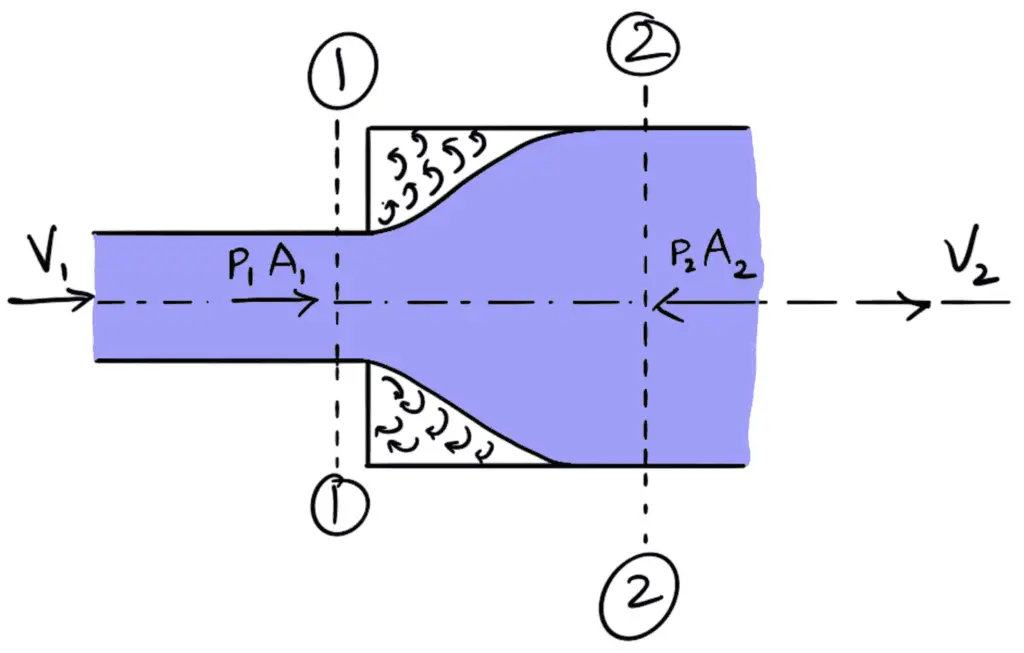
p₁ = pressure intensity at section 1-1
p₂ = pressure intensity at section 2-2
V₁ = velocity of flow at section 1-1
V₂ = velocity of flow at section 2-2
A₁ = Area of pipe at section at 1-1
A₂ = Area of pipe at section at 2-2

Due to the sudden change of diameter of the pipe from D₁ to D₂, the liquid flowing from the smaller pipe is not able to follow the abrupt change of the boundary. Thus the flow separates from the boundary and turbulent eddies are formed as shown in the following figure. The loss of head (or energy) takes place due to the formation of these eddies.

p’ = pressure intensity of the liquid eddies on the area (A₂ – A₁)
h₁ = loss of head due to sudden enlargement

Applying Bernoulli’s equation at sections 1-1 and 2-2,

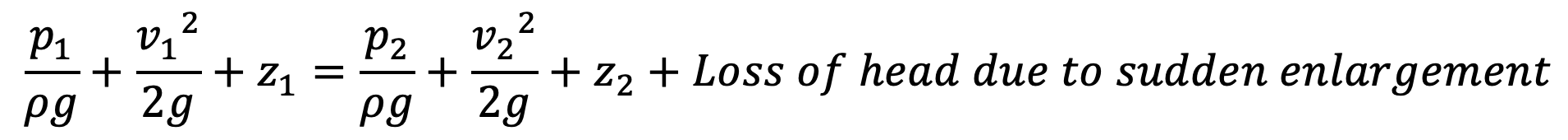
z₁ = z₂ as pipe is horizontal

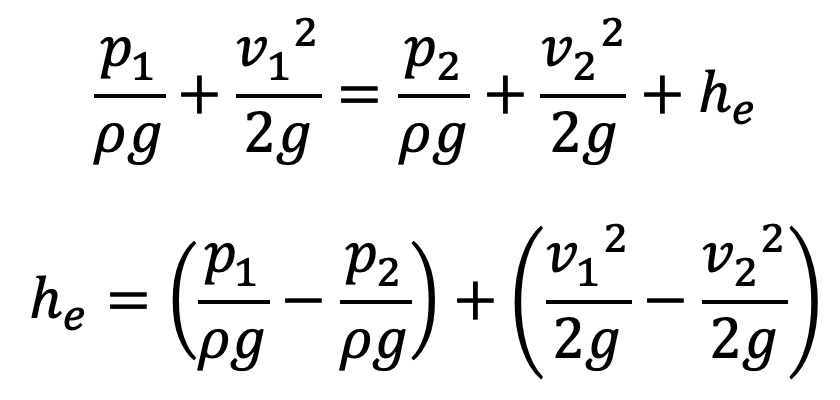
Consider the control volume of liquid between sections 1-1 and 2-2.

Then the force acting on the liquid in the control volume in the direction of flow is given by

F_x = p₁A₁ + p'(A₂ – A₁) – p₂A₂

But experimentally it is found that p’ = p₁

F_x = p₁A₁ + p₁(A₂ – A₁) – p₂A₂
F_x = p₁A₂ – p₂A₂
F_x = (p₁ – p₂)A₂

Momentum of liquid/sec at section 1-1 = mass × velocity

= ρA₁ V₁ × V₁
= ρA₁ V₁²

Momentum of liquid/sec at section 2-2 = mass × velocity

= ρA₂ V₂ × V₂
= ρA₂ V₂²

Change of momentum/sec = ρA₂ V₂² – ρA₁ V₁²

But from continuity equation, we have

A₁V₁ = A₂V₂
A₁ = A₂V₂ ÷ V₁

We can substitute in the above Change of momentum/sec relation, we get

= ρA₂ V₂² – ρA₁ V₁²
= ρA₂ V₂² – ρ × (A₂V₂ ÷ V₁) × V₁²
= ρA₂ V₂² – ρA₂ V₁V₂
= ρA₂ (V₂² – V₁V₂)

Now net force acting on the control volume in the direction of flow must be equal to the rate of change of momentum or change of momentum per second. Hence equating above two equations, we get

(p₁ – p₂)A₂ = ρA₂ (V₂² – V₁V₂)

Rearranging this equation and deviding this with g on both sides, we get

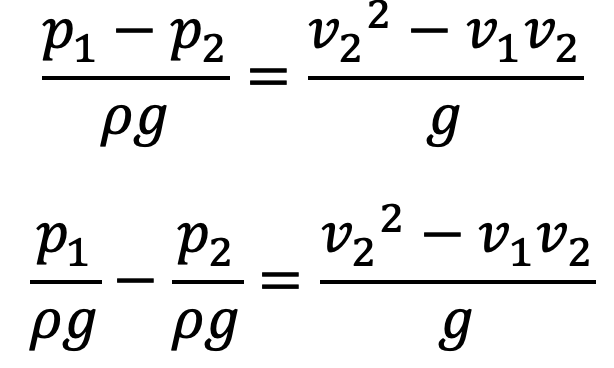
Substituting the value of into the equation (e), we get

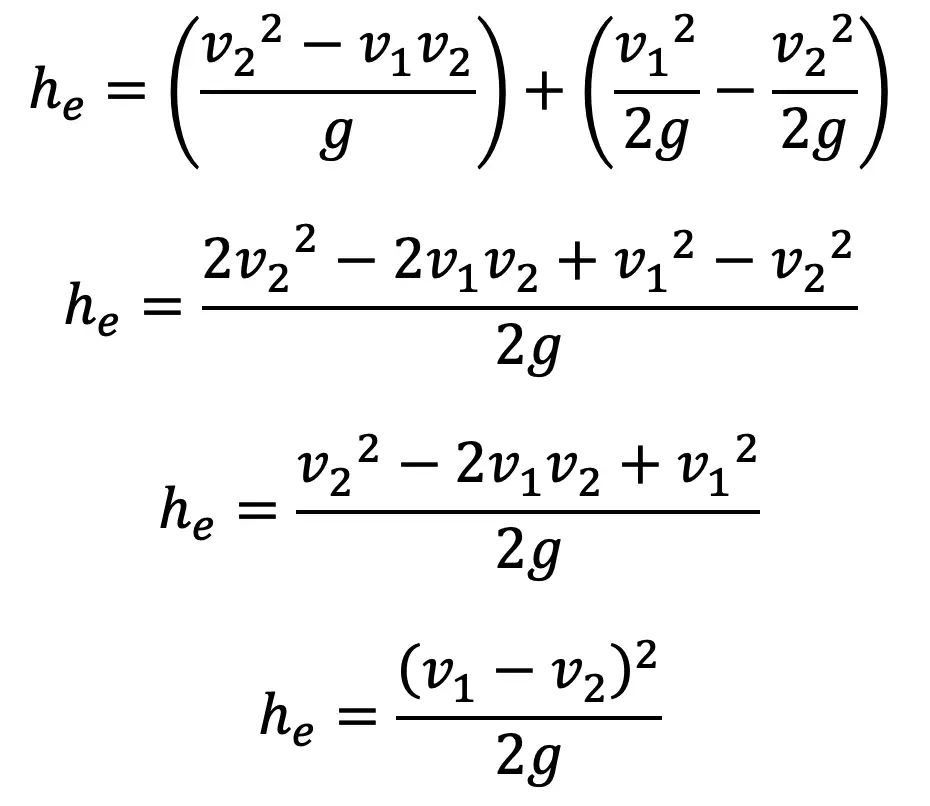
2. Loss of Head due to Sudden Contraction

Consider a liquid flowing in a pipe which has a sudden contraction in the area as shown in the following figure. Consider two sections 1-1 and 2-2 before and after contraction. As the liquid flows from a large pipe to a smaller pipe, the area of flow goes on decreasing and becomes minimum at a section C-C as shown in the following figure.

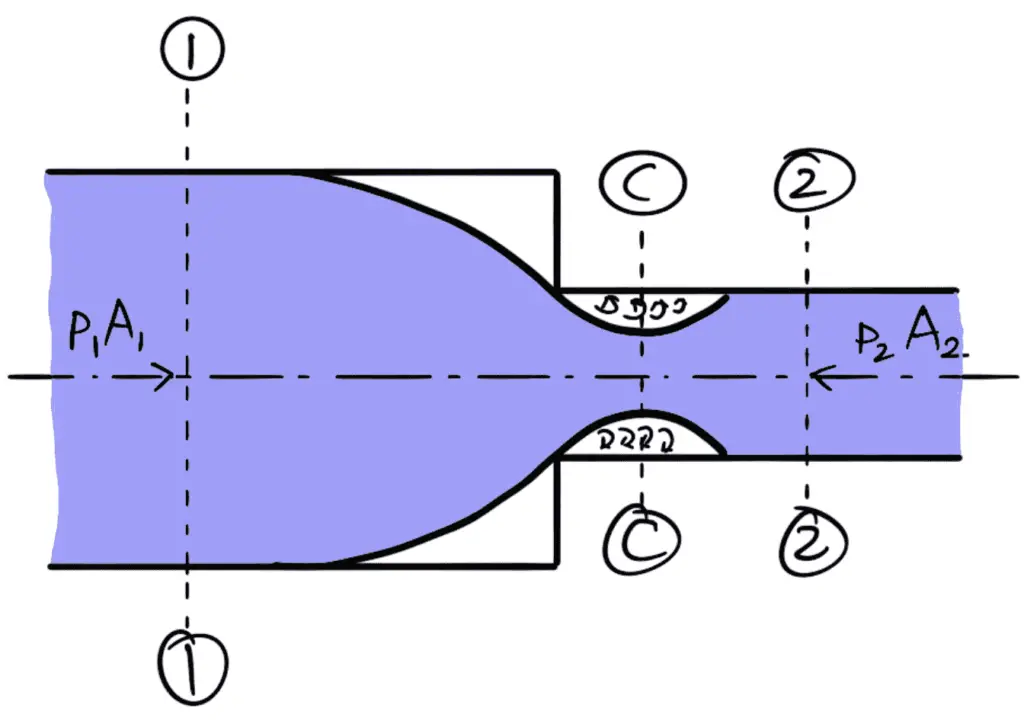
This section C-C is called Vena-contracta. After sections C-C, a sudden enlargement of the area takes place. The loss of the head due to sudden contraction is actually due to sudden enlargement from Vena-contracta to a smaller pipe.

A_c = Area of flow at sections C-C
Vc = Velocity of flow at sections C-C
A₂ = Area of flow at section 2-2
V₂ = Velocity of flow at sections 2-2
h_c = Loss of head due to a sudden contraction

Now h_c = actual loss of head due to enlargement from section C-C to section 2-2 and is given by equation (f) as

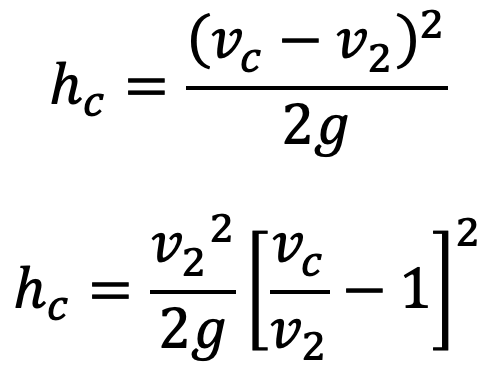
From the continuity equation, we have

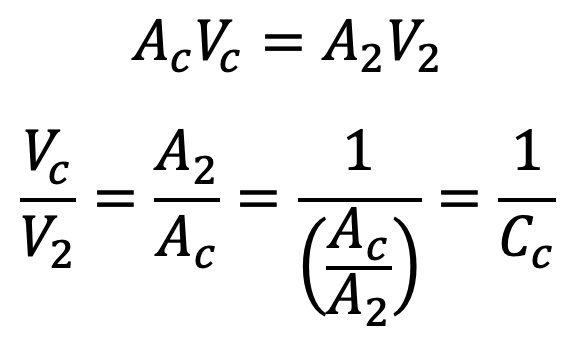
Substituting the value in the equation (g) we get

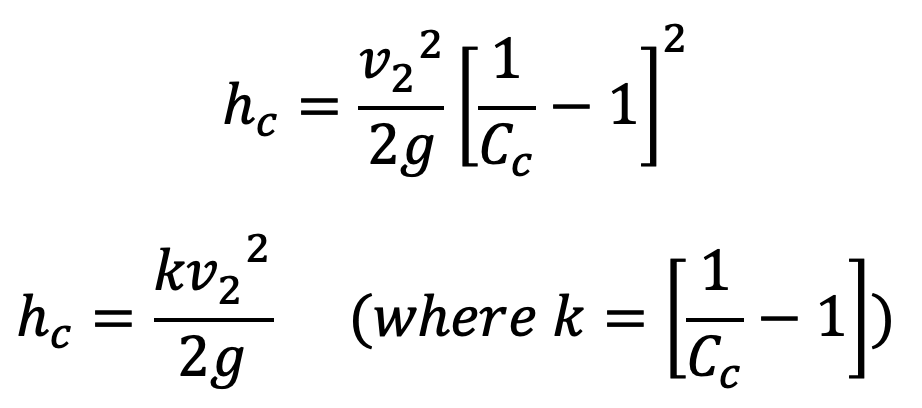
If the value of C_c is assumed to be equal to 0.62, then

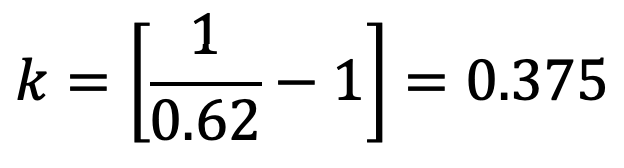
Then h_c, becomes as

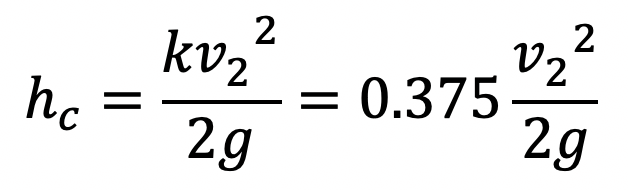
If the value of C_c is not given then the head loss due to contraction is taken as

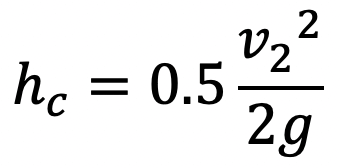
3. Loss of Head at the Entrance of a Pipe

This is the loss of energy which occurs when a liquid enters a pipe which is connected to a large tank or reservoir. This loss is similar to the loss of the head due to sudden contraction. This loss depends on the form of entrance. For a sharp edge entrance, this loss is slightly more than a rounded or bell-mouthed entrance. In practice, the value of loss of head at the entrance (or inlet) of a pipe with a sharp cornered entrance is taken as follows

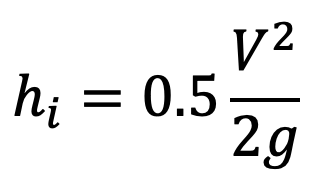
This loss is denoted by h_i

Where V = velocity of liquid in the pipe

4. Loss of Head at the Exit of Pipe

This is the loss of head (or energy) due to the velocity of the liquid at the outlet of the pipe which is dissipated either in the form of a free jet (if the outlet of the pipe is free) or is lost in the tank or reservoir (if the outlet of the pipe is connected to the tank or reservoir). This loss is mentioned below, where V is the velocity of the liquid at the outlet of the pipe. This loss is denoted by h_o

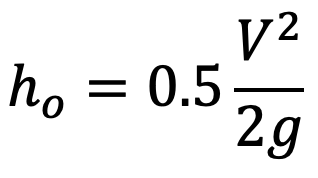
5. Loss of Head Due to an Obstruction in a Pipe

Whenever there is an obstruction in a pipe, the loss of energy takes place due to a reduction of the area of the cross-section of the pipe at the place where the obstruction is present. There is a sudden enlargement of the area of flow beyond the obstruction due to which loss of head takes place as shown in the following figure

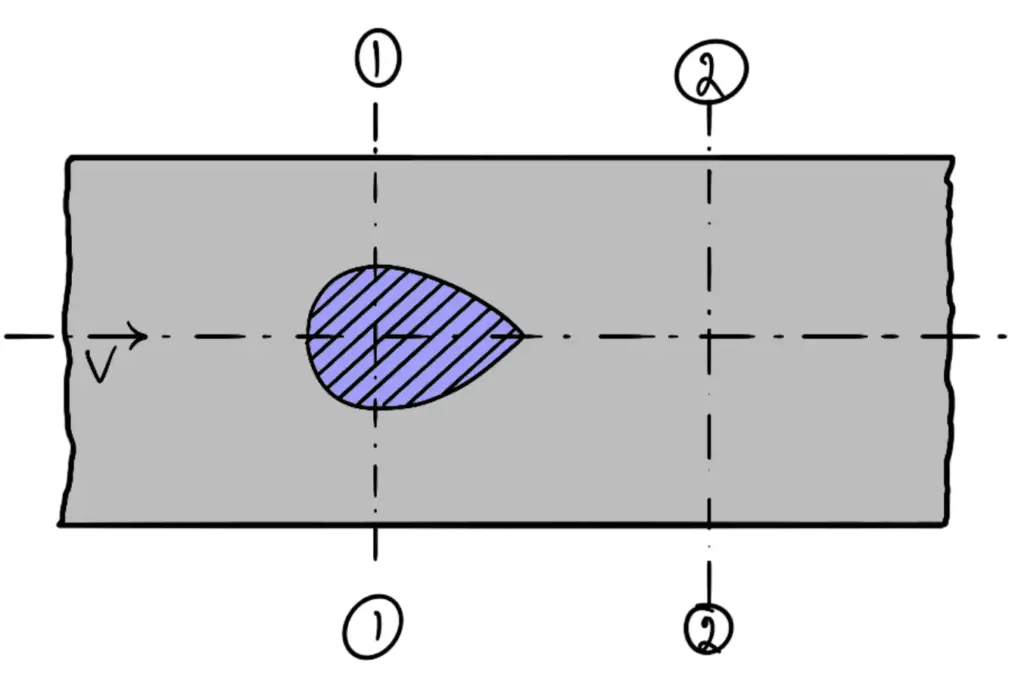
Consider a pipe in the area of cross-section A having an obstruction as shown in the above figure.

Let
a= Maximum area of obstruction
A = Area of pipe
V= Velocity of liquid in the pipe

Then (A – a) = Area of the flow of liquid at section 1-1.

As the liquid flows and passes through section 1-1, a vena-contracta is formed beyond section 1-1, after which the stream of liquid widens again and the velocity of flow at section 2-2 becomes uniform and equal to velocity, V in the pipe. This situation is similar to the flow of liquid through sudden enlargement.

Let V_c = Velocity of liquid at vena-contracta

Then the loss of head due to obstruction = loss of head due to enlargement from vena-contracta to section 2-2.

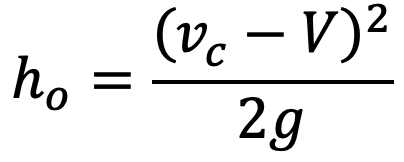
From continuity, we have a_c × V_c = A × V
where a_c = area of cross-section at vena-contracta
If C_c = coefficient of contraction, then

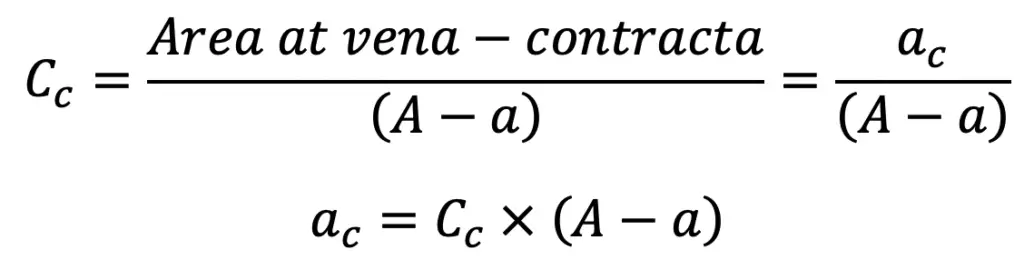
Substituting this value in a_c × V_c = A × V, we get

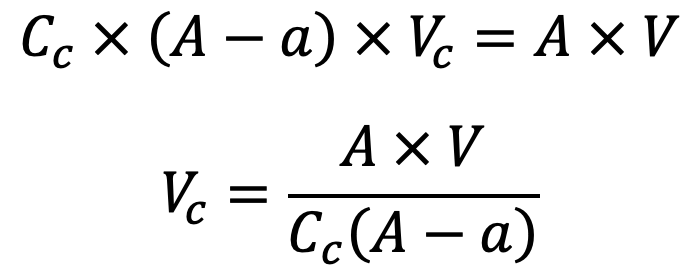
Substituting this value of V_c in equation (j), we get

Head loss due to obstruction can be written as

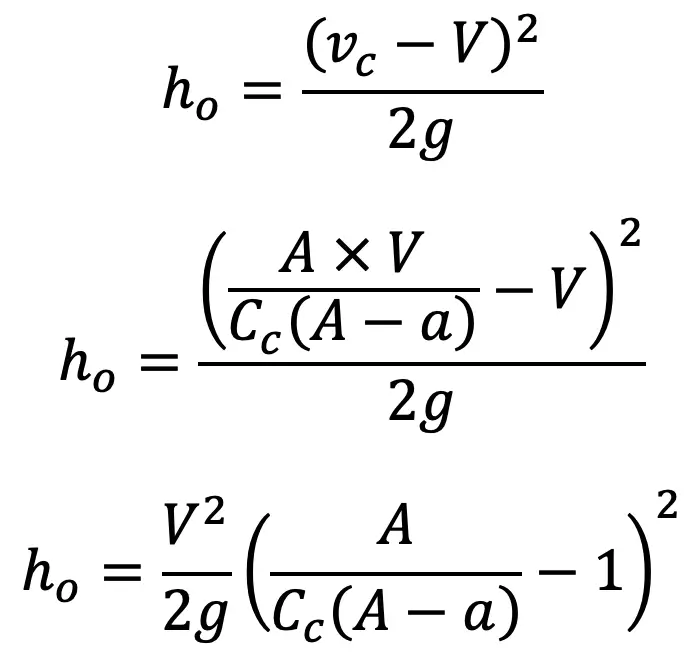
6. Loss of Head due to Bend in Pipe

When there is any bend in a pipe, the velocity of flow changes, due to which the separation of the flow from the boundary and also the formation of eddies takes place. Thus the energy is lost. Loss of head in the pipe due to bend is expressed as

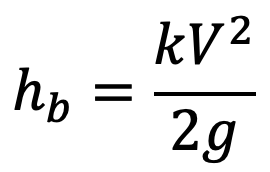
where h_b = loss of head due to bend
V = velocity of flow
k = coefficient of bend

The value of k depends on

• Angle of bend
• The radius of curvature of the bend
• Diameter of pipe

7. Energy Losses in Various Pipe Fittings

The loss of head in the various pipe fittings such as valves, couplings etc., is expressed as

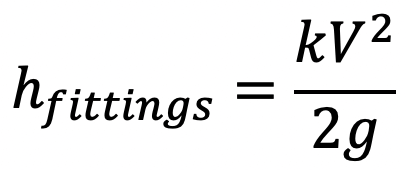
where
V = velocity of flow
k = coefficient of pipe fitting

These are the different Energy losses due to friction and other minor factors in pipes. Let us know what you think about this article in the comment section below.